Catalan数——卡特兰数
今天阿里淘宝笔试中碰到两道组合数学题,感觉非常亲切,但是笔试中失踪推导不出来
后来查了下,原来是Catalan数。悲剧啊,现在整理一下
一、Catalan数的定义令h(1)=1,Catalan数满足递归式:h(n) = h(1)*h(n-1) + h(2)*h(n-2) + ... + h(n-1)h(1),n>=2该递推关系的解为:h(n) = C(2n-2,n-1)/n,n=1,2,3,...(其中C(2n-2,n-1)表示2n-2个中取n-1个的组合数)
问题描述:
12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
这个笔试题,很YD,因为把某个递推关系隐藏得很深。
问题分析:
我们先把这12个人从低到高排列,然后,选择6个人排在第一排,那么剩下的6个肯定是在第二排.
用0表示对应的人在第一排,用1表示对应的人在第二排,那么含有6个0,6个1的序列,就对应一种方案.
比如000000111111就对应着
第一排:0 1 2 3 4 5
第二排:6 7 8 9 10 11
010101010101就对应着
第一排:0 2 4 6 8 10
第二排:1 3 5 7 9 11
问题转换为,这样的满足条件的01序列有多少个。
观察1的出现,我们考虑这一个出现能不能放在第二排,显然,在这个1之前出现的那些0,1对应的人
要么是在这个1左边,要么是在这个1前面。而肯定要有一个0的,在这个1前面,统计在这个1之前的0和1的个数。
也就是要求,0的个数大于1的个数。
OK,问题已经解决。
如果把0看成入栈操作,1看成出栈操作,就是说给定6个元素,合法的入栈出栈序列有多少个。
这就是catalan数,这里只是用于栈,等价地描述还有,二叉树的枚举、多边形分成三角形的个数、圆括弧插入公式中的方法数,其通项是c(2n, n)/(n+1)。
在<<计算机程序设计艺术>>,第三版,Donald E.Knuth著,苏运霖译,第一卷,508页,给出了证明:
问题大意是用S表示入栈,X表示出栈,那么合法的序列有多少个(S的个数为n)
显然有c(2n, n)个含S,X各n个的序列,剩下的是计算不允许的序列数(它包含正确个数的S和X,但是违背其它条件)。
在任何不允许的序列中,定出使得X的个数超过S的个数的第一个X的位置。然后在导致并包括这个X的部分序列中,以S代替所有的X并以X代表所有的S。结果是一个有(n+1)个S和(n-1)个X的序列。反过来,对一垢一种类型的每个序列,我们都能逆转这个过程,而且找出导致它的前一种类型的不允许序列。例如XXSXSSSXXSSS必然来自SSXSXXXXXSSS。这个对应说明,不允许的序列的个数是c(2n, n-1),因此an = c(2n, n) - c(2n, n-1)。
验证:其中F表示前排,B表示后排,在枚举出前排的人之后,对应的就是后排的人了,然后再验证是不是满足后面的比前面对应的人高的要求。
#include <iostream>
using namespace std;
int bit_cnt(int n)
{
int result = 0;
for (; n; n &= n-1, ++result);
return result;
}
int main(void)
{
int F[6], B[6];
int i,j,k,state,ok,ans = 0;
for (state = 0; state < (1 << 12); ++state)
{
if (bit_cnt(state) == 6)
{
i = j = 0;
for (int k = 0; k < 12; ++k)
{
if(state&(1<<k))
F[i++] = k;
else
B[j++] = k;
}
ok = 1;
for (k = 0; k < 6; ++k)
{
if (B[k] < F[k])
{
ok = 0;
break;
}
}
ans += ok;
}
}
cout << ans << endl;
return 0;
}
结果:132
而c(12, 6)/7 = 12*11*10*9*8*7/(7*6*5*4*3*2) = 132
注意:c(2n, n)/(n+1) = c(2n, n) - c(2n, n-1)
估计出题的人也读过<<计算机程序艺术>>吧。
PS:
另一个很YD的问题:
有编号为1到n(n可以很大,不妨在这里假定可以达到10亿)的若干个格子,从左到右排列。
在某些格子中有一个棋子,不妨设第xi格有棋子(1<=i<=k, 1<=k<=n)
每次一个人可以把一个棋子往左移若干步,但是不能跨越其它棋子,也要保证每个格子至多只有一个棋子。
两个人轮流移动,移动不了的为输,问先手是不是有必胜策略。
三、Catalan数的典型应用:
1、括号化问题。矩阵链乘: P=A1×A2×A3×……×An,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?
一个有n个X和n个Y组成的字串,且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:
XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY
将上例的X换成左括号,Y换成右括号,Cn表示所有包含n组括号的合法运算式的个数:
((())) ()(()) ()()() (())() (()())
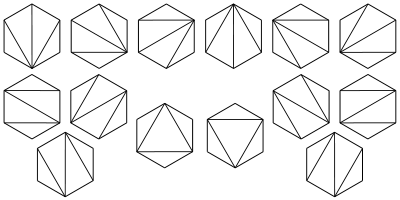
2、将多边行划分为三角形问题。将一个凸多边形区域分成三角形区域(划分线不交叉)的方法数?
类似:在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
3、出栈次序问题。一个栈(无穷大)的进栈序列为1、2、3、...、n,有多少个不同的出栈序列?
类似:有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)
类似:一位大城市的律师在他住所以北n个街区和以东n个街区处工作,每天她走2n个街区去上班。如果他从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
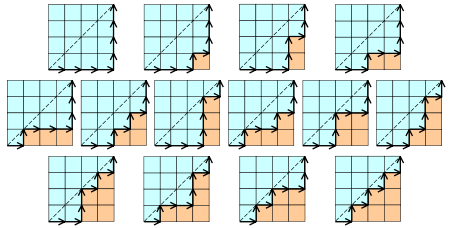
分析:对于每一个数来说,必须进栈一次、出栈一次。我们把进栈设为状态‘1’,出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b),因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数的方案种数。
给定N个节点,能构成多少种形状不同的二叉树?
(一定是二叉树!先取一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) + ...... + h(n-1)h(0)=h(n)) (能构成h(N)个)

在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求(由左而右扫描,0的累计数大于1的累计数)的方案数即为所求。
不符合要求的数的特征是由左而右扫描时,必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数,此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换,使之成为n-m个0和n-m-1个1,结果得1个由n+1个0和n-1个1组成的2n位数,即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。
反过来,任何一个由n+1个0和n-1个1组成的2n位二进制数,由于0的个数多2个,2n为偶数,故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换,使之成为由n个0和n个1组成的2n位数,即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。
因而不合要求的2n位数与n+1个0,n-1个1组成的排列一一对应。
显然,不符合要求的方案数为c(2n,n+1)。由此得出输出序列的总数目=c(2n,n)-c(2n,n+1)=1/(n+1)*c(2n,n)。
(这个公式的下标是从h(0)=1开始的)