题意:
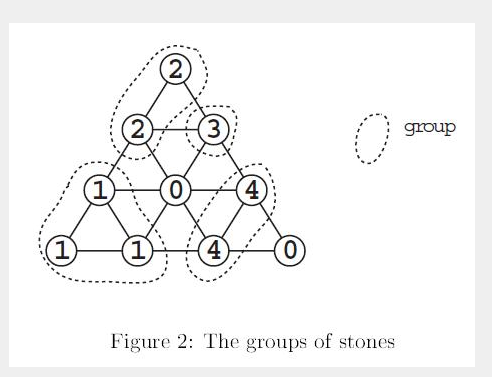
给定一块正三角形棋盘,然后给定一些棋子和空位,棋子序号为a(1<=a<=9),group的定义是相邻序号一样的棋子。
然后到C(1<=N<=9)棋手在空位放上自己序号C的棋子, 放完后, 不与空位相邻的group被消去, 每消去一个不是C的棋子得一分, 消去C的棋子扣一分, 问能得到最多的分数是多少。
分析:
令ans = 0;
搜索每一个棋子, 找出他的group。
如果这个group不与空位相邻, 而且棋子与棋手序号相等, 那么ans -= group数量, 如果棋子不与棋手序号相等 ans += group数量
可以不设置全局变量来找出搜索块的数量
代码:
1 #include <cstdio> 2 #include <cstring> 3 #include <ios> 4 using namespace std; 5 const int maxn = 15; 6 int N, C; 7 int dir[6][2] = { {-1, 0},{-1, -1},{0, -1},{0, 1},{1, 0},{1, 1} }; 8 bool vis[maxn][maxn]; 9 int board[maxn][maxn]; 10 bool conetZero = 0; 11 int dfs(int x, int y, int c) 12 { 13 if(board[x][y] == 0) 14 { 15 conetZero = 1; 16 return 0; 17 } 18 vis[x][y] = 1; 19 int cnt = 1; 20 for(int d = 0; d < 6; d++) 21 { 22 int tx = x, ty = y; 23 tx += dir[d][0], ty += dir[d][1]; 24 if(tx <= 0 || tx > N || ty <= 0 || ty > tx || vis[tx][ty]) 25 continue; 26 if(board[tx][ty] == c || board[tx][ty] == 0) 27 cnt += dfs(tx,ty, c); 28 } 29 return cnt; 30 } 31 int solve() 32 { 33 memset(vis, 0 , sizeof(vis)); 34 int ans = 0; 35 36 for(int i = 1; i <= N; i++) 37 for(int j = 1; j <= i; j++) 38 { 39 if(board[i][j] != 0 && !vis[i][j]) 40 { 41 conetZero = 0; 42 int temp = dfs(i,j,board[i][j]); 43 if(!conetZero){ 44 ans += board[i][j] == C ? -temp: temp; 45 } 46 } 47 } 48 return ans; 49 } 50 int main() 51 { 52 while(~scanf("%d %d", &N, &C) && N) 53 { 54 55 memset( board , 0 , sizeof(board) ); 56 57 for(int i = 1; i <= N; i++) 58 for(int j = 1; j <= i; j++) 59 scanf("%d", &board[i][j] ); 60 61 62 63 int ans = -123456; 64 65 for(int i = 1; i <= N; i++) 66 for(int j = 1; j <= i; j++) 67 { 68 if( board[i][j] == 0){ 69 board[i][j] = C; 70 ans = max( ans, solve() ); 71 board[i][j] = 0; 72 } 73 } 74 75 printf("%d ", ans); 76 77 } 78 return 0; 79 }