次短路
次短路的概念其实很简单,我们都知道可以使用Dijkstra、SPFA等求一个点到图中其他点的最短路,而次短路就是除了最短路第二短的路
我们的思路还是使用Dijkstra+堆优化,最短路的基础上,次短路可以由次短路+边更新,也可以由最短路+边 跟新,这里注意一点,因为次短路更新时也会对其它次短路产生影响,所以更新次短路时也需要入队,我们先尝试更新最短路,成功的话就把原来的最短路给次短路,不成功的话就单独尝试更新次短路
例题
https://www.luogu.com.cn/problem/P2865
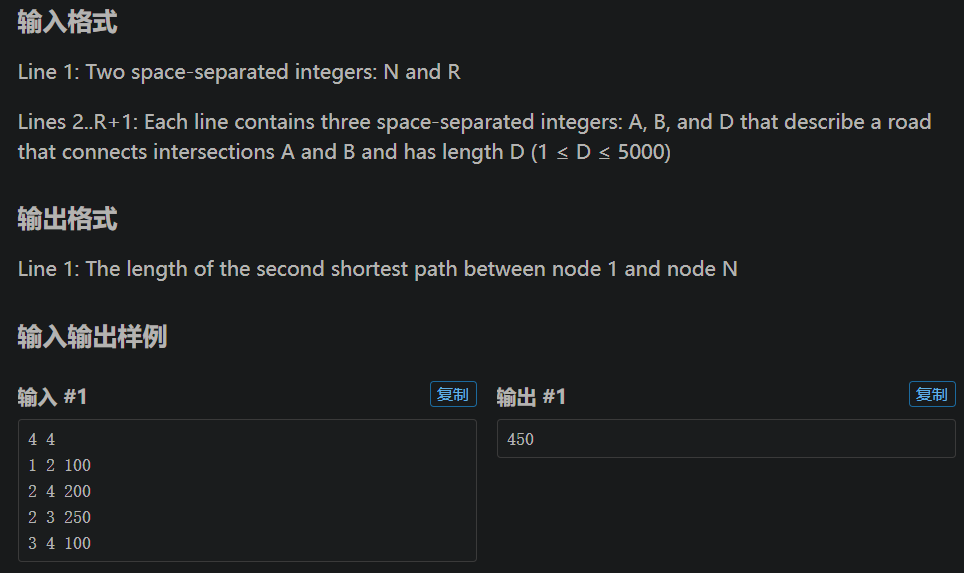
贝茜把家搬到了一个小农场,但她常常回到FJ的农场去拜访她的朋友。贝茜很喜欢路边的风景,不想那么快地结束她的旅途,于是她每次回农场,都会选择第二短的路径,而不象我们所习惯的那样,选择最短路。 贝茜所在的乡村有R(1<=R<=100,000)条双向道路,每条路都联结了所有的N(1<=N<=5000)个农场中的某两个。贝茜居住在农场1,她的朋友们居住在农场N(即贝茜每次旅行的目的地)。 贝茜选择的第二短的路径中,可以包含任何一条在最短路中出现的道路,并且,一条路可以重复走多次。当然咯,第二短路的长度必须严格大于最短路(可能有多条)的长度,但它的长度必须不大于所有除最短路外的路径的长度。
分析
在Dijkstra的基础上,我们将dis一维数组改为dis【maxn】【2】二维数组,dis【maxn】【0】表示最短路,dis【maxn】【1】表示次短路,同时将vis访问标记数组也修改为二维
代码
#include<iostream> #include<cstdio> #include<algorithm> #include<queue> #include<string> #include<cstring> #include<cmath> using namespace std; int n, r,s=1; #define maxn 5001 #define maxm 100001 #define inf 0x3f3f3f3f struct edge { int to; int dis; int next; }e [maxm*2]; //注意这里!!本题的路径是双向的,所以它的邻接表的大小要在maxm的基础上乘2,不然会RE struct node { int dis; int pos; int kind; bool operator <(const node &x)const { return dis > x.dis; } }; int head[maxn], dis[maxn][2], vis[maxn][2],cnt=0; priority_queue<node>q; void addedge(int u,int v, int w) { cnt++; e[cnt].to = v; e[cnt].dis = w; e[cnt].next = head[u]; head[u] = cnt; } void Dijkstra() { memset(vis, 0, sizeof(vis)); memset(dis, inf, sizeof(dis)); dis[s][0] = 0;//dis的初始化 q.push({dis[s][0],s,0}); while (!q.empty()) { int x = q.top().pos; int kind = q.top().kind; q.pop(); if (vis[x][kind])continue; vis[x][kind] = 1; for (int i = head[x]; i; i = e[i].next) { int y = e[i].to; if (dis[y][0] > dis[x][kind] + e[i].dis)//dis[x][kind] + e[i].dis是我们试探的x节点是否能缩短起点到y节点的距离,如果dis[y][0] > dis[x][kind] + e[i].dis表示能将距离缩短 { dis[y][1] = dis[y][0];//将此时的最短路更新为次短路 q.push({ dis[y][1] ,y,1});//入队 dis[y][0] = dis[x][kind] + e[i].dis;//将更短的更新为最短路 q.push({ dis[y][0] ,y,0 });//入队 } else if (dis[y][1] > dis[x][kind] + e[i].dis)//如果只是比次短路短,那么只更新次短路 { dis[y][1] = dis[x][kind] + e[i].dis; q.push({ dis[y][1] ,y,1 }); } } } } int main() { scanf("%d%d", &n, &r); int a, b, c; for (int i = 0; i < r; i++) { scanf("%d%d%d", &a, &b, &c); addedge(a, b, c);//两个:双向路 addedge(b, a, c); } Dijkstra(); printf("%d", dis[n][1]); }
第K短路
同理,第K短路的意思就是输出第K短路的长度
算法——A*
A* 算法(这里的* 英文就读作star),是一种启发式搜索的方法,它离我们并不遥远,常用的BFS就是A*算法的一种特例。
为启发式算法中很重要的一种,被广泛应用在最优路径求解和一些策略设计的问题中。而A*算法最为核心的部分,就在于它的一个估值函数的设计上:
f(n)=g(n)+h(n)
其中f(n)是每个可能试探点的估值,它有两部分组成:一部分为g(n),它表示从起始搜索点到当前点的代价(通常用某结点在搜索树中的深度来表示)。另一部分,即h(n),它表示启发式搜索中最为重要的一部分,即当前结点到目标结点的估值,h(n)设计的好坏,直接影响着具有此种启发式函数的启发式算法的是否能称为A*算法。
在使用A*算法进行解题的时候,我们将起始点到图中的某一点的距离作为g函数,将该某一点到终点的距离作为h函数
g函数的计算:我们使用简单的BFS进行正向的计算
h函数的计算:我们使用Dijkstra算法进行反向图的距离计算:这里如果是单向图,我们就要建立反向图,如果是双向图的话就不用了,直接在原图求到终点的距离就行。
上面例题的A*代码
#include<iostream> #include<cstdio> #include<queue> #include<string> #include<cstring> #include<algorithm> using namespace std; #define inf 0x3f3f3f3f #define maxn 5001 #define maxm 100001 struct edge { int to; int dis; int next; }e[maxm*2],e2[maxm*2];//注意如果是双向路的话要*2!!!! struct node//A*算法中使用 { int dis;//正向图起始点到该点的距离 int pos;//下标 int h;//反向图中该点到重点的e距离 bool operator<(const node& x)const { if (dis + h == x.dis + x.h)return dis>x.dis; else return dis + h > x.dis + x.h; } }; struct node2//Dijkstra中使用 { int dis; int pos; bool operator<(const node2& x)const { return dis > x.dis; } }; int head[maxn],head2[maxn], cnt = 0,cnt2=0, vis[maxn],dis[maxn]; int n, m, t, s,k; void addedge(int u,int v,int w)//正向图 { cnt++; e[cnt].to = v; e[cnt].dis = w; e[cnt].next = head[u]; head[u] = cnt; } void addedge2(int u, int v, int w)//反向图 { cnt2++; e2[cnt2].to = v; e2[cnt2].dis = w; e2[cnt2].next = head2[u]; head2[u] = cnt2; } void Dijkstra() { memset(dis, inf, sizeof(dis)); dis[t] = 0; priority_queue<node2>q; q.push({0, t}); while (!q.empty()) { int x = q.top().pos; q.pop(); if (vis[x])continue; vis[x] = 1; for (int i = head2[x]; i; i = e2[i].next) { int y = e2[i].to; if (dis[y] > dis[x] + e2[i].dis) { dis[y] = dis[x] + e2[i].dis; q.push({dis[y],y}); } } } } int astar(int s, int t, int k)//S起点 t终点 k 第k短 { if (dis[s] ==inf)return -1; if (s == t)k++;//这里kjwyi的原因是如果起点与终点相同的话,意思就是出发最后返回到原点,我们要避免距离为0的情况 priority_queue<node>q; q.push({0,s,dis[s]}); int amount = 0;//出队的次数(队列已经进行了大小的排序,第k次出队就是第k短的路) while (!q.empty()) { int x = q.top().pos; int len = q.top().dis; q.pop(); if (x == t)amount++;//最后x为终点表示已经导论路径终点,此条路径长度已经计算完毕结束 if (amount == k)return len; for (int i = head[x]; i; i = e[i].next) { int y = e[i].to; q.push({len+e[i].dis,y,dis[y]});//一个简单的BFS } } return -1; } int main() { scanf("%d%d", &n, &m); for (int i = 0; i < m; i++) { int a, b, c; scanf("%d%d%d", &a, &b, &c); addedge(a, b, c);//双向图 addedge(b,a, c); addedge2(b, a, c); addedge2(a,b, c); } //scanf("%d%d%d", &s, &t, &k); s = 1; t = n; k = 2; Dijkstra(); printf("%d ", astar(s, t, k)); } //5 5 //1 2 5 //2 3 5 //3 4 4 //4 5 6 //1 5 21 //21
例题2
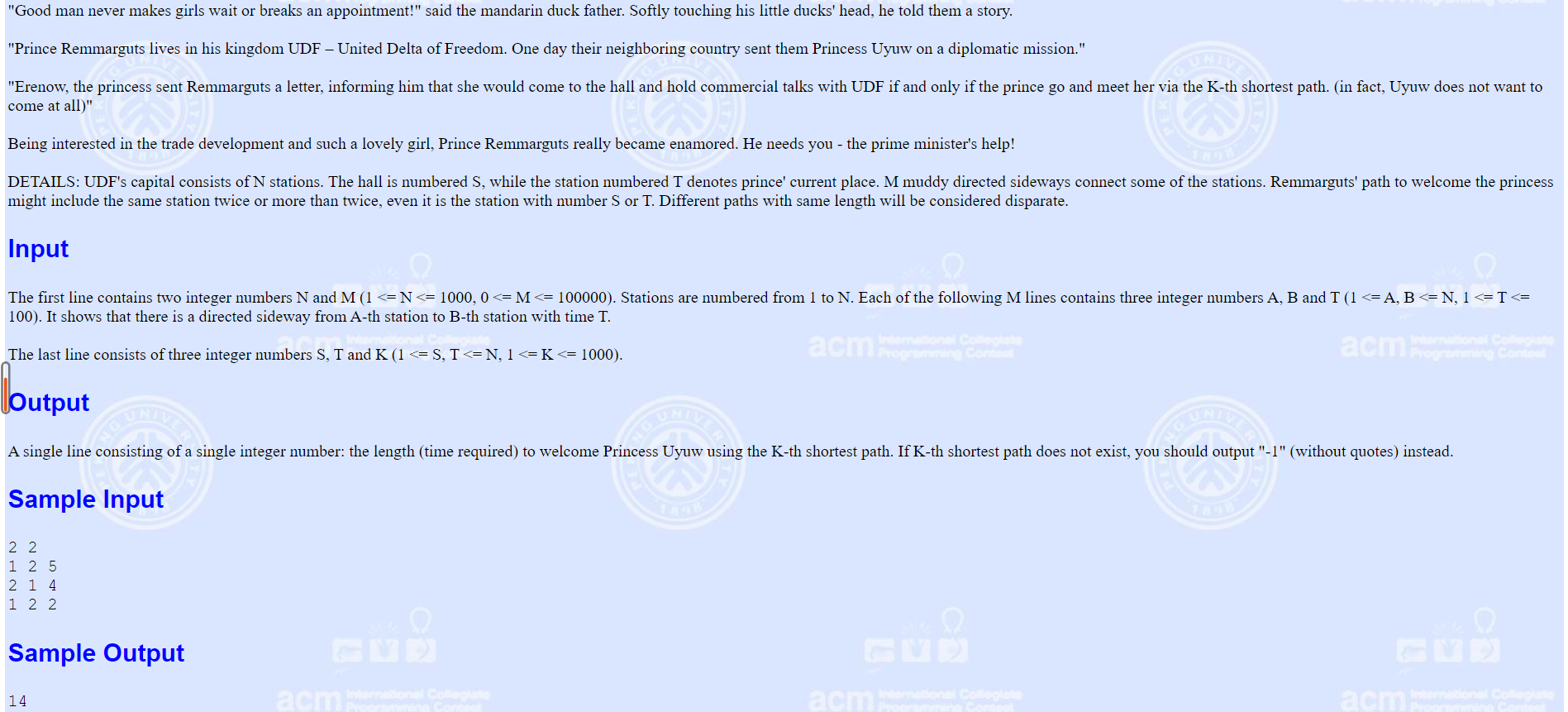
http://poj.org/problem?id=2449
代码
#include<iostream> #include<cstdio> #include<queue> #include<string> #include<cstring> #include<algorithm> using namespace std; #define inf 0x3f3f3f3f #define maxn 1001 #define maxm 100001 struct edge { int to; int dis; int next; }e[maxm],e2[maxm]; struct node { int dis; int pos; int h; bool operator<(const node& x)const { if (dis + h == x.dis + x.h)return dis>x.dis; else return dis + h > x.dis + x.h; } }; struct node2 { int dis; int pos; bool operator<(const node2& x)const { return dis > x.dis; } }; int head[maxn],head2[maxn], cnt = 0,cnt2=0, vis[maxn],dis[maxn]; int n, m, t, s,k; void addedge(int u,int v,int w) { cnt++; e[cnt].to = v; e[cnt].dis = w; e[cnt].next = head[u]; head[u] = cnt; } void addedge2(int u, int v, int w) { cnt2++; e2[cnt2].to = v; e2[cnt2].dis = w; e2[cnt2].next = head2[u]; head2[u] = cnt2; } void Dijkstra() { memset(dis, inf, sizeof(dis)); dis[t] = 0; priority_queue<node2>q; q.push({0, t}); while (!q.empty()) { int x = q.top().pos; q.pop(); if (vis[x])continue; vis[x] = 1; for (int i = head2[x]; i; i = e2[i].next) { int y = e2[i].to; if (dis[y] > dis[x] + e2[i].dis) { dis[y] = dis[x] + e2[i].dis; q.push({dis[y],y}); } } } } int astar(int s, int t, int k) { if (dis[s] ==inf)return -1; if (s == t)k++; priority_queue<node>q; q.push({0,s,dis[s]}); int amount = 0; while (!q.empty()) { int x = q.top().pos; int len = q.top().dis; q.pop(); if (x == t)amount++; if (amount == k)return len; for (int i = head[x]; i; i = e[i].next) { int y = e[i].to; q.push({len+e[i].dis,y,dis[y]}); } } return -1; } int main() { scanf("%d%d", &n, &m); for (int i = 0; i < m; i++) { int a, b, c; scanf("%d%d%d", &a, &b, &c); addedge(a, b, c); addedge2(b, a, c); } scanf("%d%d%d", &s, &t, &k); Dijkstra(); printf("%d ", astar(s, t, k)); }