问题来源:在经典的机器学习中,我们往往假设训练集和测试集分布一致,但是在实际的问题中,测试环境往往与训练的数据有较大的差异,出现过拟合问题:在训练集上训练结构较好,但是在测试集上的效果不好,因此出现了迁移学习技术。
分布不一致的理解:

领域自适应(Domain Adaptation)
是迁移学习(Transfer Learning)的一种,思路是将不同领域(如两个不同的数据集)的数据特征映射到同一个特征空间,这样可利用其它领域数据来增强目标领域训练。
领域自适应(Domain Adaptation)是迁移学习中的一种代表性方法,指的是利用信息丰富的源域样本来提升目标域模型的性能。
源域(source domain):与测试样本不同的领域,但是有丰富的监督信息
目标域(target domain):测试样本所在的领域,无标签或者只有少量标签
源域和目标域往往属于同一类任务,但是分布不同。
领域适应学习的使用场景:无监督的,有监督的,异构分布和多个源域问题。
三种不同的领域自适应方法:
样本自适应:其基本思想是对源域样本进行重采样,从而使得重采样后的源域样本和目标域样本分布基本一致,在重采样的样本集合上重新学习分类器。(适用于源于和目标域分布差异小的情况)
理解:就是在源域中有一些样本与目标域的样本相似,在训练源域中的样本的时候乘以一个权重,即与目标域越相似,则该权重越大
特征自适应:其基本思想是学习公共的特征表示,在公共特征空间,源域和目标域的分布要尽可能相同。(适用于对源域和目标域有一定差异的情况)
理解:通过一个映射使源域样本与目标样本调整到同一个特征空间
模型自适应:其基本思想是直接在模型层面进行自适应。模型自适应的方法有两种思路,一是直接建立模型,但是在模型中加入“domain间距离近”的约束,二是采用迭代的方法,渐进地对目标域的样本进行分类,将信度高的样本加入训练集,并更新模型。(适用于源域和目标域差异比较大的情况)
理解:在无监督的自适应中,使用衡量源域和目标域数据的距离的数学公式作为LOSS进行训练,使得距离缩小。
衡量源域和目标域数据的距离的数学公式:
KL Divergence:度量两个函数的相似程度或者相近程度
离散型随机变量:
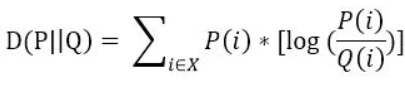
连续型随机变量:

maximum mean discrepancy(最大均值差异MMD):对每一个样本进行投影并求和,利用和的大小表述两个数据的分布差异

原理:一个随机变量的矩反应了对应的分布信息,比如一阶中心矩是均值,二阶中心矩是方差等等
但是均值与方差都相等并不能表示服从一个分布,所以需要更高阶的矩来描述分布
MMD的基本思想就是,如果两个随机变量的任意阶都相同的话,那么两个分布就是一致的。而当两个分布不相同的话,那么使得两个分布之间差距最大的那个矩应该被用来作为度量两个分布的标准。
两个分布应该是由任意阶来描述:高斯核函数对应的映射函数恰好可以映射到无穷维上