误差原因
我们已讨论了一些用于测量模型性能的基本指标,现在来关注一下模型起初为何会出现误差。
在模型预测中,模型可能出现的误差来自两个主要来源,即:因模型无法表示基本数据的复杂度而造成的偏差(bias),或者因模型对训练它所用的有限数据过度敏感而造成的方差(variance)。我们会对两者进行更详细的探讨。

偏差造成的误差 - 准确率和欠拟合
如前所述,如果模型具有足够的数据,但因不够复杂而无法捕捉基本关系,则会出现偏差。这样一来,模型一直会系统地错误表示数据,从而导致准确率降低。这种现象叫做欠拟合(underfitting)。
简单来说,如果模型不适当,就会出现偏差。举个例子:如果对象是按颜色和形状分类的,但模型只能按颜色来区分对象和将对象分类(模型过度简化),因而一直会错误地分类对象。
或者,我们可能有本质上是多项式的连续数据,但模型只能表示线性关系。在此情况下,我们向模型提供多少数据并不重要,因为模型根本无法表示其中的基本关系,我们需要更复杂的模型。

方差造成的误差 - 精度和过拟合
在训练模型时,通常使用来自较大训练集的有限数量样本。如果利用随机选择的数据子集反复训练模型,可以预料它的预测结果会因提供给它的具体样本而异。在这里,方差(variance)用来测量预测结果对于任何给定的测试样本会出现多大的变化。
出现方差是正常的,但方差过高表明模型无法将其预测结果泛化到更多的数据。对训练集高度敏感也称为过拟合(overfitting),而且通常出现在模型过于复杂或我们没有足够的数据支持它时。
通常,可以利用更多数据进行训练,以降低模型预测结果的方差并提高精度。如果没有更多的数据可以用于训练,还可以通过限制模型的复杂度来降低方差。



改进模型的有效性
我们可以看到,在给定一组固定数据时,模型不能过于简单或复杂。如果过于简单,模型无法了解数据并会错误地表示数据。但是,如果建立非常复杂的模型,则需要更多数据才能了解基本关系,否则十分常见的是,模型会推断出在数据中实际上并不存在的关系。
关键在于,通过找出正确的模型复杂度来找到最大限度降低偏差和方差的最有效点。当然,数据越多,模型随着时间推移会变得越好。
要详细了解偏差和方差,建议阅读 Scott Fortmann-Roe 撰写的这篇文章。
除了选定用来训练模型的数据子集外,您使用的哪些来自给定数据集的特征也会显著影响模型的偏差和方差?




学习曲线
让我们根据模型通过可视化图形从数据中学习的能力来探讨偏差与方差之间的关系。
机器学习中的学习曲线是一种可视化图形,能根据一系列训练实例中的训练和测试数据比较模型的指标性能。
在查看数据与误差之间的关系时,我们通常会看到,随着训练点数量的增加,误差会趋于下降。由于我们尝试构建从经验中学习的模型,因此这很有意义。
我们将训练集和测试集分隔开,以便更好地了解能否将模型泛化到未见过的数据而不是拟合到刚见过的数据。
在学习曲线中,当训练曲线和测试曲线均达到稳定阶段,并且两者之间的差距不再变化时,则可以确认模型已尽其所能地了解数据。

理想的学习曲线
模型的最终目标是,误差小并能很好地泛化到未见过的数据(测试数据)。如果测试曲线和训练曲线均收敛,并且误差极低,就能看到这种模型。这种模型能根据未见过的数据非常准确地进行预测。

模型复杂度
与学习曲线图形不同,模型复杂度图形呈现的是模型复杂度如何改变训练曲线和测试曲线,而不是呈现用来训练模型的数据点数量。一般趋势是,随着模型增大,模型对固定的一组数据表现出更高的变化性。

学习曲线与模型复杂度
那么,学习曲线与模型复杂度之间有何关系?
如果我们获取具有同一组固定数据的相同机器学习算法的学习曲线,但为越来越高的模型复杂度创建几个图形,则所有学习曲线图形均代表模型复杂度图形。这就是说,如果我们获取了每个模型复杂度的最终测试误差和训练误差,并依据模型复杂度将它们可视化,则我们能够看到随着模型的增大模型的表现有多好。

模型复杂度的实际使用
既然知道了能通过分析模型复杂度图形来识别偏差和方差的问题,现在可利用一个可视化工具来帮助找出优化模型的方法。在下一部分中,我们会探讨 gridsearch 和如何微调模型以获得更好的性能。
问题 2 - 拟合程度
假设一个数据集有五个数据且一个模型做出下列目标变量的预测:
| 真实数值 | 预测数值 |
|---|---|
| 3.0 | 2.5 |
| -0.5 | 0.0 |
| 2.0 | 2.1 |
| 7.0 | 7.8 |
| 4.2 | 5.3 |
你觉得这个模型已成功地描述了目标变量的变化吗?如果成功,请解释为什么,如果没有,也请给出原因。
提示1:运行下方的代码,使用 performance_metric 函数来计算 y_true 和 y_predict 的决定系数。
提示2: 分数是指可以从自变量中预测的因变量的方差比例。 换一种说法:
为0意味着因变量不能从自变量预测。
为1意味着可以从自变量预测因变量。
在0到1之间表示因变量可预测的程度。
为0.40意味着 Y 中40%的方差可以从 X 预测。
第四步. 分析模型的表现
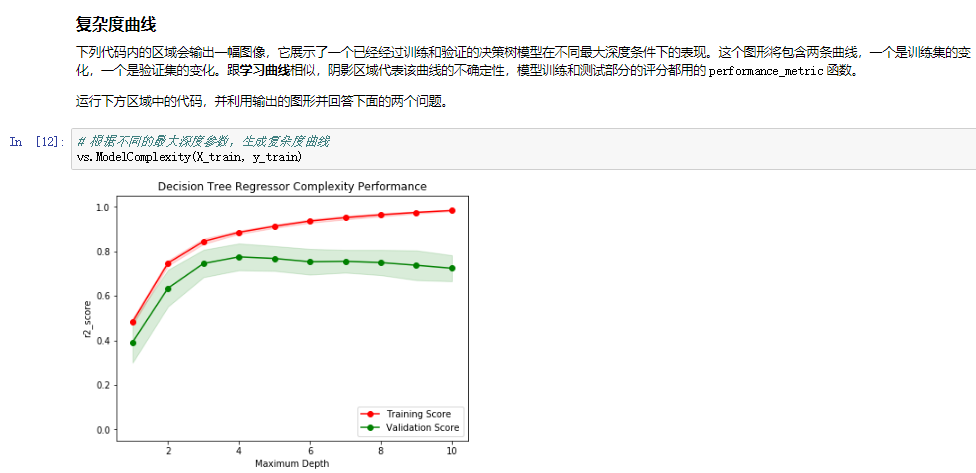
在项目的第四步,我们来看一下不同参数下,模型在训练集和验证集上的表现。这里,我们专注于一个特定的算法(带剪枝的决策树,但这并不是这个项目的重点),和这个算法的一个参数 'max_depth'。用全部训练集训练,选择不同'max_depth' 参数,观察这一参数的变化如何影响模型的表现。画出模型的表现来对于分析过程十分有益,这可以让我们看到一些单看结果看不到的行为。
学习曲线
下方区域内的代码会输出四幅图像,它们是一个决策树模型在不同最大深度下的表现。每一条曲线都直观得显示了随着训练数据量的增加,模型学习曲线的在训练集评分和验证集评分的变化,评分使用决定系数R2。曲线的阴影区域代表的是该曲线的不确定性(用标准差衡量)。
运行下方区域中的代码,并利用输出的图形回答下面的问题。