Connectivity
s-t connectivity problem. Given two node s and t, is there a path between s and t?
(s - t连接问题: 给定两个节点s和t,在s和t之间有路径吗?)
s-t shortest path problem. Given two node s and t, what is the length of the shortest path between s and t?
(s-t最短路径问题: 给定两个节点s和t, s和t之间的最短路径的长度是多少?)
Applications.
- Friendster. (交友网站)
- Maze traversal. (迷宫遍历)
- Kevin Bacon number. (凯文·培根数)
- Fewest number of hops in a communication network. (在一个通信网络中最少的跳转数)
Breadth First Search (广度优先搜索)
BFS intuition. Explore outward from s in all possible directions, adding nodes one "layer" at a time.
(BFS的核心思想: 从s节点向外探索所有可能的方向,一次添加一个“层”节点。)

BFS algorithm.
- L0 = { s }.
- L1 = all neighbors of L0.
- L2 = all nodes that do not belong to L0 or L1, and that have an edge to a node in L1.
- ( L2 = 所有不属于L0或L1的节点,并且与L1中的节点有一条边的节点)
- Li+1 = all nodes that do not belong to an earlier layer, and that have an edge to a node in Li.
- ( Li+1 = 不属于前一层的所有节点,并且与Li中的某个节点有一条边)
Theorem. For each i, Li consists of all nodes at distance exactly i from s. There is a path from s to t iff t appears in some layer.
(定理: <1>对于每一个i, Li由距离s正好i的所有节点组成 <2> 存在一条从s到t的路径当且仅当t出现在某个层中)
Property. Let T be a BFS tree of G = (V, E), and let (x, y) be an edge of G. Then the level of x and y differ by at most 1.
(特性: 设T是G = (V, E)的BFS树,设(x, y)是G的一条边,那么x和y的级别相差不超过1)

Breadth First Search: Analysis
Theorem. The above implementation of BFS runs in O(m + n) time if the graph is given by its adjacency representation.
(定理:如果图是用邻接的方式表示的,那么上述BFS的实现在O(m + n)时间内运行)
Pf.
- Easy to prove O(n^2) running time:
-
at most n lists L[i]
each node occurs on at most one list; for loop runs ≤n times (每个节点最多出现在一个列表上;for循环运行≤n次)
when we consider node u, there are ≤n incident edges (u, v),and we spend O(1) processing each edge (考虑节点u时,有≤n条关联边(u, v),对每条边进行O(1)处理)
-
- Actually runs in O(m + n) time:
- when we consider node u, there are deg(u) incident edges (u, v) //考虑节点u时,存在deg(u)个关联边(u, v)
- total time processing edges is Σu∈V deg(u) = 2m (each edge (u, v) is counted exactly twice)
- (总时间处理边Σu∈V deg(u) = 2m (每条边(u, V)精确计数两次) )
Connected Component
Connected component. Find all nodes reachable from s.
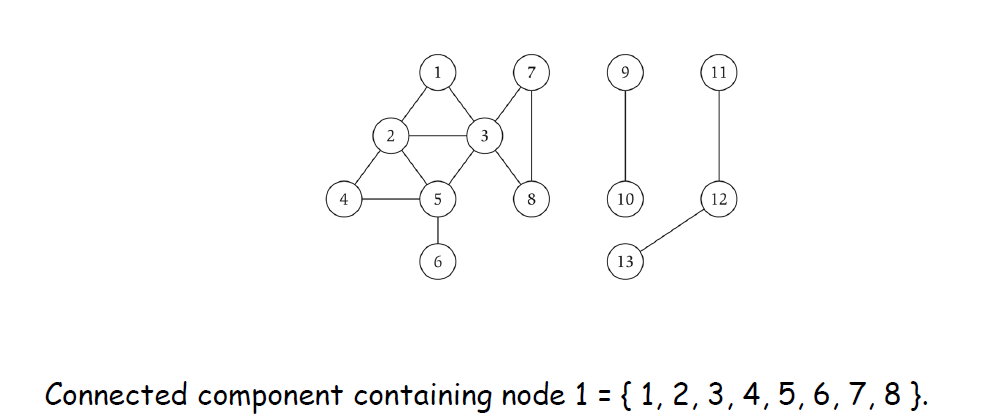

Theorem. Upon termination, R is the connected component containing s. // 在终止时,R是包含s的 "连通组件"
- BFS = explore in order of distance from s. (按距离s的顺序探索)
- DFS = explore in a different way.