队列：最近的请求次数 (Leetcode 933 / Leetcode 232 / 剑指09 / Leetcode 225 / Leetcode 862 )

 

 

 

 

 

 

 

/**
* 暴力解法
* 1.创建数组，存放所有的请求
* 整型数组，存放10000个元素
* 2.把当前请求存入数组
* 记录最后一次存入的索引，从0开始
* 3.统计距离此次请求前3000毫秒之间的请求次数
* 从最后一次存放位置倒序遍历
*
* @param t 时长为 t（单位：毫秒） 的请求
* @return 过去3000毫秒内有多少次请求：[t-3000, t]
*/
public int ping(int t) {
　　// 2.把当前请求存入数组
　　int end = 0;
　　for (int i = 0; i < array.length; i++) {
　　　　if (array[i] == 0) { // 细节：数组元素是0，该位置没有存过请求
　　　　　　array[i] = t;
　　　　　　end = i; // 记录最近一次请求存放的索引
　　　　　　break;
　　　　}
　　}
　　// 3.统计距离此次请求前3000毫秒之间的请求次数
　　int count = 0; // 计数器
　　while (array[end] >= t - 3000) {
　　　　count++;
　　　　if (--end < 0) { // 防止越界
　　　　　　break;
　　　　}
　　}
　　return count; 
}

 

 

 

// 1.创建数组，存放所有的请求
// int[] array = new int[10000];
int[] array = new int[3002];
// 2.记录起止索引，从0开始
int start = 0, end = 0;
/**
* 优化解法：双指针
* 1.创建数组存放请求：int[3002]
* 2.额外定义开始指针
* start=0，end=0，记录起止索引
* 3.存放请求后，更新起止索引
* end++; 从上次的开始索引（start）向后查找
* 直到新的合法的起始位置
* 4.通过end与start差值计算请求次数
*
* @param t 时长为 t（单位：毫秒） 的请求
* @return 过去3000毫秒内有多少次请求：[t-3000, t]
*/
public int ping(int t) {
　　// 3.存放请求后，更新起止索引
　　array[end++] = t; // 存放最近一次请求，结束索引加 1
　　end = end == array.length ? 0 : end; // 越界后，从0开始
　　// 从start位置开始，正向查找符合要求的请求次数
　　while (array[start] < t - 3000) { // 过滤掉所有不符合要求的数据
　　　　start ++;
　　　　start = start == array.length ? 0 : start;
　　}
　　// 4.通过end与start差值计算请求次数
　　if (start > end) { // 请求次数超过数组容量，发生了溢出
　　　　return array.length - (start - end);
　　}
　　// 此时，end为最新一次请求 + 1 的索引，start是3000毫秒前的第一次合法请求索引
　　return end - start;
}

 

 

 

 

 

 

/**
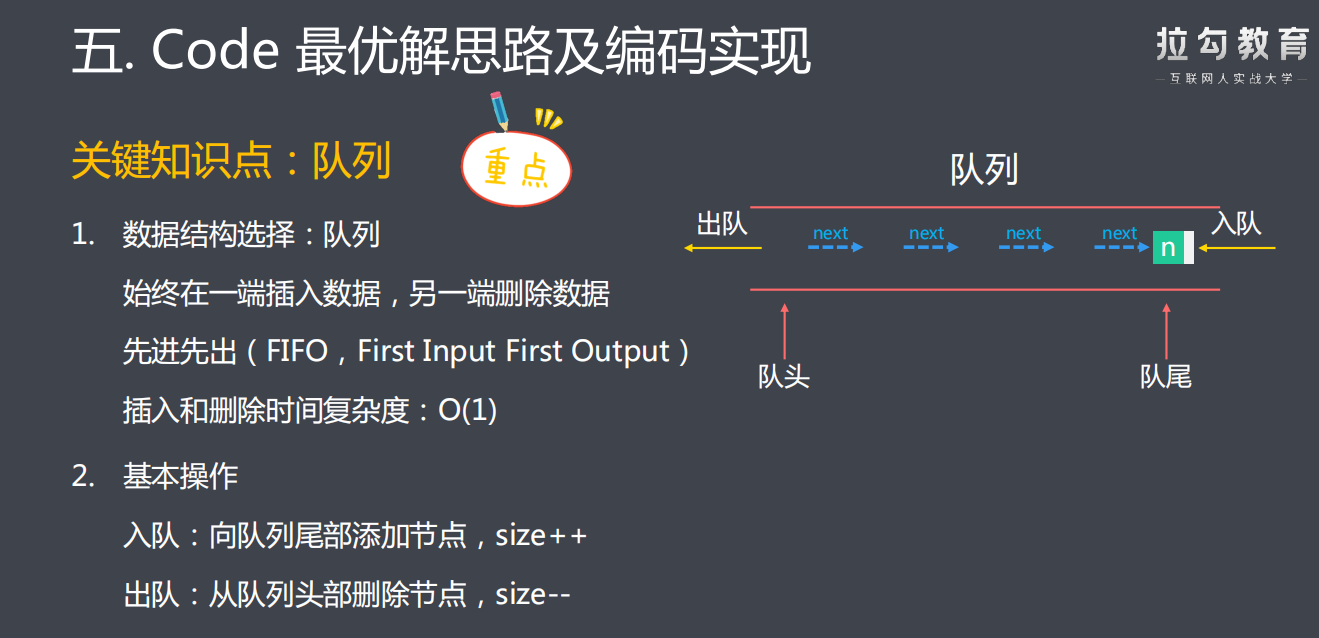
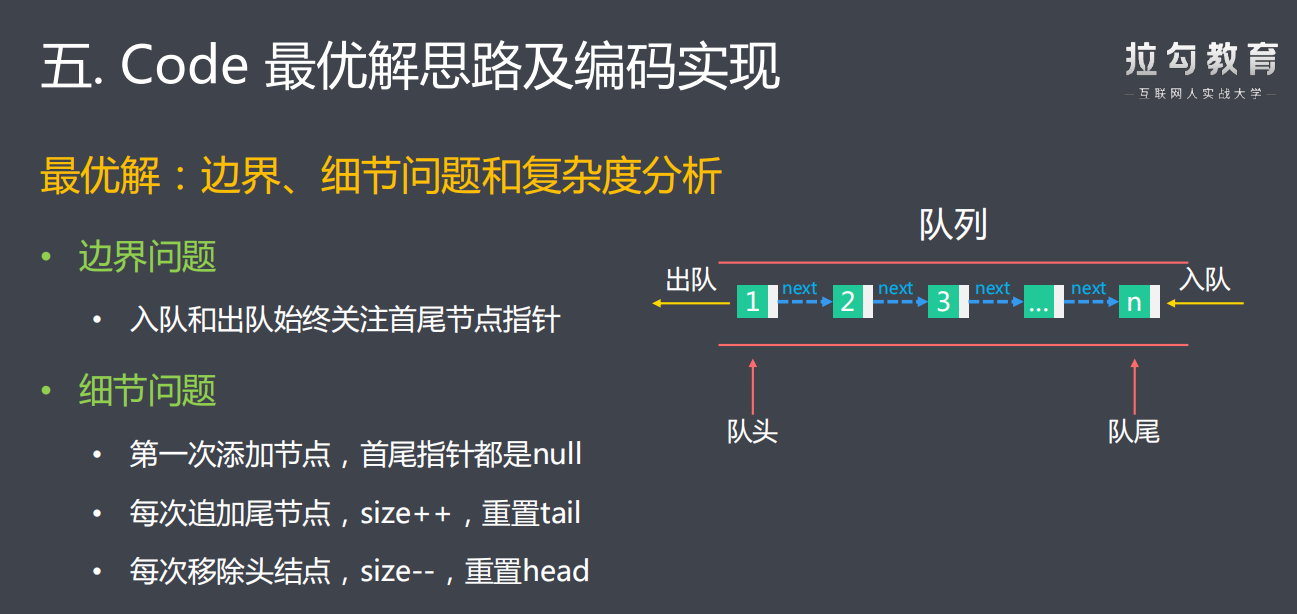
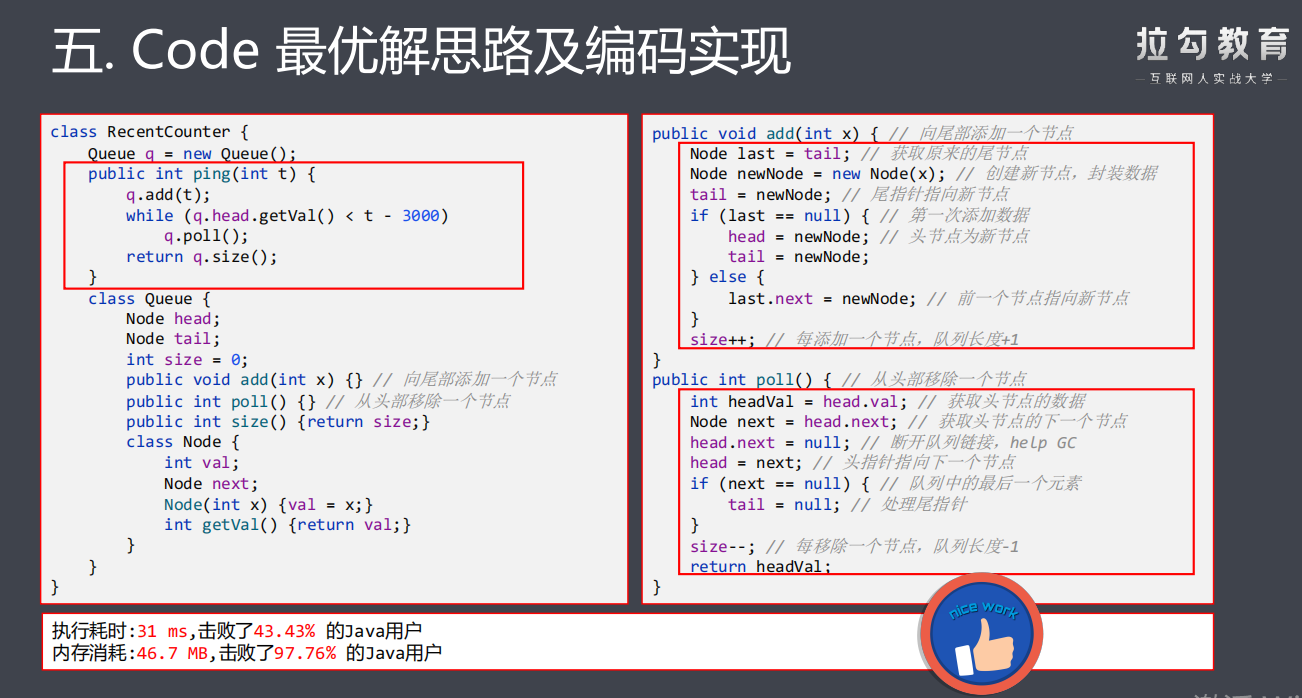
* 最优解：队列解法
* 1.使用链表实现一个队列
* 定义属性：队头-head、队尾-tail、长度-size
* 定义方法：添加节点-add(int)、移除节点-poll() 、队列长度-size()
* 定义内部类：Node，封装每次入队的请求数据和指向下一个节点的指针
* 2.每次请求向队列尾部追加节点
* 3.循环检查队头数据是否合法
* 不合法则移除该节点
* 4.返回队列长度
* @param t
* @return
*/
public int ping(int t) {
　　// 2.每次请求向队列尾部追加节点
　　q.add(t);
　　// 3.循环检查队头数据是否合法
　　while (q.head.getVal() < t - 3000){
　　　　q.poll();
　　}
　　// 4.返回队列长度
　　return q.size();
}

/**
* 最优解：队列解法
* 1.使用链表实现一个队列
* 定义属性：队头-head、队尾-tail、长度-size
* 定义方法：添加节点-add(int)、移除节点-poll() 、队列长度-size()
* 定义内部类：Node，封装每次入队的请求数据和指向下一个节点的指针
* 2.每次请求向队列尾部追加节点
* 3.循环检查队头数据是否合法
* 不合法则移除该节点
* 4.返回队列长度
* @param t
* @return
*/
public int ping(int t) {
　　// 2.每次请求向队列尾部追加节点
　　q.add(t);
　　// 3.循环检查队头数据是否合法
　　while (q.head.getVal() < t - 3000){
　　　　q.poll();
　　}
　　// 4.返回队列长度
　　return q.size();
}

队列实现代码：

Queue q;
public RecentCounter() {
　　q = new Queue();
}
class Queue { // 1.使用链表实现一个队列
　　Node head;
　　Node tail;
　　int size = 0;
　　public Queue() {
　　}
　　public void add(int x) { // 向尾部添加一个节点
　　　　Node last = tail;
　　　　Node newNode = new Node(x);
　　　　tail = newNode; // 尾指针指向新节点
　　　　if (last == null) { // 第一次添加数据
　　　　　　head = newNode;
　　　　　　tail = newNode;
　　　　} else {
　　　　　　last.next = newNode; // 前一个节点指向新节点
　　　　}
　　　　size++; // 每添加一个节点，队列长度+1
　　}
　　public int poll() { // 从头部移除一个节点
　　　　int headVal = head.val; // 获取头节点的数据
　　　　Node next = head.next;
　　　　head.next = null; // 链表第一个节点断开
　　　　head = next; // head指针指向后一个节点
　　　　if (next == null) { // 队列中的最后一个元素
　　　　　　tail = null; // 处理尾指针
　　　　}
　　　　size--; // 每移出一个节点，队列长度减1
　　　　return headVal;
　　}
　　public int size() {
　　　　return size;
　　}
　　class Node { // 队列节点：链表结构
　　　　int val;
　　　　Node next;
　　　　Node(int x) {
　　　　　　val = x;
　　　　}
　　　　int getVal() {
　　　　　　return val;
　　　　}
　　}
}

辅助数据结构：队列。代码如下：

class Queue { // 1.使用链表实现一个队列
　　Node head;
　　Node tail;
　　int size = 0;
　　public Queue() {
　　}
　　public void add(int x) {}
　　public int poll() {}
　　public int size() {}
　　class Node { // 队列节点：链表结构
　　　　int val;
　　　　Node next;
　　　　Node(int x) {
　　　　　　val = x;
　　　　}
　　　　int getVal() {
　　　　　　return val;
　　　　}
　　}
}

输入：inputs = [[1],[100],[3001],[3002]]
输出：[1,2,3,3]

 

 

 1/4 用栈实现队列

  

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列的支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

　　void push(int x) 将元素 x 推到队列的末尾
　　int pop() 从队列的开头移除并返回元素
　　int peek() 返回队列开头的元素
　　boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

　　你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
　　你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

进阶：

　　你能否实现每个操作均摊时间复杂度为 O(1) 的队列？换句话说，执行 n 个操作的总时间复杂度为 O(n) ，即使其中一个操作可能花费较长时间。

示例：

输入：
　　["MyQueue", "push", "push", "peek", "pop", "empty"]
　　[[], [1], [2], [], [], []]
输出：
　　[null, null, null, 1, 1, false]

解释：
　　MyQueue myQueue = new MyQueue();
　　myQueue.push(1); // queue is: [1]
　　myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
　　myQueue.peek(); // return 1
　　myQueue.pop(); // return 1, queue is [2]
　　myQueue.empty(); // return false

提示：

　　1 <= x <= 9
　　最多调用 100 次 push、pop、peek 和 empty
　　假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）

/**
 * 入队（push）:
 * 新元素总是压入 s1 的栈顶，同时我们会把 s1 中压入的第一个元素赋值给作为队首元素的 front 变量
 * 出队（pop）:
 * 根据栈 LIFO 的特性，s1 中第一个压入的元素在栈底。为了弹出 s1 的栈底元素，我们得把 s1 中所有的元素全部弹出，
 * 再把它们压入到另一个栈 s2 中，这个操作会让元素的入栈顺序反转过来。通过这样的方式，s1 中栈底元素就变成了 s2 的栈顶元素，
 * 这样就可以直接从 s2 将它弹出了。一旦 s2 变空了，我们只需把 s1 中的元素再一次转移到 s2 就可以了
 * 
 * 入队 - O(1)，出队 - 摊还复杂度 O(1)
 */
public class MyQueue {
    private Stack<Integer> s1;//入栈
    private Stack<Integer> s2;//出栈
    //构造方法
    public MyQueue(){
        s1 = new Stack<>();
        s2 = new Stack<>();
    }

    //入栈
    public void push(int x) {
    /*
    1.首先给s1入栈
     */
        s1.push(x);
    }

    public int pop() {
    /*
    1.如果s2为空，则将s1(是否为空)全部的值先移动到s2
    2.如果s2有值，则直接弹出
     */
        if (s2.empty()){
            while(!s1.empty()){
                s2.push(s1.pop());
            }
        }
        //这个判断条件就是去除s1为空，从而导致s2也为空的情况
        if (!s2.empty()){
            return s2.pop();
        }
        return -1;
    }

    public int peek() {
        if (s2.empty()){
            while(!s1.empty()){
                s2.push(s1.pop());
            }
        }
        if (!s2.empty()){
            return s2.peek();
        }
        return -1;

    }

    public boolean empty() {
        if (s1.empty() && s2.empty()){
            return true;
        }
        return false;
    }
}


/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = new MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * boolean param_4 = obj.empty();
 */

2/4 用两个栈实现队列

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，

分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

输入：
　　["CQueue","appendTail","deleteHead","deleteHead"]
　　[[],[3],[],[]]
输出：

　　[null,null,3,-1]

示例 2：

输入：
　　["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"]
　　[[],[],[5],[2],[],[]]
输出：

　　[null,-1,null,null,5,2]
提示：

　　1 <= values <= 10000
　　最多会对 appendTail、deleteHead 进行 10000 次调用

// 思路同上一个题
public class CQueue {
    Stack<Integer> stack1;
    Stack<Integer> stack2;

    public CQueue() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }

    public void appendTail(int value) {
        stack1.push(value);
    }

    public int deleteHead() {
        // 如果第二个栈为空,把第一个栈中的数据一次入栈到第二个栈
        if (stack2.isEmpty()) {
            while (!stack1.isEmpty()) {
                stack2.push(stack1.pop());
            }
        }
        //从第二个栈中出数据
        if (stack2.isEmpty()) {
            return -1;
        } else {
            int deleteItem = stack2.pop();
            return deleteItem;
        }
    }
}

3/4 用队列实现栈

使用队列实现栈的下列操作：

　　push(x) -- 元素 x 入栈
　　pop() -- 移除栈顶元素
　　top() -- 获取栈顶元素
　　empty() -- 返回栈是否为空
注意:

　　你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
　　你所使用的语言也许不支持队列。 你可以使用 list 或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。
　　你可以假设所有操作都是有效的（例如, 对一个空的栈不会调用 pop 或者 top 操作）。

/**
 * 入栈操作时，首先获得入栈前的元素个数 n，然后将元素入队到队列，
 * 再将队列中的前 n个元素（即除了新入栈的元素之外的全部元素）依次出队并入队到队列，
 * 此时队列的前端的元素即为新入栈的元素，且队列的前端和后端分别对应栈顶和栈底。
 *
 * 由于每次入栈操作都确保队列的前端元素为栈顶元素，因此出栈操作和获得栈顶元素操作都可以简单实现。
 * 出栈操作只需要移除队列的前端元素并返回即可，获得栈顶元素操作只需要获得队列的前端元素并返回即可（不移除元素）。
 * 由于队列用于存储栈内的元素，判断栈是否为空时，只需要判断队列是否为空即可。
 */

public class MyStack {
    Queue<Integer> queue;

    /** 初始化数据结构. */
    public MyStack() {
        queue = new LinkedList<Integer>();
    }

    public void push(int x) {
        int n = queue.size();
        queue.offer(x);
        for (int i = 0; i < n; i++) {
            queue.offer(queue.poll());
        }
    }

    public int pop() {
        return queue.poll();
    }

    public int top() {
        return queue.peek();
    }

    public boolean empty() {
        return queue.isEmpty();
    }
}

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack obj = new MyStack();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.top();
 * boolean param_4 = obj.empty();
 */

4/4 和至少为 K 的最短子数组

返回 A 的最短的非空连续子数组的长度，该子数组的和至少为 K 。

如果没有和至少为 K 的非空子数组，返回 -1 。

示例 1：

　　输入：　　A = [1], K = 1
　　输出：　　1

示例 2：

　　输入：　　A = [1,2], K = 4
　　输出：　　-1
示例 3：　　

　　输入：　　A = [2,-1,2], K = 3
　　输出：　　3

提示：

　　1 <= A.length <= 50000
　　-10 ^ 5 <= A[i] <= 10 ^ 5
　　1 <= K <= 10 ^ 9

//通过维持一个队列，从头到尾遍历。对于每个y，找出满足，P[y]-P[x]>=K的最大的x。如果y-x比之前的长度要小就记录新的最小值
class Solution {
    //先计算前缀和p数组
    // 通过维持一个队列，从头到尾遍历。对于每个y，找出满足，p[y]-p[x]>=K的最大的x。
    // 计算的就是 ((0...y-1) - (0....x-1) )=(x....y-1)  长度为y-1-x+1=y-x
    // 如果y-x比之前的长度要小就记录新的最小值
    // 细节问题：要注意负数的情况
    public int shortestSubarray(int[] A, int K) {
        int size = A.length;
        long[] p = new long[size + 1]; //前缀和preSum
        //一次累加每一个值 p[y]存放的是 A数组中从0加到y-1位置
        for (int i = 0; i < size; ++i)
            p[i + 1] = p[i] + (long) A[i];

        int result = size + 1;//最小长度
        Deque<Integer> queue = new LinkedList();//存放下标 滑动窗口

        for (int y = 0; y < p.length; y++) {         
            //p[y]表示A[y]之前的数字和（A数组中从0加到y-1位置）
            while (!queue.isEmpty() && p[y] <= p[queue.getLast()]) {//存在负数的情况，在队列尾部删除元素
                queue.removeLast();
            }
            //当前队列头到y的范围内元素和大于K，需要判断是否比之前的长度更小
            while (!queue.isEmpty() && p[y] >= p[queue.getFirst()] + K) {    
                result = Math.min(result, y - queue.removeFirst());
            }
            //加到队列尾部
            queue.addLast(y);
        }

        return result < size + 1 ? result : -1;
    }

    //滑动窗口
    public int shortestSubarray2(int[] A, int K) {
        int size = A.length;
        int left = 0, right = 0; //双指针
        int sum = 0;//当前子序列和
        int result = size + 1;

        while (right < size) {//右指针未到边界
            sum = sum + A[right];//累加

            if (sum <= 0) {//出现负值的情况，双指针都后移到当前右指针的下一个位置
                left = right + 1;
                right = right + 1;
                sum = 0;
                continue;
            }

            int i = right;
            while (A[i] < 0) {//将负数变为0，同时在上一个元素加上这负数
                A[i - 1] += A[i];
                A[i] = 0;
                i--;
            }

            if (sum >= K) {//尝试缩小窗口
                while (left <= right && sum - A[left] >= K) {
                    sum = sum - A[left];
                    left++;
                }

                if (right - left + 1 < result) {
                    result = right - left + 1;
                    if (result == 1) { //最短为1个，发现最短直接返回，提前终止
                        return result;
                    }
                }
            }
            right++;

        }
        return result < size + 1 ? result : -1;
    }
}