AVL树

AVL树

• AVL树是最早发明的自平衡二叉搜索树之一
• 平衡因子（Balance Factor）：某节点的左右子树高度差
• AVL树特点：
  1. 每个节点的平衡因子只可能1、0、-1（即绝对值<=1，如果超过1，则称之为失衡）
  2. 每个节点的左右子树高度差不超过1
  3. 添加、搜索、删除的时间复杂度是O（logN）
     AVL树示例：
     

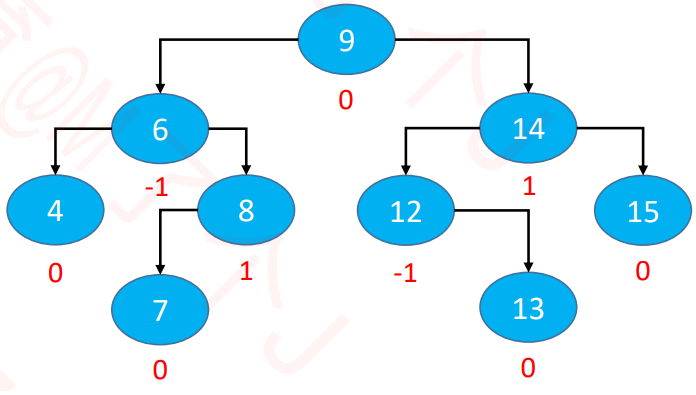
平衡对比

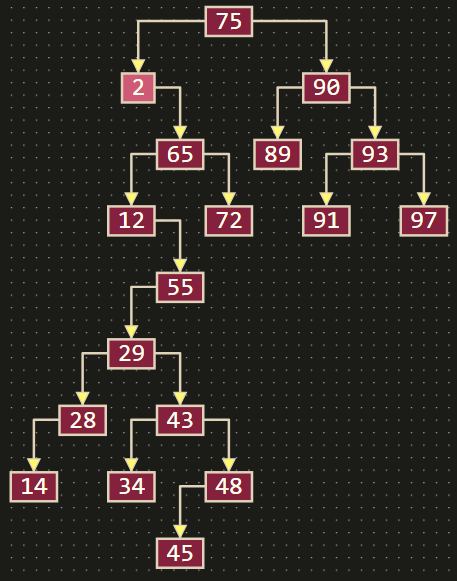
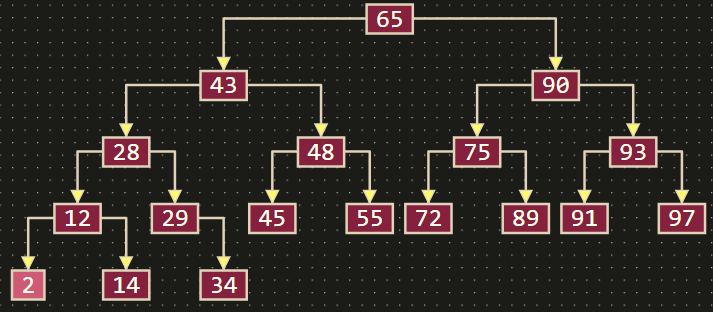
• 输入数据：75, 2, 90, 65, 12, 55, 93, 89, 29, 97, 43, 91, 48, 28, 72, 45, 14, 34
  普通二叉搜索树：
  
  AVL树：
  

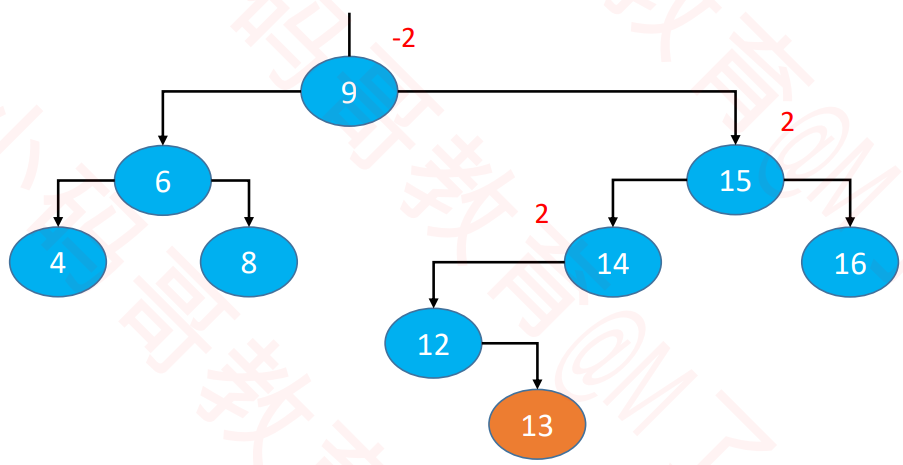
添加导致的失衡

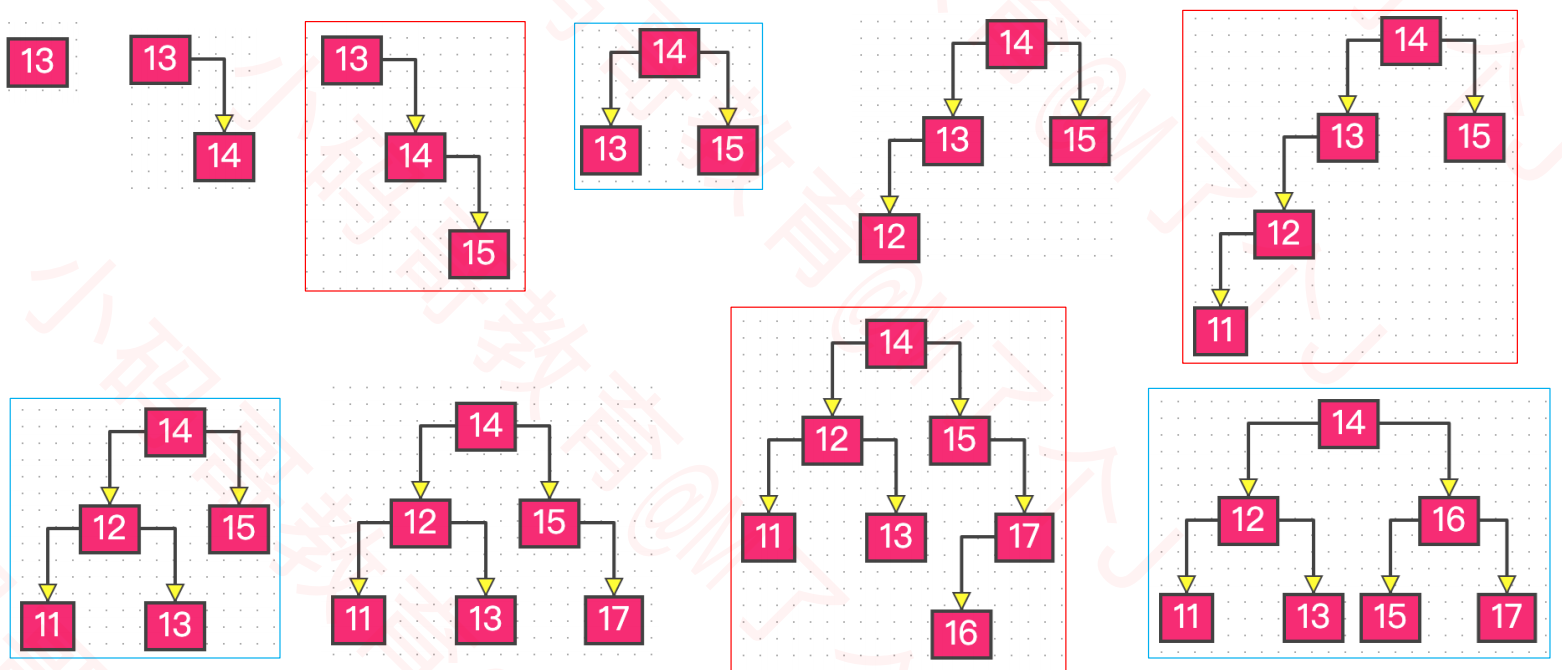
示例：往下面这颗子树中添加13

• 最坏情况：可能导致所有祖先节点都失衡
• 父节点、非祖先节点都不可能失衡
  

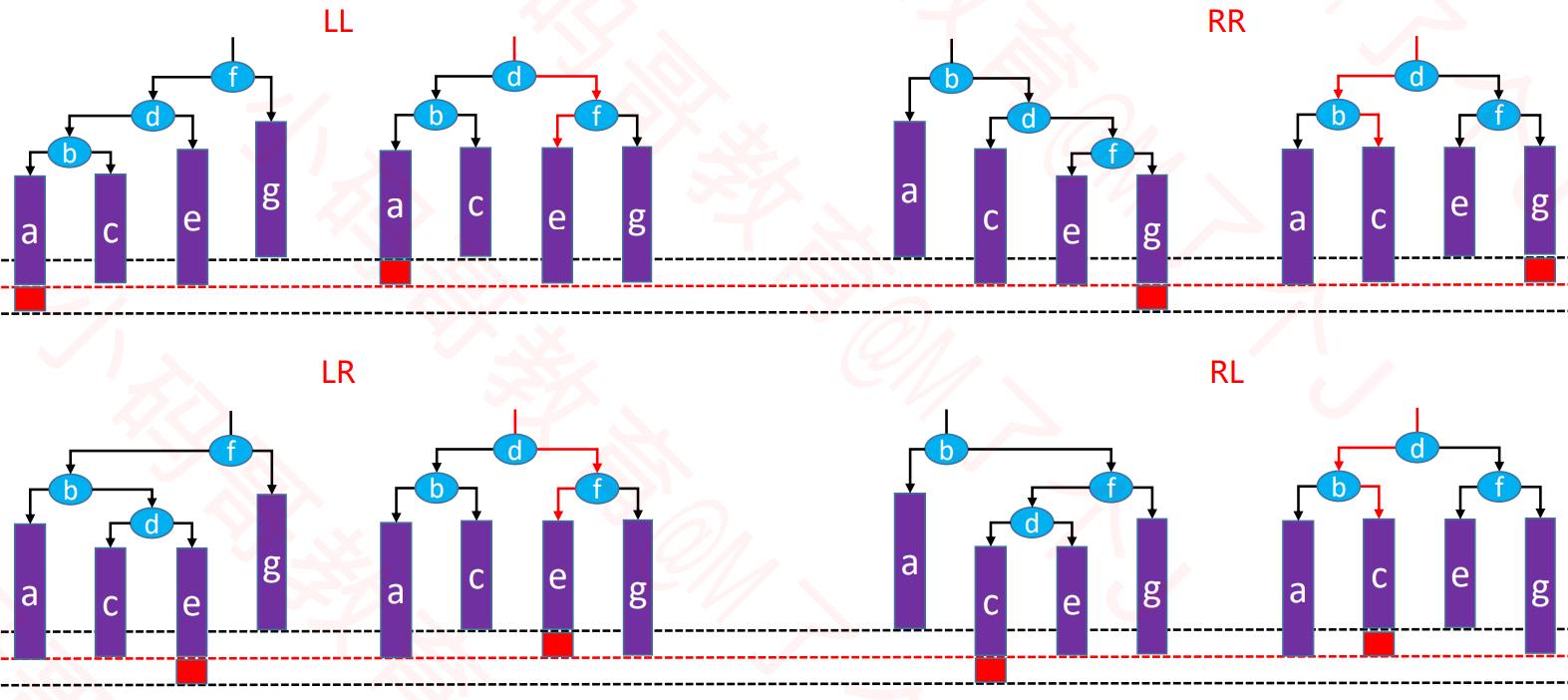
LL-右旋转（单旋）

//伪代码
g.left = p.right
p.right = g
让p成为这颗子树的根节点

• 仍然是一颗二叉搜索树：T0 < n < T1 < p < T2 < g < T3
  整棵树达到平衡
• 除此之外还需要维护的内容
  T2、p、g的parent属性
  先后更新g、p的高度
  

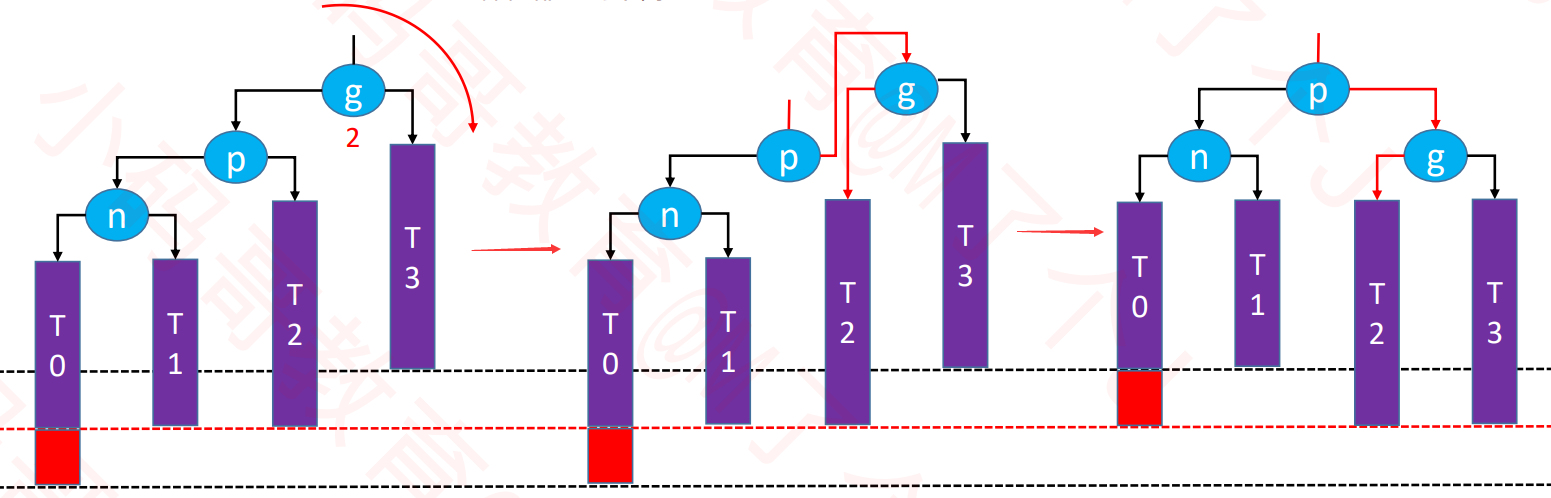
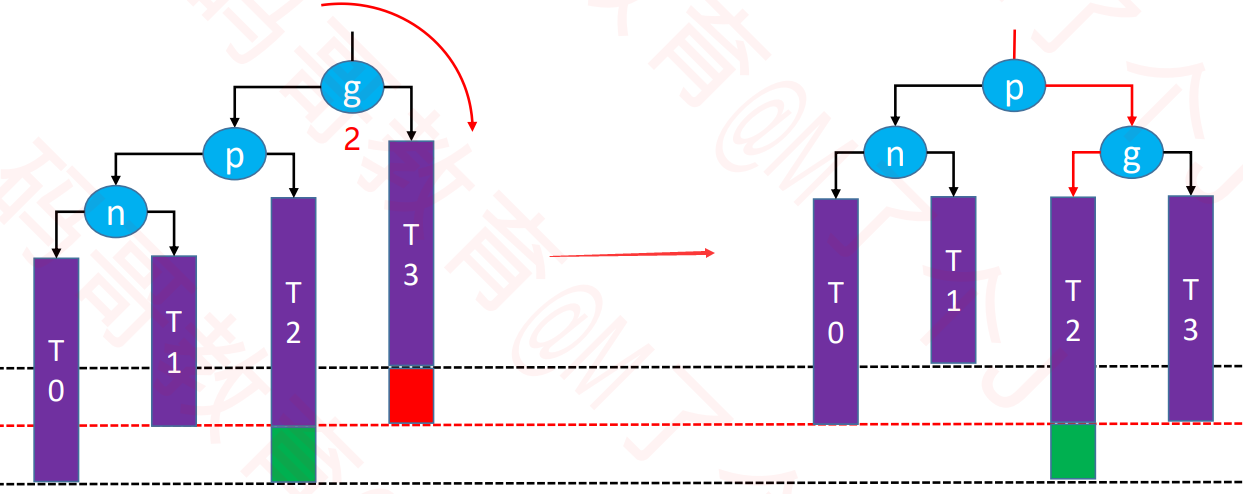
RR-左旋转（单旋）

//伪代码
g.right= p.left
p.left= g
让p成为这颗子树的根节点

• 仍然是一颗二叉搜索树：T0 < g < T1 < p < T2 < n < T3
  整棵树达到平衡
• 除此之外还需要维护的内容
  T1、p、g的parent属性
  先后更新g、p的高度
  

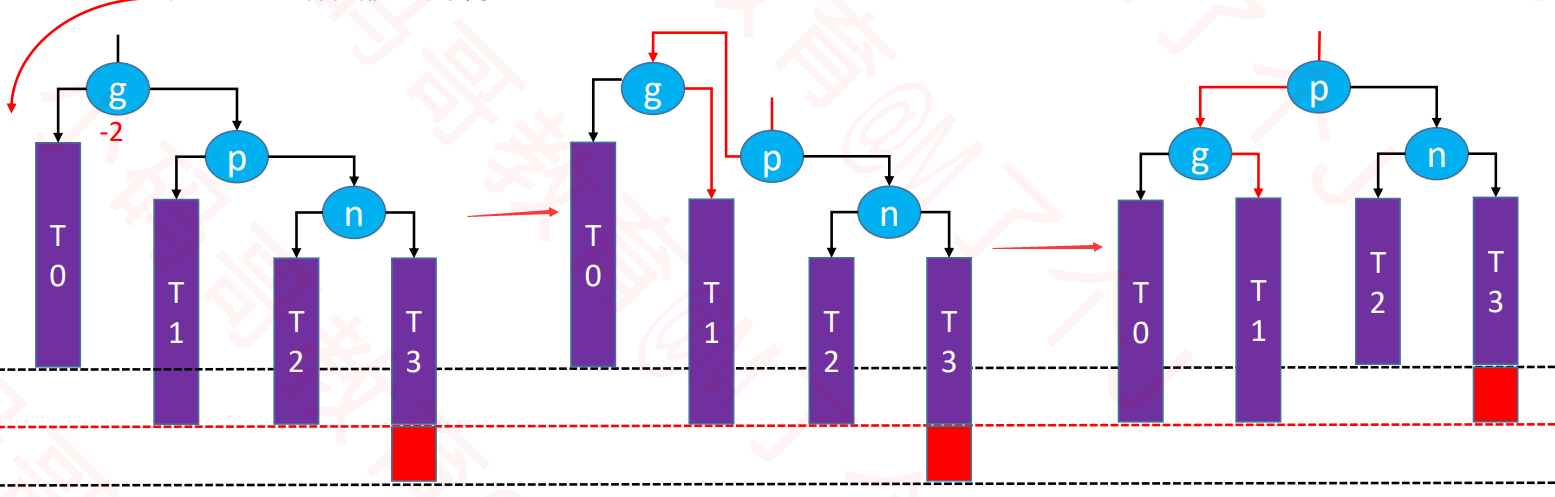
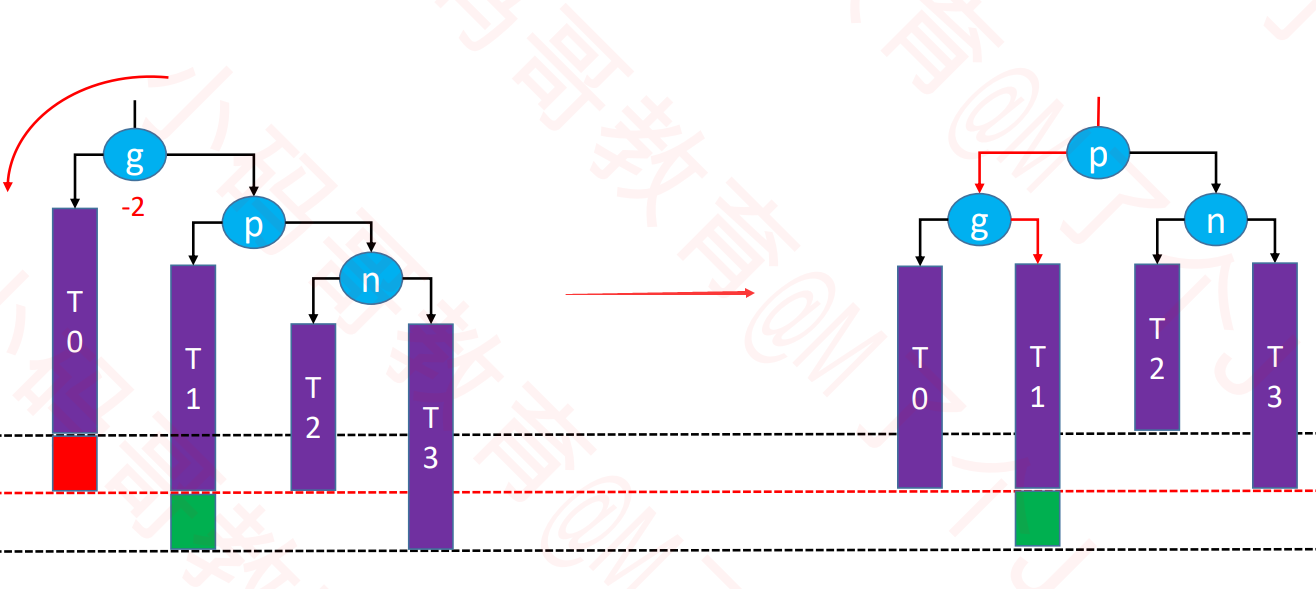
LR-RR左旋转，LL右旋转（双旋）

• 下图的p节点先左旋转，然后g节点再右旋转
  

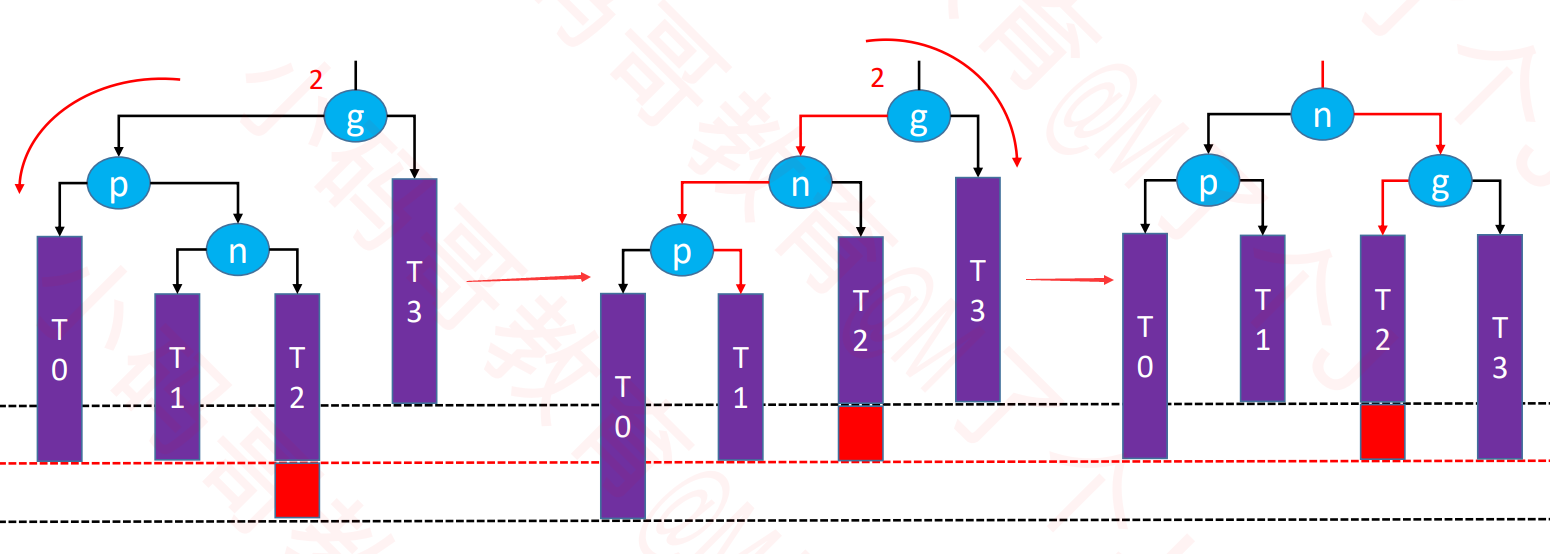
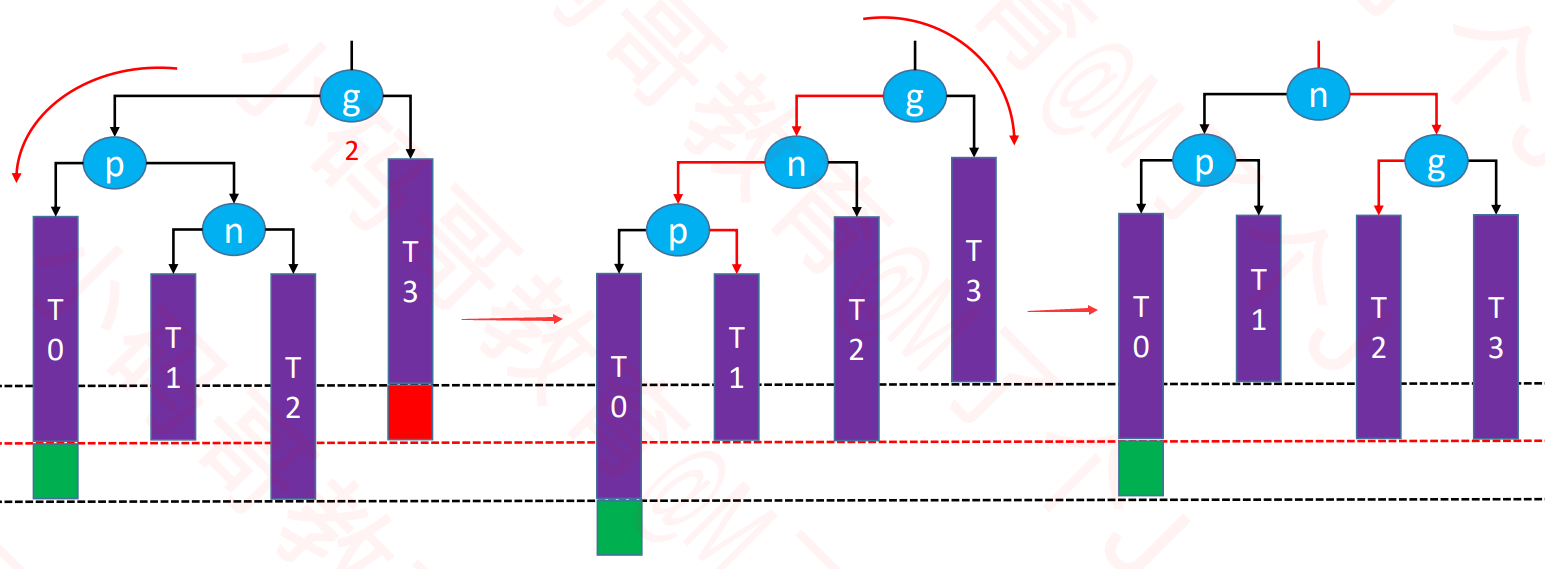
RL-LL右旋转，RR左旋转（双旋）

• 下图的p节点先右旋转，然后g节点再左旋转
  

添加之后的修复（代码）

//添加节点之后维持平衡
protected void afterAdd(Node<E> node) {
    while((node = node.parent) != null){
        //判断节点是否平衡
        if (isBalance(node)){
            //更新高度
            updateHeight(node);
        } else {
            //恢复平衡
            rebalance(node);
            //整棵树恢复平衡
            break;
        }
    }
}

/**
 * 恢复节点平衡
 * @param grand 高度最低的不平衡节点
 */
private void rebalance(Node<E> grand){
    Node<E> parent = ((AVLNode<E>)grand).tallerChild();
    Node<E> node = ((AVLNode<E>)parent).tallerChild();
    //判断父节点是否为祖父节点的左节点
    if (parent.isLeftChild()){ //L   父节点为祖父节点的左节点
        //判断子节点是否为父节点的左节点
        if(node.isLeftChild()){ //LL  子节点为父节点的左节点
            rotateRight(grand);
        } else { //LR  子节点为父节点的右节点
            rotateLeft(parent);
            rotateRight(grand);
        }
    } else { //R   父节点为祖父节点的右节点
        //判断子节点是否为父节点的左节点
        if(node.isLeftChild()){ //RL  子节点为父节点的左节点
            rotateRight(parent);
            rotateLeft(grand);
        } else { // RR   子节点为父节点的右节点
            rotateLeft(grand);
        }
    }
}

节点旋转（代码）

//左旋转
private void rotateLeft(Node<E> grand){
    //获取grand的右节点
    Node<E> parent = grand.right;
    //获取parent的左节点
    Node<E> child = parent.left;
    //左旋转动作
    grand.right = child;
    parent.left = grand;
    //维护parent和height
    afterRotate(grand,parent,child);
}

//右旋转
private void rotateRight(Node<E> grand){
    //获取grand的左节点
    Node<E> parent = grand.left;
    //获取parent的右节点
    Node<E> child = parent.right;
    //右旋转动作
    grand.left = child;
    parent.right = grand;
    //维护parent和height
    afterRotate(grand,parent,child);
}

/**
 * 旋转之后的执行代码
 * @param grand 失衡节点
 * @param parent 失衡节点的tallerChild
 * @param child g和g需要交换的子树（本来是parent的子树，后面会变成grand的子树）
 */
private void afterRotate(Node<E> grand, Node<E> parent, Node<E> child){
    //维护每个节点的父子节点关系
    //让parent节点成为子树的根节点
    parent.parent = grand.parent;
    if (grand.isLeftChild()){
        grand.parent.left = parent;
    } else if (grand.isRightChild()) {
        grand.parent.right = parent;
    } else {
        root = parent;
    }

    //更新child节点的parent
    if (child != null) child.parent = grand;

    //更新grand的parent节点
    grand.parent = parent;

    //更新高度
    updateHeight(grand);
    updateHeight(parent);
}

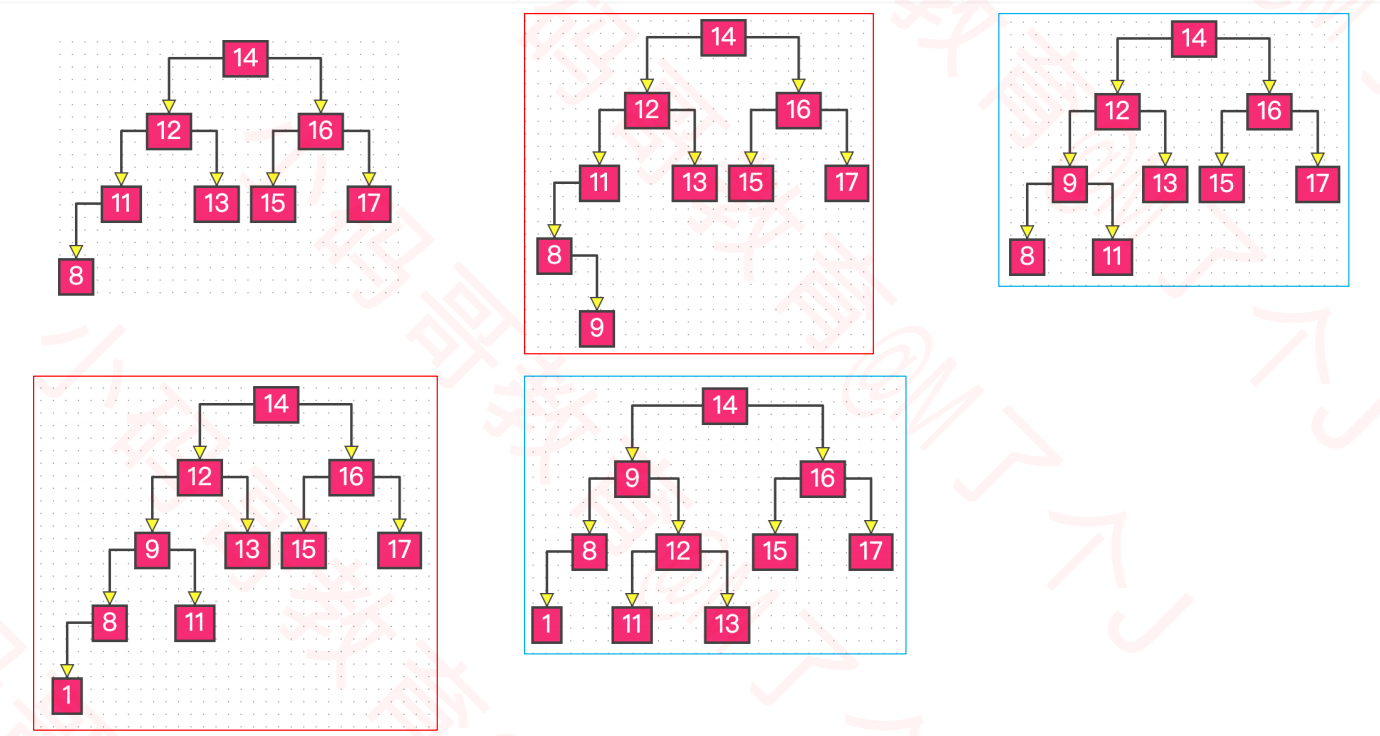
• 示例：输入数据：13，14，15，12，11，17，16，8，9，1
  

统一旋转操作

• 代码：

//统一旋转操作
private void rotate(
        Node<E> r,//根节点
        Node<E> a, Node<E> b, Node<E> c,
        Node<E> d,
        Node<E> e, Node<E> f, Node<E> g){
    //让d成为这颗子树的根节点
    d.parent = r.parent;
    if (r.isLeftChild()){
        r.parent.left = d;
    } else if (r.isRightChild()){
        r.parent.right = d;
    } else {
        root = d;
    }

    //a-b-c
    b.left = a;
    if (a != null) a.parent = b;
    b.right = c;
    if (c != null) c.parent = b;
    updateHeight(b);

    //e-f-g
    f.left = e;
    if (e != null) e.parent = f;
    f.right = g;
    if (g != null) g.parent = f;
    updateHeight(f);

    //b-d-f
    d.left = b;
    d.right = f;
    b.parent = d;
    f.parent = d;
    updateHeight(d);
}

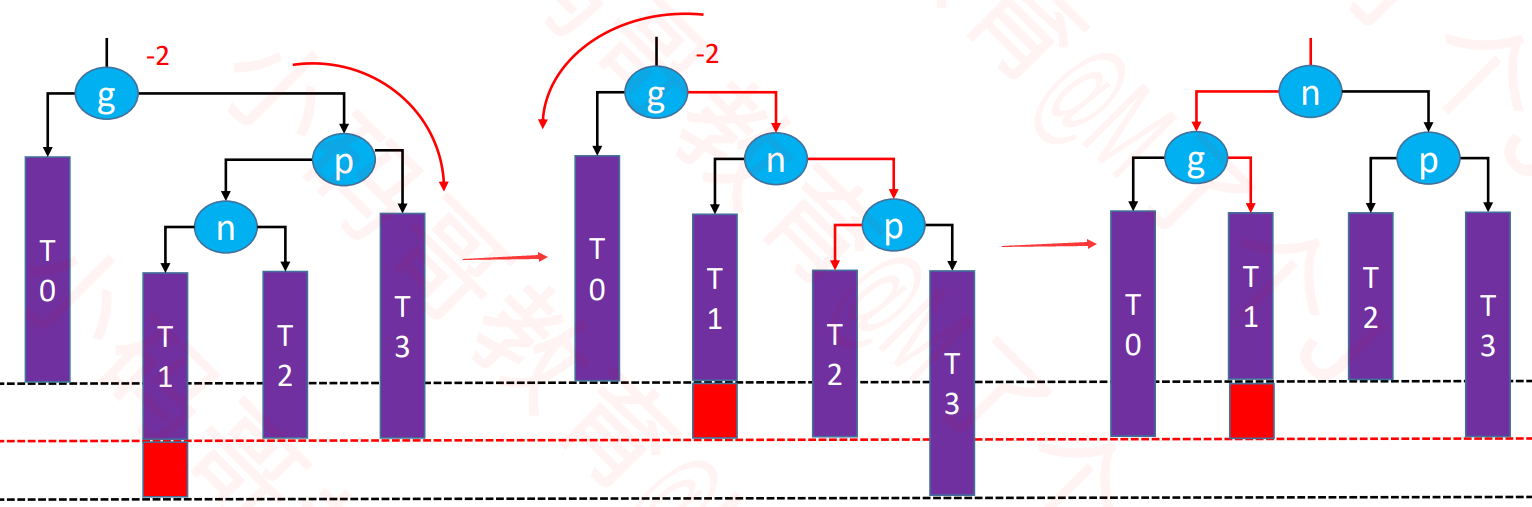
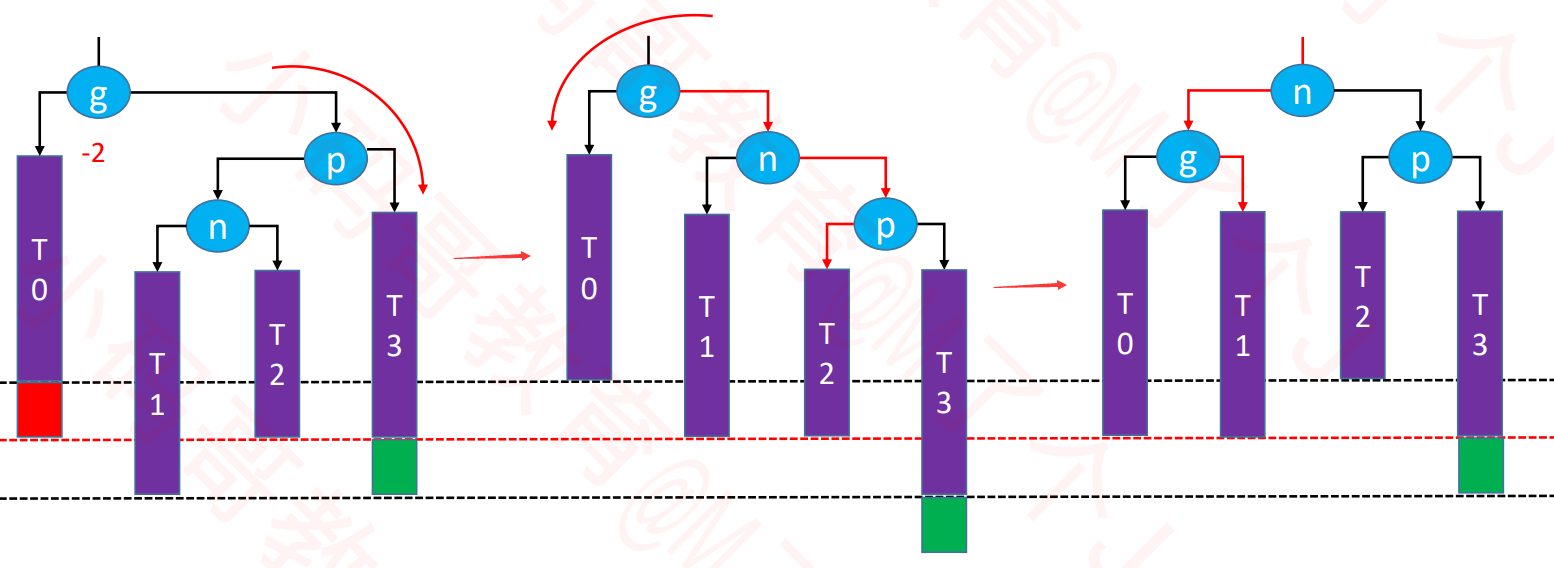
删除导致的失衡

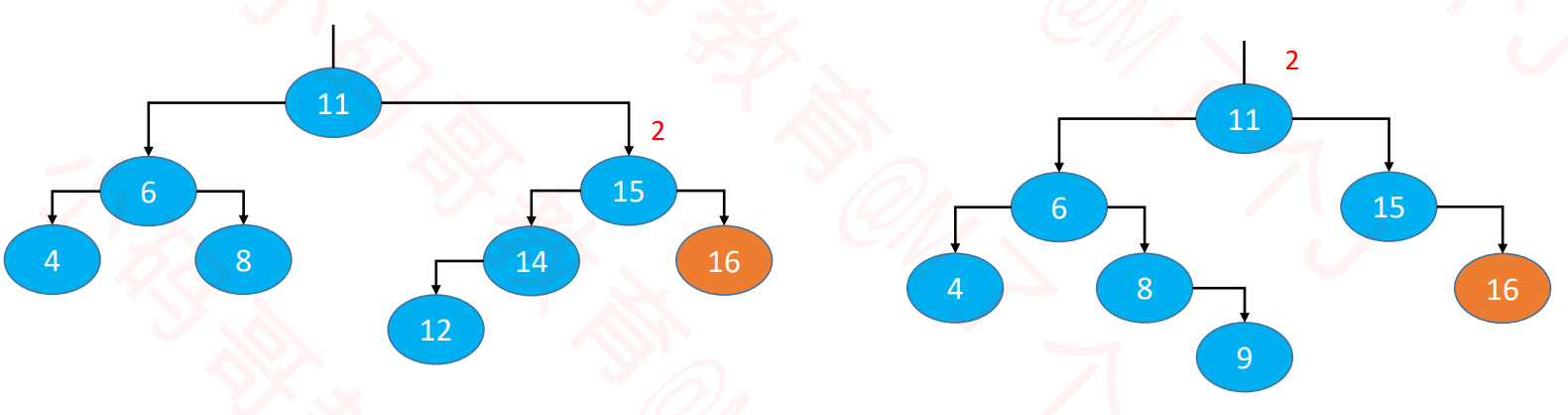
• 示例：删除下图两个子树中的16
• 可能会导致父节点或祖先节点失衡（只有一个节点会失衡），其他节点，都不可能失衡
  

LL-右旋转（单旋）

• 如果下图中绿色节点不存在，更高层的祖先节点也可能会失衡，需要再次恢复平衡，然后又可能导致更高层的祖先节点失衡。。。
• 极端情况下，所有祖先节点都需要进行恢复平衡的操作，共O（logN）次调整
  

RR-左旋转（单旋）

LR-RR左旋转，LL右旋转（双旋）

RL-LL右旋转，RR左旋转（双旋）

删除之后的修复（代码）

//删除节点之后维持平衡
protected void afterRemove(Node<E> node) {
    while((node = node.parent) != null){
        //判断节点是否平衡
        if (isBalance(node)){
            //更新高度
            updateHeight(node);
        } else {
            //恢复平衡
            rebalance(node);
            //整棵树恢复平衡
            break;
        }
    }
}

总结

1. 添加
   • 可能会导致所有祖先节点都失衡
   • 只要让高度最低的失衡节点恢复平衡，整棵树就恢复平衡（只需要O（1）次调整）
2. 删除
   • 可能会导致父节点或祖先节点失衡（只会导致一个节点失衡）
   • 恢复平衡后，可能会导致更高层的祖先节点失衡（最多需要O（logN）次调整）
3. 平均时间复杂度
   • 搜索：O（logN）
   • 添加：O（logN），仅需O（1）次的旋转操作
   • 删除：O（logN），最多需要O（logN）次的旋转操作