算法分析与实践-作业1

 最小生成树

1. 问题

        在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即）且为无循环图，使得的 w(T) 最小，则此 T 为 G 的最小生成树。

      

 

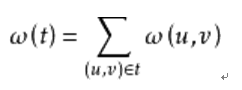
2. 解析

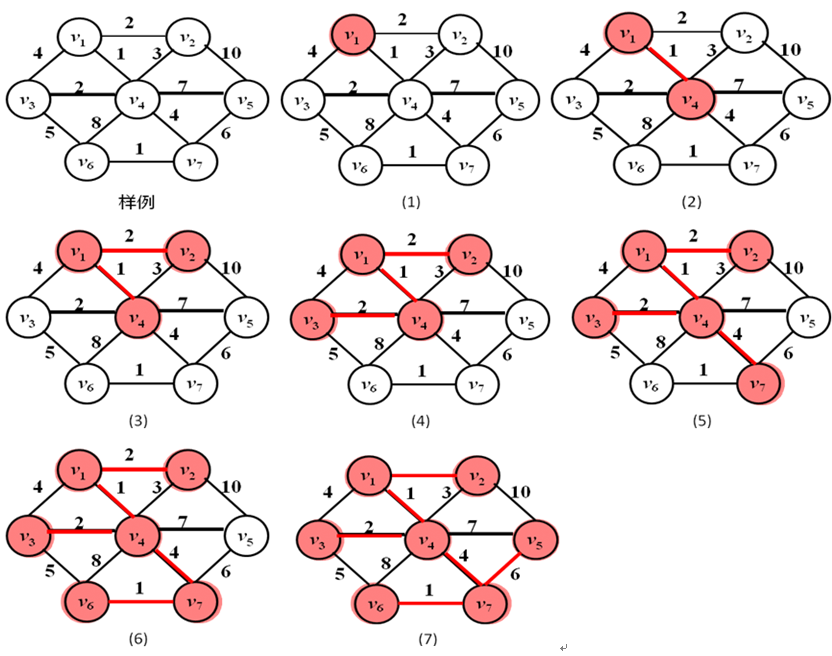
1.Prim算法：

        1).初始化：Vnew= {x}，其中x为集合V中的任一节点（起始点），Enew= {},为空；

        2).重复下列操作，直到Vnew= V：

                a.在集合E中选取权值最小的边<u, v>，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

                b.将v加入集合Vnew中，将<u, v>边加入集合Enew中；

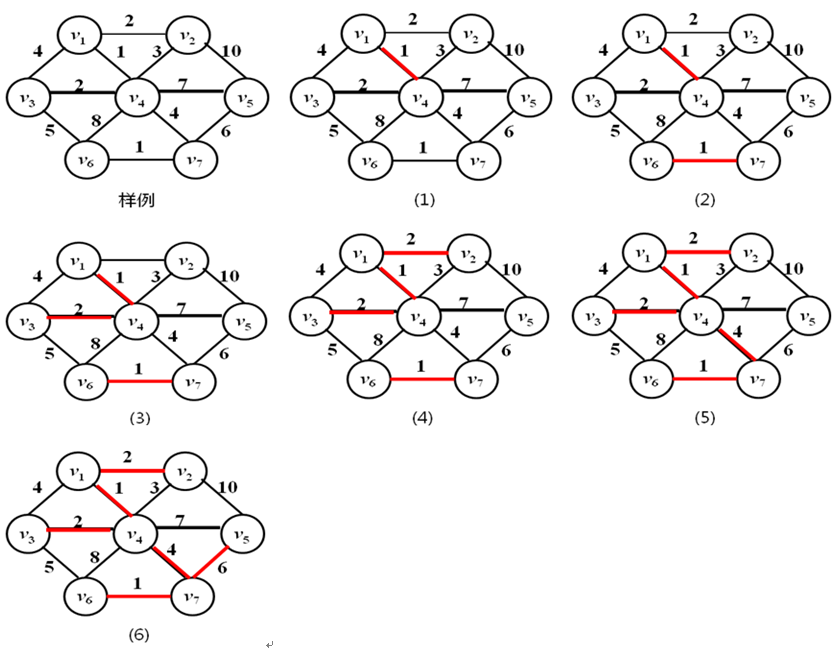
2.kruscal算法：

       先构造一个只含 n 个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有 n 棵树的一个森林。之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。

3. 设计

使用优先队列优化的prim算法：

#include<bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
const int maxm=100000+10;
int n,m;
int vis[maxn];        //用来判断该点是否在最小生成树中 
struct node{          //存边的信息 
    int to,dis;
    bool operator <(const node &a)const{
        return dis>a.dis;
    }
};
vector<node>e[maxn];             //用vector容器来存边 
priority_queue<node>q;           //优先队列优先选择边权最小的边 
/*----------以下为prim算法----------*/ 
void prim(){
    int ans=0;                   //表明最小生成树的权值 
    int cnt=0;                   //表明在最小生成树中的点的数量 
    q.push((node){1,0});
    while(!q.empty()&&cnt<n){
        node k=q.top();q.pop();
        if(vis[k.to])continue;   //表明该点已经在最小生成树中 
        vis[k.to]=1;
        ans+=k.dis;
        cnt++;
        for(int i=0;i<e[k.to].size();++i){
            if(!vis[e[k.to][i].to]){
                q.push((node){e[k.to][i].to,e[k.to][i].dis});
            }
        }
    }
    printf("%d
",cnt==n?ans:-1);
}
/*----------以上为prim算法----------*/ 
void init(){                    //初始化 
    while(!q.empty())q.pop();
    for(int i=1;i<=n;++i)e[i].clear(),vis[i]=0;
}
int main(){
    while(scanf("%d %d",&n,&m)!=EOF){    //n代表点的数量，m代表边的数量 
        init();
        for(int i=1;i<=m;++i){
            int x,y,z;
            scanf("%d %d %d",&x,&y,&z);
            e[x].push_back((node){y,z});
            e[y].push_back((node){x,z});
        }
        prim();
    }
    return 0;
}

kruscal算法：

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=100000+10;
const int maxm=100000+10;
int n,m;
struct edge{
    int from,to,cost;
}e[maxm];
bool cmp(struct edge &a,struct edge &b){
    return a.cost<b.cost;
}
/*----------以下为通过并查集维护联通快----------*/
int fa[maxn];
int find(int x){
    return fa[x]==x?fa[x]:fa[x]=find(fa[x]);
}
void baba(int x,int y){
    int fx=find(x),fy=find(y);
    fa[fx]=fy;
}
/*----------以上为通过并查集维护联通快----------*/
/*----------以下为kruskal----------*/
int kruskal(){
    int cnt=1;                     //表明包含在最小生成树内的点的数量 
    int res=0;                     //表明最小生成树的边权和 
    sort(e+1,e+1+m,cmp);           //将每条边按照权值从小到大进行排序 
    for(int i=1;i<=m;++i){
        int fx=find(e[i].from),fy=find(e[i].to);
        if(fx==fy)continue;        //若在同一联通块内，则调过本次循环 
        baba(e[i].from,e[i].to);   //联通e[i].from和e[i].to 
        cnt++;
        res+=e[i].cost;
        if(cnt==n)break;
    }
    return cnt==n?res:-1;   //若cnt不等于n,则表明无法生成最小生成树,输出-1 
}
/*----------以上为kruskal----------*/
void init(){  //初始化 
    for(int i=1;i<=n;++i)fa[i]=i;
}
int main(){
    while(scanf("%d %d",&n,&m)!=EOF){   //n表示点的数量,m表示边的数量 
        init();
        for(int i=1;i<=m;++i){
            scanf("%d %d %d",&e[i].from,&e[i].to,&e[i].cost);
        }
        printf("%d
",kruskal());
    }
}

4. 分析

//n为点的数量，m为边的数量

使用优先队列的Prim复杂度为：mlogn

Kruscal算符复杂度为：mlogm

5. 源码

Kruscal：https://github.com/JayShao-Xie/algorithm-work/blob/master/kruskal.cpp

Prim：https://github.com/JayShao-Xie/algorithm-work/blob/master/prim.cpp