LCS算法

3. 设计
1 #include<stdio.h> 2 #include<string.h> 3 const int maxn = 1000 + 10; 4 char x[maxn], y[maxn]; 5 int dp[maxn][maxn]; 6 int b[maxn][maxn]; //b[i][j]=0为删除两个,b[i][j]=1为删除x,b[i][j]=2为删除y 7 char lcs[maxn]; 8 int n, m; //n为字符串x的长度,m为字符串y的长度 9 int main() { 10 scanf("%d", &n); 11 scanf("%s", x + 1); 12 scanf("%d", &m); 13 scanf("%s", y + 1); 14 //初始化 15 for (int i = 0; i <= m; ++i)dp[0][i] = 0; 16 for (int i = 0; i <= n; ++i)dp[i][0] = 0; 17 18 /*----------以下为求最长公共子序列长度----------*/ 19 for (int i = 1; i <= n; ++i) { 20 for (int j = 1; j <= m; ++j) { 21 if (x[i] == y[j]) { 22 dp[i][j] = dp[i - 1][j - 1] + 1; 23 } 24 else { 25 if (dp[i - 1][j] > dp[i][j - 1]) { 26 b[i][j] = 1; 27 dp[i][j] = dp[i - 1][j]; 28 } 29 else { 30 b[i][j] = 2; 31 dp[i][j] = dp[i][j - 1]; 32 } 33 } 34 } 35 } 36 /*----------以上为求最长公共子序列长度----------*/ 37 /*----------以下为求最长公共子序列----------*/ 38 int i = n, j = m; 39 while (i != 0 && j != 0) { 40 if (b[i][j] == 0) { 41 lcs[dp[i][j]] = x[i]; 42 i--, j--; 43 } 44 else if (b[i][j] == 1) { 45 i--; 46 } 47 else { 48 j--; 49 } 50 } 51 /*----------以上为求最长公共子序列----------*/ 52 printf("最长公共子序列长度为:%d ", dp[n][m]); 53 if (dp[n][m] != 0) { 54 printf("最长公共子序列为:"); 55 for (int i = 1; i <= dp[n][m]; ++i) { 56 printf("%c", lcs[i]); 57 } 58 } 59 }
4. 分析
T(n)=O(nm)
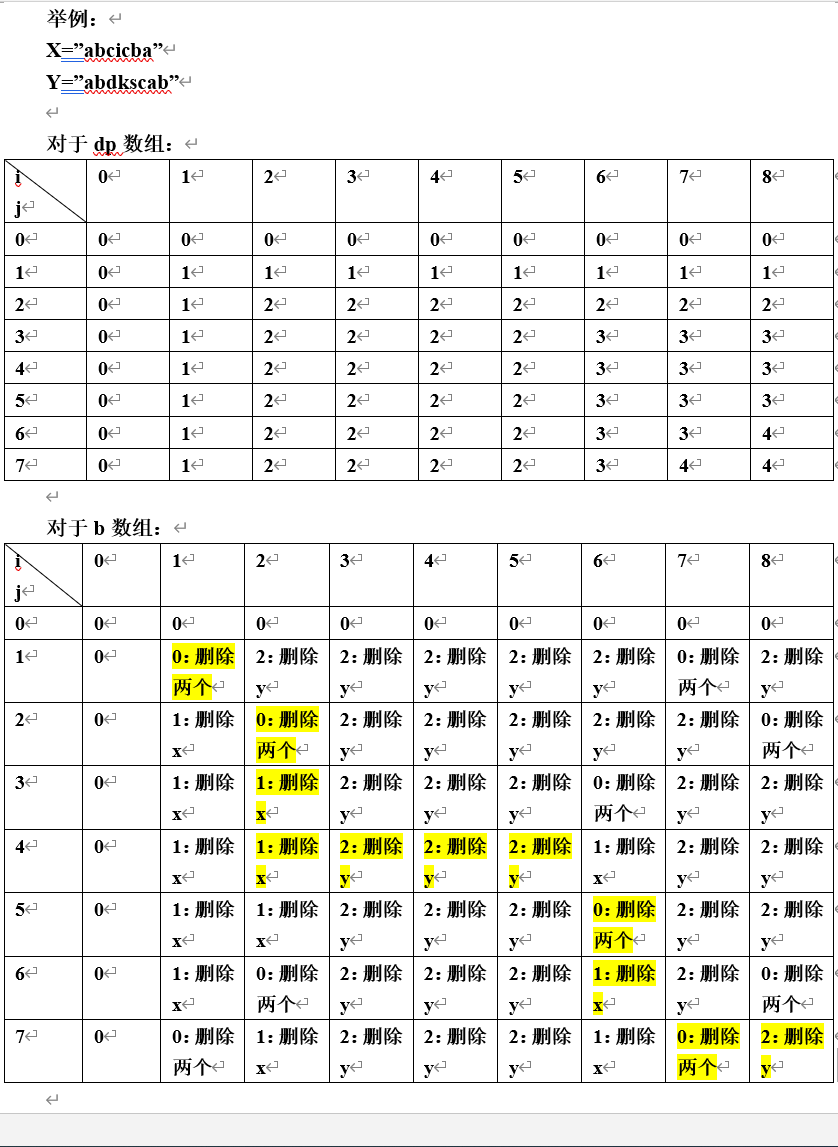

5. 源码
https://github.com/JayShao-Xie/algorithm-work/blob/master/LCS.cpp