C#编程总结（七）数据加密——附源码

C#编程总结（七）数据加密——附源码

Posted on 2014-01-26 16:39 停留的风 阅读(16874) 评论(15) 编辑 收藏

C#编程总结（七）数据加密——附源码

 概述

数据加密的基本过程就是对原来为明文的文件或数据按某种算法进行处理，使其成为不可读的一段代码，通常称为“密文”，使其只能在输入相应的密钥之后才能显示出本来内容，通过这样的途径来达到保护数据不被非法人窃取、阅读的目的。 该过程的逆过程为解密，即将该编码信息转化为其原来数据的过程。加密建立在对信息进行数学编码和解码的基础上。加密类型分为两种，对称加密与非对称加密，对称加密双方采用共同密钥。非对称加密，这种加密方式存在两个密钥，一个是公共密钥（对外公开），一种是私人密钥（对外保密）。  

一、摘要算法

数据摘要算法是密码学算法中非常重要的一个分支，它通过对所有数据提取指纹信息以实现数据签名、数据完整性校验等功能，由于其不可逆性，有时候会被用做敏感信息的加密。数据摘要算法也被称为哈希（Hash）算法或散列算法。

从严格意义上讲，摘要算法不是加密算法，但在具体应用中类似于加密算法使用，或者与加密算法一起使用，这里也拿来介绍下。

应用范围：密码加密、数据完整性校验、数字签名等

这里介绍常用的两种摘要算法，MD5与SHA1。

提示：当前MD5已经被破解，推荐使用SHA1

1、MD5

哈希函数将任意长度的二进制字符串映射为固定长度的小型二进制字符串。 加密哈希函数有这样一个属性：在计算上不大可能找到散列为相同的值的两个不同的输入；也就是说，两组数据的哈希值仅在对应的数据也匹配时才会匹配。 数据的少量更改会在哈希值中产生不可预知的大量更改。MD5 算法的哈希值大小为 128 位。
MD5 类的 ComputeHash 方法将哈希作为 16 字节的数组返回。 请注意，某些 MD5 实现会生成 32 字符的十六进制格式哈希。 若要与此类实现进行互操作，请将 ComputeHash 方法的返回值格式化为十六进制值。

 MD5加密：

        /// <summary>
        /// MD5加密为32字符长度的16进制字符串
        /// </summary>
        /// <param name="input"></param>
        /// <returns></returns>
        public static string EncryptByMD5(string input)
        {
            MD5 md5Hasher = MD5.Create();
            byte[] data = md5Hasher.ComputeHash(Encoding.UTF8.GetBytes(input));

            StringBuilder sBuilder = new StringBuilder();
            //将每个字节转为16进制
            for (int i = 0; i < data.Length; i++)
            {
                sBuilder.Append(data[i].ToString("x2"));
            }

            return sBuilder.ToString();            
        }

  

2、SHA1

计算输入数据的 SHA1 哈希值。

哈希值用作表示大量数据的固定大小的唯一值。 如果相应的数据也匹配，则两个数据集的哈希应该匹配。 数据的少量更改会在哈希值中产生不可预知的大量更改。
SHA1 算法的哈希值大小为 160 位。

 SHA1加密：

        /// <summary>
        /// SHA1加密
        /// </summary>
        /// <param name="input"></param>
        /// <returns></returns>
        public static string EncryptBySHA1(string input)
        {
            SHA1 sha = new SHA1CryptoServiceProvider();          
            byte[] bytes = Encoding.Unicode.GetBytes(input);
            byte[] result = sha.ComputeHash(bytes);
            return BitConverter.ToString(result);
        }

  

 二、对称加密

对称加密(也叫私钥加密)指加密和解密使用相同密钥的加密算法。有时又叫传统密码算法，就是加密密钥能够从解密密钥中推算出来，同时解密密钥也可以从加密密钥中推算出来。而在大多数的对称算法中，加密密钥和解密密钥是相同的，所以也称这种加密算法为秘密密钥算法或单密钥算法。

原理图：

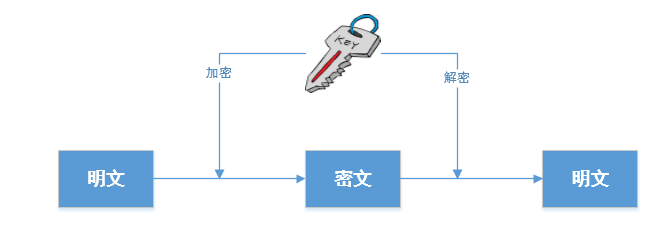
优点：算法公开、计算量小、加密速度快、加密效率高。
缺点：密钥管理困难，使用成本较高。与公开密钥加密算法比起来，对称加密算法能够提供加密和认证却缺乏了签名功能，使得使用范围有所缩小。

常用的对称加密算法有：DES、IDEA、RC2、RC4、SKIPJACK、RC5、AES算法等

应用场景：数据传输、大数据量加密、敏感数据加密等等

这里重点介绍常用的DES与AES加密算法。

提示: DES已经被破解，推荐使用3DES或AES

1、DES 

最早、最著名的保密密钥或对称密钥加密算法DES(Data Encryption Standard)是由IBM公司在70年代发展起来的，并经政府的加密标准筛选后，于1976年11月被美国政府采用，DES随后被美国国家标准局和美国国家标准协会（American National Standard Institute，ANSI）承认。
DES使用56位密钥对64位的数据块进行加密，并对64位的数据块进行16轮编码。与每轮编码时，一个48位的"每轮"密钥值由56位的完整密钥得出来。DES用软件进行解码需用很长时间，而用硬件解码速度非常快。幸运的是，当时大多数黑客并没有足够的设备制造出这种硬件设备。在1977年，人们估计要耗资两千万美元才能建成一个专门计算机用于DES的解密，而且需要12个小时的破解才能得到结果。当时DES被认为是一种十分强大的加密方法。
随着计算机硬件的速度越来越快，制造一台这样特殊的机器的花费已经降到了十万美元左右，而用它来保护十亿美元的银行，那显然是不够保险了。另一方面，如果只用它来保护一台普通服务器，那么DES确实是一种好的办法，因为黑客绝不会仅仅为入侵一个服务器而花那么多的钱破解DES密文。

但是，这个算法，现在已经能够轻易破解。不过对于日常的非机密文件同样可以继续使用。

 加密：

        /// <summary>
        /// 加密字符串
        /// </summary>
        /// <param name="input"></param>
        /// <param name="sKey"></param>
        /// <returns></returns>
        public static string EncryptString(string input, string sKey)
        {
            byte[] data = Encoding.UTF8.GetBytes(input);
            using (DESCryptoServiceProvider des = new DESCryptoServiceProvider())
            {
                des.Key = ASCIIEncoding.ASCII.GetBytes(sKey);
                des.IV = ASCIIEncoding.ASCII.GetBytes(sKey);
                ICryptoTransform desencrypt = des.CreateEncryptor();
                byte[] result = desencrypt.TransformFinalBlock(data, 0, data.Length);
                return BitConverter.ToString(result);
            }            
        }

解密：

        /// <summary>
        /// 解密字符串
        /// </summary>
        /// <param name="input"></param>
        /// <param name="sKey"></param>
        /// <returns></returns>
        public static string DecryptString(string input, string sKey)
        {
            string[] sInput = input.Split("-".ToCharArray());
            byte[] data = new byte[sInput.Length];
            for (int i = 0; i < sInput.Length; i++)
            {
                data[i] = byte.Parse(sInput[i], NumberStyles.HexNumber);
            }
            using (DESCryptoServiceProvider des = new DESCryptoServiceProvider())
            {
                des.Key = ASCIIEncoding.ASCII.GetBytes(sKey);
                des.IV = ASCIIEncoding.ASCII.GetBytes(sKey);
                ICryptoTransform desencrypt = des.CreateDecryptor();
                byte[] result = desencrypt.TransformFinalBlock(data, 0, data.Length);
                return Encoding.UTF8.GetString(result);
            }
        }

  

2、AES

表示高级加密标准 (AES) 的所有实现都必须从中继承的抽象基类。

密码学中的高级加密标准（Advanced Encryption Standard，AES），又称Rijndael加密法，是美国联邦政府采用的一种区块加密标准。这个标准用来替代原先的DES，已经被多方分析且广为全世界所使用。

加密：

        /// <summary>  
        /// AES加密算法  
        /// </summary>  
        /// <param name="input">明文字符串</param>  
        /// <param name="key">密钥</param>  
        /// <returns>字符串</returns>  
        public static string EncryptByAES(string input, string key)
        {
            byte[] keyBytes = Encoding.UTF8.GetBytes(key.Substring(0, 32));
            using (AesCryptoServiceProvider aesAlg = new AesCryptoServiceProvider())
            {
                aesAlg.Key = keyBytes;
                aesAlg.IV = AES_IV;

                ICryptoTransform encryptor = aesAlg.CreateEncryptor(aesAlg.Key, aesAlg.IV);
                using (MemoryStream msEncrypt = new MemoryStream())
                {
                    using (CryptoStream csEncrypt = new CryptoStream(msEncrypt, encryptor, CryptoStreamMode.Write))
                    {
                        using (StreamWriter swEncrypt = new StreamWriter(csEncrypt))
                        {
                            swEncrypt.Write(input);
                        }
                        byte[] bytes = msEncrypt.ToArray();
                        //return Convert.ToBase64String(bytes);//此方法不可用
                        return BitConverter.ToString(bytes);
                    }
                }
            }
        }

解密：

        /// <summary>  
        /// AES解密  
        /// </summary>  
        /// <param name="input">密文字节数组</param>  
        /// <param name="key">密钥</param>  
        /// <returns>返回解密后的字符串</returns>  
        public static string DecryptByAES(string input, string key)
        {
            //byte[] inputBytes = Convert.FromBase64String(input); //Encoding.UTF8.GetBytes(input);
            string[] sInput = input.Split("-".ToCharArray());
            byte[] inputBytes = new byte[sInput.Length];
            for (int i = 0; i < sInput.Length; i++)
            {
                inputBytes[i] = byte.Parse(sInput[i], NumberStyles.HexNumber);
            }
            byte[] keyBytes = Encoding.UTF8.GetBytes(key.Substring(0, 32)); 
            using (AesCryptoServiceProvider aesAlg = new AesCryptoServiceProvider())
            {
                aesAlg.Key = keyBytes;
                aesAlg.IV = AES_IV;

                ICryptoTransform decryptor = aesAlg.CreateDecryptor(aesAlg.Key, aesAlg.IV);
                using (MemoryStream msEncrypt = new MemoryStream(inputBytes))
                {
                    using (CryptoStream csEncrypt = new CryptoStream(msEncrypt, decryptor, CryptoStreamMode.Read))
                    {
                        using (StreamReader srEncrypt = new StreamReader(csEncrypt))
                        {
                            return srEncrypt.ReadToEnd();
                        }
                    }
                }
            }           
        }

三、非对称加密算法 

概念：

非对称加密算法需要两个密钥：公开密钥（publickey）和私有密钥（privatekey）。公开密钥与私有密钥是一对，如果用公开密钥对数据进行加密，只有用对应的私有密钥才能解密；如果用私有密钥对数据进行加密，那么只有用对应的公开密钥才能解密。因为加密和解密使用的是两个不同的密钥，所以这种算法叫作非对称加密算法。 非对称加密算法实现机密信息交换的基本过程是：甲方生成一对密钥并将其中的一把作为公用密钥向其它方公开；得到该公用密钥的乙方使用该密钥对机密信息进行加密后再发送给甲方；甲方再用自己保存的另一把专用密钥对加密后的信息进行解密。另一方面，甲方可以使用乙方的公钥对机密信息进行签名后再发送给乙方；乙方再用自己的私匙对数据进行验签。甲方只能用其专用密钥解密由其公用密钥加密后的任何信息。 非对称加密算法的保密性比较好，它消除了最终用户交换密钥的需要。

原理图：

场景1：发送者用接收者的公钥加密，接受者用自己的私钥解密，具体如下图

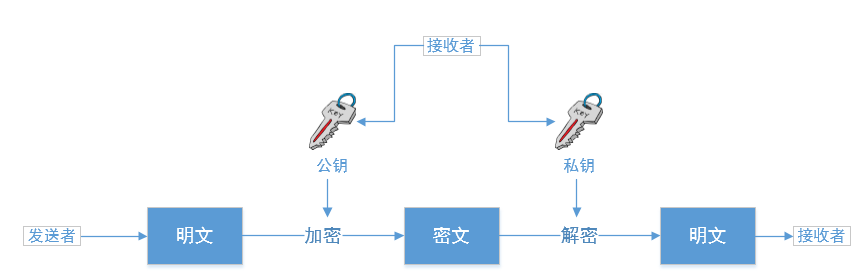
场景2：发送者用自己的私钥加密，接收者用发送者公布的公钥解密，具体如下图

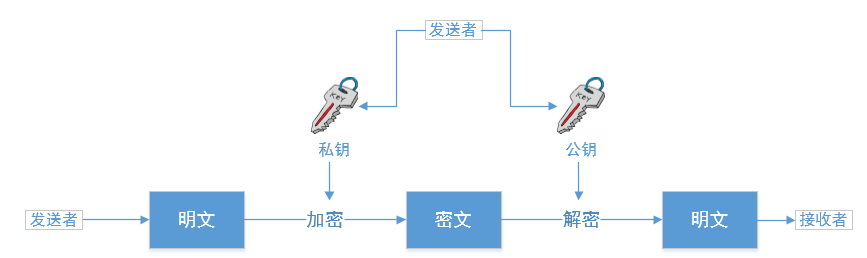
场景3：数字签名中应用，这里暂不进行介绍，后续有相关文章进行详细介绍。

见：http://www.cnblogs.com/yank/p/3533998.html

优点：非对称加密体系不要求通信双方事先传递密钥或有任何约定就能完成保密通信，并且密钥管理方便，可实现防止假冒和抵赖，因此，更适合网络通信中的保密通信要求

主要算法：RSA、Elgamal、背包算法、Rabin、D-H、ECC（椭圆曲线加密算法）。

1、RSA

RSA(Rivest-Shamir-Adleman)算法是基于大数不可能被质因数分解假设的公钥体系。简单地说就是找两个很大的质数。一个对外公开的为"公钥"（Public key） ，另一个不告诉任何人，称为"私钥"（Private key）。这两个密钥是互补的，也就是说用公钥加密的密文可以用私钥解密，反过来也一样。

假设用户甲要寄信给用户乙，他们互相知道对方的公钥。甲就用乙的公钥加密邮件寄出，乙收到后就可以用自己的私钥解密出甲的原文。由于别人不知道乙的私钥，所以即使是甲本人也无法解密那封信，这就解决了信件保密的问题。另一方面，由于每个人都知道乙的公钥，他们都可以给乙发信，那么乙怎么确信是不是甲的来信呢？那就要用到基于加密技术的数字签名了。
甲用自己的私钥将签名内容加密，附加在邮件后，再用乙的公钥将整个邮件加密（注意这里的次序，如果先加密再签名的话，别人可以将签名去掉后签上自己的签名，从而篡改了签名）。这样这份密文被乙收到以后，乙用自己的私钥将邮件解密，得到甲的原文和数字签名，然后用甲的公钥解密签名，这样一来就可以确保两方面的安全了。

加密：

        /// <summary>
        /// RSA加密
        /// </summary>
        /// <param name="plaintext">明文</param>
        /// <param name="publicKey">公钥</param>
        /// <returns>密文字符串</returns>
        public static string EncryptByRSA(string plaintext, string publicKey)
        {           
            UnicodeEncoding ByteConverter = new UnicodeEncoding();         
            byte[] dataToEncrypt = ByteConverter.GetBytes(plaintext);
            using (RSACryptoServiceProvider RSA = new RSACryptoServiceProvider())
            {
                RSA.FromXmlString(publicKey);
                byte[] encryptedData = RSA.Encrypt(dataToEncrypt, false);
                return Convert.ToBase64String(encryptedData);
            }
        }

解密：

        /// <summary>
        /// RSA解密
        /// </summary>
        /// <param name="ciphertext">密文</param>
        /// <param name="privateKey">私钥</param>
        /// <returns>明文字符串</returns>
        public static string DecryptByRSA(string ciphertext, string privateKey)
        {
            UnicodeEncoding byteConverter = new UnicodeEncoding();
            using (RSACryptoServiceProvider RSA = new RSACryptoServiceProvider())
            {
                RSA.FromXmlString(privateKey);
                byte[] encryptedData = Convert.FromBase64String(ciphertext);
                byte[] decryptedData = RSA.Decrypt(encryptedData, false);
                return byteConverter.GetString(decryptedData);
            }
        }

所有案例，见测试DEMO

源码地址：http://files.cnblogs.com/yank/EncriptSample.zip