本文为转载 下面的源码为AS3代码 原文地址
最近正好在做寻路算法,最近看了很多资料,本来想自己写一篇的总结一下的,但是看了这个以后,感觉这个已经写的很通俗易懂了,所以偷了个懒,直接转载了。
我最后用的不是A星,直接用的最短路径算法,代码只有50行左右,但是跟这个原理其实差不多,改天加了详细注释以后再把我自己的代码贴出来。
无上天君与梦瑶的传说
序章,仙界天山住着一位威震仙界的大神(无上天君),我们假设我们就是这位无上天君,我们有神识亿万分身术和卫星定位系统(谁说神仙不会高科技),这可是我们寻路的资本!
第一章,传说美丽的天外仙岛有一个仙女,她叫做梦瑶,她是所有程序神猿的终极梦想,但谁也不知道这座仙岛在什么地方,只知道在仙界之外。无上天君也一直喜欢着这位未知的仙女,以致于单身数万年。
第二章,我们(无上天君)偶然得到了一张太古的天外地图,这里面记载着去天外仙道的路,但由于太古文字过于古老,我们也无法知道路在何方,但至少我们有了地图。
第三章,我们是谁?我们是拥有卫星定位系统的无上天君,这样通过地图加上系统,我们锁定了仙岛的位置和自己的位置。我们通过系统的雷达辅助,就可以实时计算我们所处位置到仙道的大致距离。
第四章,一张地图、神识亿万分身术和卫星定位系统我们拥有这些,但路依然是未知的,那么重点来了,我们需要寻路!!!
第五章,我们发明了一种算法叫做 F 算法(F = G + H),这种算法可以帮助我们确定自己和仙岛的距离,F 是我们从天山到仙岛的估算距离,G 是我们从天山到现在所处位置的实际距离,H 是我们从现在位置到仙岛的估算距离。
第六章,天外一直是禁地,各种远古萌兽、死亡绝地等等不知吞噬了多少仙界大神的神格。但我们拥有神识亿万分身术,可以用分身不断的试路,但每一个分身的死亡都会减少我们的寿命(虽然我们拥有数以万年的生命,但终究不是不死之身)。
第七章,我们按照地图将整个天界(包括天外)划分成为很多方格区域,这样方便我们寻路探索。
第八章,我们从天山派出了四(八)个分身向四面(八方)出发,但由于神力有限只能一次控制一个分身去寻路探索。
1. 如果当前分身无法到达某个地方,就会返回本体,之后我们控制其他最靠近仙岛的分身(通过F 算法);
2. 如果分身遇到了远古萌兽或者其他危险,就会死亡,我们就知道了这个地方再也不用去了,之后我们控制其他最靠近仙岛的分身(通过F 算法);
3. 每当分身到达一个新的方格区域,则会再次分身为四(八)个,再次向周围的区域探索,之后我们控制其他最靠近仙岛的分身(通过F 算法);
4. 如果当前操控的分身遇到了其他分身,我们就用 F 算法 计算一下两个分身中那个分身到达这个方格区域更快一些(距离更短);
4.1 如果当前操作的分身比遇到的其他分身到这个方格区域快,则将其他分身返回本体,用当前操作的分身代替他继续寻路,之后我们控制其他最靠近仙岛的分身(通过F 算法);
4.2 如果是相反的,则将当前操作的分身返回本体,之后我们控制其他最靠近仙岛的分身(通过F 算法);
第九章,无上天君从仙界消失了,谁也不知道他究竟是找到了仙岛,还是没有找到,但最终所有的程序神猿都将无上天君视为情敌,立誓要杀他千万遍!
第十章(番外结局一),千辛万苦我们不断地这样分身寻找,分身寻找,最终我们找到了仙岛,见到了心意的仙女梦瑶,抱得美人归!
第十章(番外结局二),千辛万苦我们不断地这样分身寻找,分身寻找,最终我们探索完了天界所有的区域(方格),都没有找到去仙岛的路,有些区域我们没有探索,是因为太古萌兽以及天外绝地将这些地方包围起来或者分隔,这些成为了我们永远的痛,永远的痛!
代码界的程序神猿
随着科技的发展,计算机来临了,程序神猿们发现,我们可以用计算机模拟寻路,他们看到了去天外仙岛的希望,他们看到了仙女梦瑶。
下面就是他们通过计算机计算的方法(这是一篇网上的教程,我做了一些小小的改动与完善):
一、搜索区域
我们假设某个人要从A点到达B点,而一堵墙把这两个点隔开了,如下图所示,绿色部分代表起点A,红色部分代表终点B,蓝色方块部分代表之间的墙。
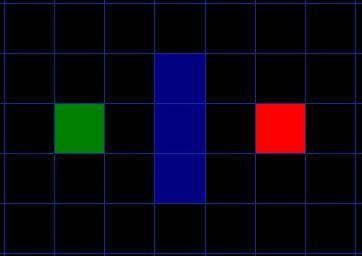
你首先会注意到我们把这一块搜索区域分成了一个一个的方格,如此这般,使搜索区域简单化,正是寻找路径的第一步。这种方法将我们的搜索区域简化成了一个普通的二维数组。数组中的每一个元素表示对应的一个方格,该方格的状态被标记为可通过的和不可通过的。通过找出从A点到B点所经过的方格,就能得到AB之间的路径。当路径找出来以后,这个人就可以从一个格子中央移动到另一个格子中央,直到抵达目的地。
这些格子的中点叫做节点。当你在其他地方看到有关寻找路径的东西时,你会经常发现人们在讨论节点。为什么不直接把它们称作方格呢?因为你不一定要把你的搜索区域分隔成方块,矩形、六边形或者其他任何形状都可以。况且节点还有可能位于这些形状内的任何一处呢?在中间、靠着边,或者什么的。我们就用这种设定,因为毕竟这是最简单的情况。
二、开始搜索
当我们把搜索区域简化成一些很容易操作的节点后,下一步就要构造一个搜索来寻找最短路径。在A*算法中,我们从A点开始,依次检查它的相邻节点,然后照此继续并向外扩展直到找到目的地。
我们通过以下方法来开始搜索:
1. 从A点开始,将A点加入一个专门存放待检验的方格的“开放列表”中。这个开放列表有点像一张购物清单。当前这个列表中只有一个元素,但一会儿将会有更多。列表中包含的方格可能会是你要途经的方格,也可能不是。总之,这是一个包含待检验方格的列表。
2.检查起点A相邻的所有可达的或者可通过的方格,不用管墙啊,水啊,或者其他什么无效地形,把它们也都加到开放列表中。对于每一个相邻方格,将点A保存为它们的“父方格”。当我们要回溯路径的时候,父方格是一个很重要的元素。稍后我们将详细解释它。
3. 从开放列表中去掉方格A,并把A加入到一个“封闭列表”中。封闭列表存放的是你现在不用再去考虑的方格。
此时你将得到如下图所示的样子。在这张图中,中间深绿色的方格是你的起始方格,所有相邻方格目前都在开放列表中,并且以亮绿色描边。每个相邻方格有一个灰色的指针指向它们的父方格,即起始方格。
<ignore_js_op>
接下来,我们在开放列表中选一个相邻方格并再重复几次如前所述的过程。但是我们该选哪一个方格呢?具有最小F值的那个。
三、路径排序
决定哪些方格会形成路径的关键是下面这个等式:
F = G + H
G=从起点A沿着已生成的路径到一个给定方格的移动开销。
H=从给定方格到目的方格的估计移动开销。这种方式常叫做试探,有点困惑人吧。其实之所以叫做试探法是因为这只是一个猜测。在找到路径之前我们实际上并不知道实际的距离,因为任何东西都有可能出现在半路上(墙啊,水啊什么的)。本文中给出了一种计算H值的方法,网上还有很多其他文章介绍的不同方法。
我们要的路径是通过反复遍历开放列表并选择具有最小F值的方格来生成的。本文稍后将详细讨论这个过程。我们先进一步看看如何计算那个等式。
如前所述,G是从起点A沿着已生成的路径到一个给定方格的移动开销,在本例中,我们指定每一个水平或者垂直移动的开销为10,对角线移动的开销为14。因为对角线的实际距离是2的平方根(别吓到啦),或者说水平及垂直移动开销的1.414倍。为了简单起见我们用了10和14这两个值。比例大概对就好,我们还因此避免了平方根和小数的计算。这倒不是因为我们笨或者说不喜欢数学,而是因为对电脑来说,计算这样的数字也要快很多。不然的话你会发现寻找路径会非常慢。
我们要沿特定路径计算给定方格的G值,办法就是找出该方格的父方格的G值,并根据与父方格的相对位置(斜角或非斜角方向)来给这个G值加上14或者10。在本例中这个方法将随着离起点方格越来越远计算的方格越来越多而用得越来越多。
有很多方法可以用来估计H值。我们用的这个叫做曼哈顿(Manhattan)方法,即计算通过水平和垂直方向的平移到达目的地所经过的方格数乘以10来得到H值。之所以叫Manhattan方法是因为这就像计算从一个地方移动到另一个地方所经过的城市街区数一样,而通常你是不能斜着穿过街区的。重要的是,在计算H值时并不考虑任何障碍物。因为这是对剩余距离的估计值而不是实际值(通常是要保证估计值不大于实际值――译者注)。这就是为什么这个方式被叫做试探法的原因了。想要了解更多些吗?
G和H相加就得到了F。第一步搜索所得到的结果如下图所示。每个方格里都标出了F、G和H值。如起点方格右侧的方格标出的,左上角显示的是F值,左下角是G值,右下角是H值。
<ignore_js_op>
我们来看看这些方格吧。在有字母的方格中,G=10,这是因为它在水平方向上离起点只有一个方格远。起点紧挨着的上下左右都具有相同的G值10。对角线方向的方块G值都是14。
H值通过估算到红色目标方格的曼哈顿距离而得出。用这种方法得出的起点右侧方格到红色方格有3个方格远,则该方格H值就是30。上面那个方格有4个方格远(注意只能水平和垂直移动),H就是40。你可以大概看看其他方格的H值是怎么计算出来的。
每一个方格的F值,当然就不过是G和H值之和了。
继续搜索
为了继续搜索,我们简单的从开放列表中选择具有最小F值的方格,然后对选中的方格进行如下操作:
将其从开放列表中移除,并加到封闭列表中。
检验所有的相邻方格,忽略那些不可通过的或者已经在封闭列表里的方格。如果这个相邻方格不在开放列表中,就把它添加进去。并将当前选定方格设为新添方格的父方格。
如果某个相邻方格已经在开放列表中了(意味着已经探测过,而且已经设置过父方格――译者),就看看有没有到达那个方格的更好的路径。也就是说,如果从当前选中方格到那个方格,会不会使那个方格的G值更小。如果不能,就不进行任何操作。相反的,如果新路径的G值更小,就将该相邻方格的父方格重设为当前选中方格。(在上图中是改变其指针的方向为指向选中方格。最后,重新计算那个相邻方格的F和G值。如果你看糊涂了,下面会有图解说明。
好啦,咱们来看看具体点的例子。在初始时的9个方块中,当开始方格被加到封闭列表后,开放列表里还剩8个方格。在这八个方格当中,位于起点方格右边的那个方格具有最小的F值40。所以我们选择这个方格作为下一个中心方格。下图中它以高亮的蓝色表示。
<ignore_js_op>
首先,我们将选中的方格从开放列表中移除,并加入到封闭列表中(所以用亮蓝色标记)。然后再检验它的相邻节点。那么在它紧邻的右边的方格都是墙,所以不管它们。左边挨着的是起始方格,而起始方格已经在封闭列表中了,所以我们也不管它。
其他四个方格已经在开放列表中,那么我们就要检验一下如果路径经由当前选中方格到那些方格的话会不会更好,当然,是用G值作为参考。来看看选中方格右上角的那一个方格,它当前的G值是14,如果我们经由当前节点再到达那个方格的话,G值会是20(到当前方格的G值是10,然后向上移动一格就再加上10)。为20的G值比14大,因此这样的路径不会更好。你看看图就会容易理解些。显然从起始点沿斜角方向移动到那个方格比先水平移动一格再垂直移动一格更直接。
当我们按如上过程依次检验开放列表中的所有四个方格后,会发现经由当前方格的话不会形成更好的路径,那我们就保持目前的状况不变。现在我们已经处理了所有相邻方格,准备到下一个方格吧。
我们再遍历一下开放列表,目前只有7个方格了。我们挑个F值最小的吧。有趣的是,目前这种情况下,有两个F值为54的方格。那我们怎么选择呢?其实选哪个都没关系,要考虑到速度的话,选你最近加到开放列表中的那一个会更快些。当离目的地越来越近的时候越偏向于选最后发现的方格。实际上这个真的没关系(对待这个的不同造成了两个版本的A*算法得到等长的不同路径)。
那我们选下面的那个好了,就是起始方格右边的,下图所示的那个。
<ignore_js_op>
这一次,在我们检验相邻方格的时候发现右边紧挨的那个是墙,就不管它了。上面挨着的那个也同样忽略。还有右边墙下面那个方格我们也不管。为什么呢?因为你不可能切穿墙角直接到达那个格子。实际上你得先向下走然后再通过那个方格。这个过程中是绕着墙角走。(注意:穿过墙角的这个规则是可选的,取决于你的节点是如何放置的。)
那么还剩下其他五个相邻方格。当前方格的下面那两个还不在开放列表中,那我们把它们加进去并且把当前方格作为它们的父方格。其他三个中有两个已经在封闭列表中了(两个已经在图中用亮蓝色标记了,起始方格,上面的方格),所以就不用管了。最后那个,当前方格左边挨着的,要检查一下经由当前节点到那里会不会降低它的G值。结果不行,所以我们又处理完毕了,然后去检验开放列表中的下一个格子。
重复这个过程直到我们把目的方格加入到开放列表中了,那时候看起来会像下图这个样子。
<ignore_js_op>
注意到没?起始方格下两格的位置,那里的格子已经和前一张图不一样了。之前它的G值是28并且指向右上方的那个方格。现在它的G值变成了20并且指向了正上方的方格。这个改变是在搜索过程中,它的G值被核查时发现在某个新路径下可以变得更小时发生的。然后它的父方格也被重设并且重新计算了G值和F值。在本例中这个改变看起来好像不是很重要,但是在很多种情况下这种改变会使到达目标的最佳路径变得非常不同。
那么我们怎样来自动得出实际路径的呢?很简单,只要从红色目标方格开始沿着每一个方格的指针方向移动,依次到达它们的父方格,最终肯定会到达起始方格。那就是你的路径!如下图所示。从A方格到B方格的移动就差不多是沿着这个路径从每个方格中心(节点)移动到另一个方格中心,直到抵达终点。简单吧!
<ignore_js_op>
A*算法总结
1.将开始节点放入开放列表(开始节点的F和G值都视为0);
2. 重复一下步骤
i. 在开放列表中查找具有最小F值的节点,并把查找到的节点作为当前节点;
ii. 把当前节点从开放列表删除, 加入到封闭列表;
Iii. 对当前节点相邻的每一个节点依次执行以下步骤:
① 如果该相邻节点不可通行或者该相邻节点已经在封闭列表中,则什么操作也不执行,继续检验下一个节点;
② 如果该相邻节点没有探测过,则将该节点添加到开放列表中, 并将该相邻节点的父节点设为当前节点,同时保存该相邻节点的G和F值;
③ 如果该相邻节点在开放列表中, 则判断若经由当前节点到达该相邻节点的G值是否小于原来保存的G值,若小于,则将该相邻节点的父节点设为当前节点,并重新设置该相邻节点的G和F值.
Iv. 循环结束条件:
① 当终点节点被加入到开放列表作为待检验节点时, 表示路径被找到,此时应终止循环;
② 当开放列表为空,表明已无可以添加的新节点,而已检验的节点中没有终点节点则意味着路径无法被找到,此时也结束循环;
3. 从终点节点开始沿父节点遍历, 并保存整个遍历到的节点坐标,遍历所得的节点就是最后得到的路径;
核心寻路类(AStar):
|
001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017
018
019
020
021
022
023
024
025
026
027
028
029
030
031
032
033
034
035
036
037
038
039
040
041
042
043
044
045
046
047
048
049
050
051
052
053
054
055
056
057
058
059
060
061
062
063
064
065
066
067
068
069
070
071
072
073
074
075
076
077
078
079
080
081
082
083
084
085
086
087
088
089
090
091
092
093
094
095
096
097
098
099
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
|
/* * 作 者:TKCB * 作者信息:身高(167cm+);体重(60kg±);年龄(90后);籍贯(陕西西安);星座(双鱼座);血型(O型);人生格言(The king come back.)。 * 交流学习:加QQ群[AS3殿堂之路](96759336),群里有无数主城、架构、妹子、LOL战友,欢迎交流讨论。 * 联系方式:QQ(2414268040);E-mail([url=mailto:tkcb@qq.com]tkcb@qq.com[/url]);手机(15029932353)。 */package seekRoute{ import flash.display.Sprite; import flash.display.Shape; /** * A*算法类 */ public class AStar extends Sprite { //************************ ************************* 属 性 ******************** *********** *** **//// /** 地图可通行数组,用于存放地图的可通行信息。数组元素为 0 表示可通行,数组元素为 1 表示是障碍地形 */ private var mapPassableArr : Array; /** 地图节点数组数组,用于存放所有节点(包括普通节点、开始节点、结束节点、障碍节点等等) */ private var mapNodalPointArr : Array; /** 开放列表 */ private var openList : Array; /** 开始节点 */ private var startNodalPoint : NodalPoint; /** 结束节点 */ private var endNodalPoint : NodalPoint; /** 是否结束寻路 */ public var isEnd : Boolean = false; /** 是否寻找到路线(寻路结果),true为寻找到了,false为没有寻找到 */ public var isRoute : Boolean = false; /** 找到的路线节点数组 */ public var routeArr : Array; /** 是否开启八方向寻路 */ public var isEight : Boolean = true; //************************ ************************* 构造函数 ******************** *********** *** **//// /** * 构造函数 */ public function AStar ( arr : Array ) { setSeekRouteMap ( arr ); } //************************ ************************* 方 法 ******************** *********** *** **//// /** * 设置新的寻路地图 */ public function setSeekRouteMap ( arr : Array ) : void { mapPassableArr = arr; mapNodalPointArr = []; var nodalPoint : NodalPoint; var i : int; var ilen : int = mapPassableArr.length; var j : int; var jlen : int = mapPassableArr[ 0 ].length; for ( i = 0; i < ilen; i++ ) { for ( j = 0; j < jlen; j++ ) { if ( mapNodalPointArr[ i ] == null ) { mapNodalPointArr[ i ] = []; } // 判断是否可以通行,并创建相应的节点 if ( mapPassableArr[ i ][ j ] == 0 ) { nodalPoint = new NodalPoint(); nodalPoint.num1 = i; nodalPoint.num2 = j; mapNodalPointArr[ i ][ j ] = nodalPoint; } else { nodalPoint = new NodalPoint(); nodalPoint.isPassable = false; nodalPoint.num1 = i; nodalPoint.num2 = j; mapNodalPointArr[ i ][ j ] = nodalPoint; } } } } /** * 寻找路线 * @param startNum1 开始节点,在地图中的竖向坐标(X轴)的索引值 * @param startNum2 开始节点,在地图中的横向坐标(Y轴)的索引值 * @param endNum1 结束节点,在地图中的竖向坐标(X轴)的索引值 * @param endNum2 结束节点,在地图中的横向坐标(Y轴)的索引值 */ public function seekRoute ( startNum1 : int, startNum2 : int, endNum1 : int, endNum2 : int ) : void { trace( "寻找路线!!!" ); isRoute = false; routeArr = null; openList = []; //// 将传入的开始点位置对应的节点设为开始节点,将传入的结束点位置对应的节点设为结束节点 startNodalPoint = mapNodalPointArr[ startNum1 ][ startNum2 ]; endNodalPoint = mapNodalPointArr[ endNum1 ][ endNum2 ]; startNodalPoint.isStart = true; endNodalPoint.isEnd = true; //// 核心步骤【1】:将开始节点加入开放列表 openList[ 0 ] = startNodalPoint; openList[ 0 ].inOpenList = true; //// 核心步骤【2】:不断的检测开放列表中的节点 while ( isEnd == false ) { //——trace( "循环探测中……" ); var i : int; var ilen : int; var j : int; var jlen : int; var currentNP : NodalPoint; // 当前节点 var currentNum : int; // 当前节点在开放列表中的索引位置 //// 核心步骤【2.1】:在开放列表中查找具有最小 F 值的节点,并把查找到的节点作为当前节点 ilen = openList.length; currentNP = openList[ 0 ]; currentNum = 0; for ( i = 0; i < ilen; i++ ) { if ( openList[ i ].F < currentNP.F ) { currentNP = openList[ i ]; currentNum = i; } } //// 核心步骤【2.2】:把当前节点从开放列表删除, 加入到封闭列表 currentNP.inOpenList = false; openList[ currentNum ] = openList[ openList.length - 1 ]; openList.pop(); //// 核心步骤【2.3】:对当前节点相邻的每一个节点依次执行以下步骤: //// 下面是一个九宫格循环,横向和竖向分别循环三次 var currentDetectNP : NodalPoint; // 当前要被探测的节点 var num1 : int; // 被探测节点的竖向坐标索引 var num2 : int; // 被探测节点的横向坐标索引 var GNum : int; // 用于计算 G 值 var FNum : int; // 用于计算 F 值 ilen = 2; jlen = 2; for ( i = -1; i < ilen; i++ ) { for ( j = -1; j < jlen; j++ ) { //// 如果关闭了八方向寻路(即为四方向寻路),则忽略掉左上、左下、右上、右下的四个节点的探路 if ( isEight == false ) { // 左上角节点 if ( i == -1 && j == -1 ) continue; // 右上角节点 if ( i == -1 && j == 1 ) continue; // 左下角节点旁边障碍物判断 if ( i == 1 && j == -1 ) continue; // 右下角节点旁边障碍物判断 if ( i == 1 && j == 1 ) continue; } //// 核心步骤【2.3.1】:如果该相邻节点不可通行或者该相邻节点已经在封闭列表中,则什么操作也不执行,继续检验下一个节点 GNum = 10; // 设置 G 值 num1 = currentNP.num1 + i; num2 = currentNP.num2 + j; //// 各种不需要检测的情况…… if ( i == 0 && j == 0 ) { //——trace( "探测的点为当前节点!!!" ); continue; } if ( num1 < 0 ) { //——trace( "探测的点超出上边!!!" ); continue; } if ( num1 == mapNodalPointArr.length ) { //——trace( "探测的点超出下边!!!" ); continue; } if ( num2 < 0 ) { //——trace( "探测的点超出左边!!!" ); continue; } if ( num2 == mapNodalPointArr[ 0 ].length ) { //——trace( "探测的点超出右边!!!" ); continue; } //// 从节点数组中获取当前要探测的节点 currentDetectNP = mapNodalPointArr[ num1 ][ num2 ]; if ( currentDetectNP.isStart ) { //——trace( "该节点为开始点!!!" ); continue; } if ( currentDetectNP.isPassable == false ) { //——trace( "该节点不可通行!!!" ); continue; } if ( currentDetectNP.inCloseList ) { //——trace( "该节点在封闭列表中!!!" ); continue; } // 左上角节点旁边障碍物判断 if ( i == -1 && j == -1 ) { if ( mapNodalPointArr[ num1 + 1 ][ num2 ].isPassable == false ) { //——trace( "【左上角】该节点的下边有障碍物!!!" ); continue; } if ( mapNodalPointArr[ num1 ][ num2 + 1 ].isPassable == false ) { //——trace( "【左上角】该节点的右边有障碍物!!!" ); continue; } GNum = 14; // 设置 G 值 } // 右上角节点旁边障碍物判断 if ( i == -1 && j == 1 ) { if ( mapNodalPointArr[ num1 + 1 ][ num2 ].isPassable == false ) { //——trace( "【右上角】该节点的下边有障碍物!!!" ); continue; } if ( mapNodalPointArr[ num1 ][ num2 - 1 ].isPassable == false ) { //——trace( "【右上角】该节点的左边有障碍物!!!" ); continue; } GNum = 14; // 设置 G 值 } // 左下角节点旁边障碍物判断 if ( i == 1 && j == -1 ) { if ( mapNodalPointArr[ num1 - 1 ][ num2 ].isPassable == false ) { //——trace( "【左下角】该节点的上边有障碍物!!!" ); continue; } if ( mapNodalPointArr[ num1 ][ num2 + 1 ].isPassable == false ) { //——trace( "【左下角】该节点的右边有障碍物!!!" ); continue; } GNum = 14; // 设置 G 值 } // 右下角节点旁边障碍物判断 if ( i == 1 && j == 1 ) { if ( mapNodalPointArr[ num1 - 1 ][ num2 ].isPassable == false ) { //——trace( "【右下角】该节点的上边有障碍物!!!" ); continue; } if ( mapNodalPointArr[ num1 ][ num2 - 1 ].isPassable == false ) { //——trace( "【右下角】该节点的左边有障碍物!!!" ); continue; } GNum = 14; // 设置 G 值 } //// 核心步骤【2.3.2】:如果该相邻节点没有探测过,则将该节点添加到开放列表中, 并将该相邻节点的父节点设为当前节点,同时保存该相邻节点的G和F值 if ( currentDetectNP.isDetect == false ) { //——trace( "普通节点" ); currentDetectNP.isDetect = true; // 设置为被探测过 currentDetectNP.inOpenList = true; // 加入开放列表 openList.push( currentDetectNP ); // 加入开放列表 currentDetectNP.parentNodalPoint = currentNP; // 设置父节点 // 设置 G 值 currentDetectNP.G = currentNP.G + GNum; // 设置 H 值 currentDetectNP.H = ( Math.abs( currentDetectNP.num1 - endNodalPoint.num1 ) + Math.abs( currentDetectNP.num2 - endNodalPoint.num2 ) ) * 10; // 设置 F 值 currentDetectNP.F = currentDetectNP.G + currentDetectNP.H; } //// 核心步骤【2.3.3】:如果该相邻节点在开放列表中, 则判断若经由当前节点到达该相邻节点的G值是否小于原来保存的G值,若小于,则将该相邻节点的父节点设为当前节点,并重新设置该相邻节点的G和F值 if ( currentDetectNP.inOpenList ) { //——trace( "开放列表中的节点!!!" ); FNum = currentNP.G + GNum + ( ( Math.abs( currentDetectNP.num1 - endNodalPoint.num1 ) + Math.abs( currentDetectNP.num2 - endNodalPoint.num2 ) ) * 10 ) if ( FNum < currentDetectNP.F ) { currentDetectNP.parentNodalPoint = currentNP; // 设置父节点 // 设置 G 值 currentDetectNP.G = currentNP.G + GNum; // 设置 F 值 currentDetectNP.F = currentDetectNP.G + currentDetectNP.H; } } //// 核心步骤【2.4.1】:循环结束条件:当结束节点被加入到开放列表作为待检验节点时,表示路径被找到,此时应终止循环 if ( currentDetectNP.isEnd ) { //——trace( "寻路结束,找到了路线!" ); isEnd = true; // 寻路结束 isRoute = true; // 找到了路线 routeArr = []; routeArr.push( currentDetectNP ); //// 核心步骤【3】:从终点节点开始沿父节点遍历, 并保存整个遍历到的节点坐标,遍历所得的节点就是最后得到的路径 while ( true ) { if ( currentDetectNP.parentNodalPoint.isStart == false ) { routeArr.push( currentDetectNP.parentNodalPoint ); currentDetectNP = currentDetectNP.parentNodalPoint; } else { break; } } } } } //// 核心步骤【2.4.2】:循环结束条件:开放列表为空,表明已无可以添加的新节点,而已检验的节点中没有终点节点则意味着路径无法被找到,此时也结束循环 if ( openList.length == 0 ) { //——trace( "寻路结束,没有找到路线!" ); routeArr = []; isEnd = true; // 寻路结束 isRoute = false; // 没有找到路线 } } } }} |
--------------------------------------------------------------------------我是分界线--------------------------------------------------------------------