树的遍历和堆排序

1、二叉树的遍历

　　遍历，迭代所有的元素以便

　　树的遍历：对数中所有元素不重复放入访问一遍，也成为扫描（非线性变成线性结构）

　　遍历方式：　　　　

　　　　广度优先遍历：

　　　　　　　层序遍历

　　　　深度优先遍历：

　　　　　　　 前序遍历

　　　　　　　中序遍历

　　　　　　　后序遍历

　　　　遍历序列：将树中所有元素遍历一遍后，得到的匀速的序列，将层次结构转换为了线性结构。

　　2.1 层序遍历：

　　　　

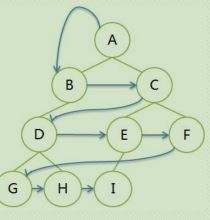
　　　　　　遍历序列：ABCDEFGHI　　

　　2.2、深度优先遍历：

　　　　　设树的根结点为D， 左子树为L，右子树为R， 且要求L一定在R之前，则：

　　　　　　前序遍历：也叫先序遍历，先根遍历：DLR

　　　　　　中序遍历：中根遍历：LDR

　　　　　　后序遍历：后根遍历：LRD

　　　　2.2.1：前序遍历：

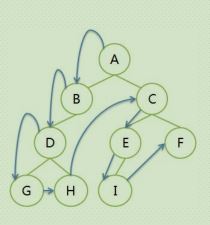
　　　　　　　　遍历序列： A BDGH CEIF

　　　　2.2.2 中序遍历：

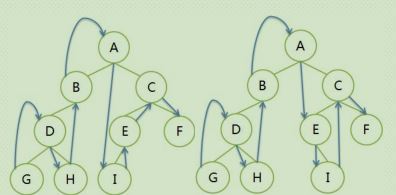
　　　　　　　　　　遍历序列：

　　　　　　　　　　　　　　左图：GDHB A IECF      I 是左子树

　　　　　　　　　　　　　　右图：GDHB A EICF　　I 是右子树

　　　　2.2.3：后序遍历：

　　　

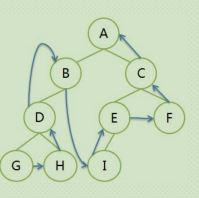
　　　　　　　　　　遍历序列：GHDB IEFC A

　　　　　　　　　　　　　　　　　　　　　

2、堆排序 Heap Sort

　　堆Heap

　　　　堆是一个完全二叉树　　　　　　

　　　　每个非叶子结点都要大于或者等于其左右孩子结点的值，称为大顶堆

　　　　每个非叶子结点都要小于或者等于其左右孩子结点的值，称为小顶堆

　　　　根结点一定是大顶堆中的最大值，一定是小顶堆中的最小值。

　　大顶堆：

　　　　完全二叉树的每一个非叶子结点都要大于或者等于其左右孩子结点的值称为大顶堆

　　　　根结点一定是大顶堆中的最大值

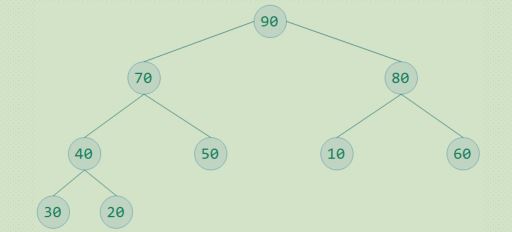
　　小顶堆：

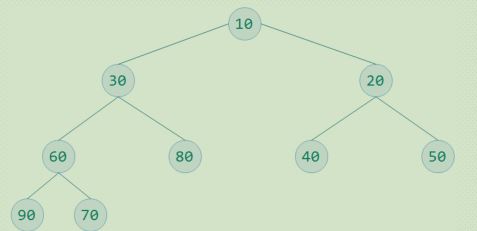
　　　1步：构建完全二叉树：

　　　　　　待排序数字为30,20,80,40,50,10,60,70,90

　　　　　　构建一个完全二叉树存放数据，并根据性质5（2*i+ 1）对元素编号，放入顺序的数据结构总

　　　　　　构造一个列表为：[0, 30,20,80,40,50,10,60,70,90] #补了一个零，主要是30对应的i 从1 开始！

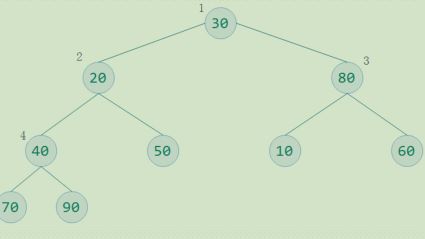
　　2步：构建大顶堆------核心算法

　　　　　　度数为2的结点A ，如果他的左右孩子结点的最大值比他大的，将这个最大值和该结点交换

　　　　　　度数为1 的结点A，如果他的左孩子的值大于它，则交换

　　　　　　如果结点A 被交换到新的文职，还要和其孩子结点重复上面的过程。

　　　　起点结点的选择：

　　　　　　从完全二叉树的最后一个节点的额双亲结点开始，即最后一层的最右边叶子节点的父结点开始

　　　　　　结点数为n，则其实结点的编号为 n//2

　　　　下一个节点的选择：

　　　　　　从其实结点开始想左找其同层结点，到头后再从上一层的最右边结点开始继续向左诸葛查找，直至根结点

　　　　大顶堆的目标：

　　　　　　确保每个结点的都比左右结点的值大

　　3、排序：

　　　　将大顶堆根结点这个最大值和最后一个叶子结点交换， 那么最后一个叶子结点就是最大值，将这个叶子结点排除在待排序结点之外。

　　　　从根结点开始（新的根结点），重新调整为大顶堆后，重复上一步。

　　

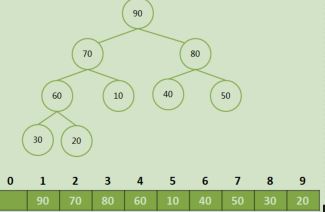
　　　　堆顶和最后一个节点交换，并排除最后一个节点：

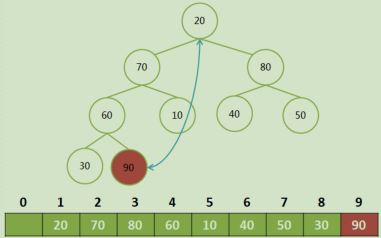
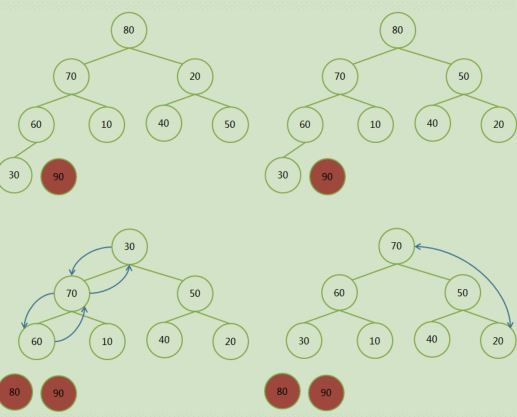
 代码实现：

import math

def print_tree(origin):
    index = 2 ** h - 1  # 满树的总节点数 15
    for i in range(1,h+1):
        times = 2 ** (i - 1)
        for j in range(times - 1, times * 2 - 1):
            if j >= length: break
            # print(index)
            print('{:^{}}'.format(origin[1:][j], index*2),end='  '*1)
        print()
        index //=  2

# origin = [30, 20, 80, 40, 50, 10, 60, 70, 90]
origin = [0,30, 20, 80, 40, 50, 10, 60, 70, 90]
length = len(origin)-1  # 节点 9
h = math.ceil(math.log(length, 2))  # >3  所以深度为4
# print_tree(origin)

# 只调了一个元素：90
def heap_adjust(origin, length,i):
    while 2 * i <= length:
        l_child = 2 * i
        max_child = l_child
        if  length > l_child and origin[l_child + 1] > origin[l_child]:
            max_child = l_child + 1

        if origin[max_child] > origin[i]:
            origin[i], origin[max_child] = origin[max_child], origin[i]
            i = max_child
        else:
            break
    return origin
# heap_adjust(origin, length, i = length // 2)
# print(origin)
# print_tree(origin)

# 构建大顶堆
def max_heap(length, origin):
    for i in range(length//2, 0, -1):
        heap_adjust(origin, length, i)
        print("********************************")
        print(origin)
        print_tree(origin)
    return origin
print_tree(max_heap(length, origin))


# 排序：
def sort(length, origin):
    while length > 1 :
        origin[1],origin[length] = origin[length], origin[1]
        length  -=  1
        heap_adjust(origin,length, 1) 
        # 因为当大顶堆构建完后，事实上，次大值，就在第二层，所以，每次只在一层二层进行比较获取大顶堆
    return origin

print(sort(length, origin))

结果截图：

改进：如果最后剩两个元素的时候，如果后一个节点比堆顶大，就不用再调整了！！！

 总结：

　　是利用堆性质的一种选择排序，在堆顶选出最大值或者最小值

　　时间复杂度：

　　　　堆排序的时间复杂度O(nlogn)

　　　　由于堆排序队员是记录的排序的状态并不敏感，因此它无论是最好，最坏，和平均时间复杂度均为O（nlongn)）

　　　　

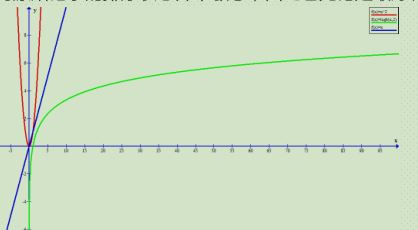
 　　从图中可以看出比之前的交换，插入排序要好的多的多的

 　　空间复杂度：将原序列 加了一个0，中间加了一个变量调了一下，新的序列

　　　　　　　　只使用了一个交换空间，空间复杂度就是O（1） hash（）也是O（1）

 　　　　　　　　不稳定的排序算法