LeetCode:数组（四）

本组囊括数组相关题目，且只包括两道有关数学的问题。

1. Two Sum

题目描述：简单

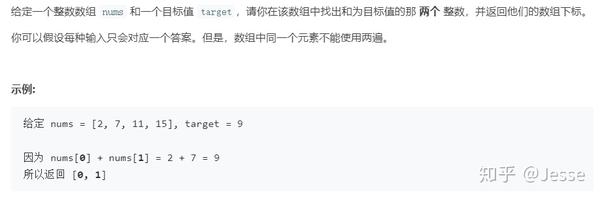
首先可以想到暴力解法，很简单，遍历每个元素x，并查找是否存在一个值与target - xt相等的目标元素。

时间复杂度：O(n^2)：对于每个元素，我们试图通过遍历数组的其余部分来寻找它所对应的目标元素，这将耗费 O(n) 的时间。因此时间复杂度为 O(n^2)，空间复杂度：O(1)。

为了对运行时间复杂度进行优化，我们需要一种更有效的方法来检查数组中是否存在目标元素。如果存在，我们需要找出它的索引。保持数组中的每个元素与其索引相互对应的最好方法是什么？哈希表。
在python中用字典实现这一功能，即数组索引对应值，数组值对应键。
实际上最优方式选取一遍哈希表，即在遍历一遍数组将值和索引放进字典的同时，查找是否target-n在字典的键中。
时间复杂度：O(n)，我们只遍历了包含有 n个元素的列表一次。在表中进行的每次查找只花费 O(1) 的时间。
空间复杂度：O(n)，所需的额外空间取决于哈希表中存储的元素数量，该表最多需要存储 n 个元素。

解法一：

class Solution(object):
    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        #为了对运行时间复杂度进行优化，我们需要一种更有效的方法来检查数组中是否存在目标元素。如果存在，我们需要找出它的索引。保持数组中的每个元素与其索引相互对应的最好方法是什么？哈希表。
        # 在python中用字典实现这一功能，即数组索引对应值，数组值对应键。
        # 实际上最优方式选取一遍哈希表，即在遍历一遍数组将值和索引放进字典的同时，查找是否target-n在字典的键中。
        # 时间复杂度：O(n)
        # 我们只遍历了包含有 nn个元素的列表一次。在表中进行的每次查找只花费 O(1) 的时间。
        # 空间复杂度：O(n)，
        # 所需的额外空间取决于哈希表中存储的元素数量，该表最多需要存储 n 个元素。
        dic = {}
        for i,n in enumerate(nums):
            if target - n in dic:
                return [dic[target-n], i]
            dic[n] = i

167. Two Sum II - Input array is sorted

题目描述：简单

和上一题的要求几乎一模一样，只是这里给出的数组是有序且按升序排好的。

首先，我们当然可以使用上一题的思路：一是暴力解法，这样时间复杂度太高，二是利用哈希表来求解，但这样也会引入额外的复杂度。

其次，看到题目提到有序数组，即可想到双指针的方法，这里就不是用的同向指针了，而是一个指向开头一个指向结尾的指针，两边向中间靠拢，有点类似于二分查找。使p+q等于目标值，即返回;若大于，则q--；若小于，则p++。
但是要注意边界条件，不同于二分查找，假设这里的指针分别设为p和q，循环终止条件不应设为p<=q，而应该为p<q，这样就不会存在本来p+q不存在与数组中而找到了这个一个数的问题。

解法一：

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        # 首先我们可以使用之前的暴力解法或哈希解法，但是都没有用到题中数组有序的条件
        # 看到有序，考虑双指针，这里就不是用的同向指针了，而是一个指向开头一个指向结尾的指针，两边向中间靠拢，有点类似于二分查找。使p+q等于目标值，即返回;若大于，则q--；若小于，则p++。
        # 但是要注意边界条件，不同于二分查找，假设这里的指针分别设为p和q，循环终止条件不应设为p<=q，而应该为p<q，这样就不会存在本来p+q不存在与数组中而找到了这个一个数的问题。
        # 解法一
        p = 0
        q = len(numbers) - 1
        while p < q: # 注意边界
            if numbers[p] + numbers[q] == target:
                return [p+1, q+1]
            elif numbers[p] + numbers[q] < target:
                p += 1 
            else:
                q -= 1
        return None # 循环完仍未找到答案