2019.01.19-THUWC2019模拟2019.1.16-permutation

 

题目描述：

算法标签：推式子，组合数的一些性质

思路：

考虑满足第一个条件的方案数，对于任意一种排列，前1-y中每一位为前y位最大值的概率均等，所以第y位为前y为最大值的方案数为

考虑第二个条件，任选两个不同的数位x,y，2*Px<2*Py的概率和2*Px>2*Py的概率相等，所以我们如果求出2*Px=Py的方案数，就能求出满足第二个条件的方案数。

令f[x]表示满足条件1 且2*Px=Py的方案数。

则

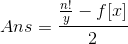
考虑计算f[x]

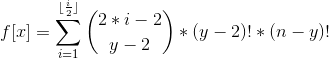
因为后半部分均与i无关，我们令

 

考虑如何递推求g[x]。

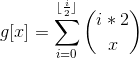
观察组合数的杨辉三角图，发现

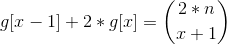
于是就可以递推O(n)求g[x]了，求ans的问题就迎刃而解了。

以下代码：

#include<bits/stdc++.h>
#define il inline
#define LL long long
#define _(d) while(d(isdigit(ch=getchar())))
using namespace std;
const int N=1e6+5,p=998244353;
int n,q,g[N],jc[N],ny[N],inv2,m;
il int read(){
    int x;char ch;
    _(!);x=ch^48;
    _()x=(x<<1)+(x<<3)+(ch^48);
    return x;
}
il int ksm(LL a,int y){
    LL b=1;
    while(y){
        if(y&1)b=b*a%p;
        a=a*a%p;y>>=1;
    }
    return b;
}
il int mu(int x,int y){
    if(x+y>=p)return x+y-p;
    return x+y;
}
il int C(int n,int m){
    return 1ll*jc[n]*ny[m]%p*ny[n-m]%p;
}
int main()
{
    freopen("permutation.in","r",stdin);
    freopen("permutation.out","w",stdout);
    n=read();q=read();inv2=ksm(2,p-2);m=n>>1;
    jc[0]=1;
    for(int i=1;i<=n;i++)jc[i]=1ll*jc[i-1]*i%p;
    ny[n]=ksm(jc[n],p-2);
    for(int i=n;i;i--)ny[i-1]=1ll*ny[i]*i%p;
    g[0]=m;
    for(int i=1;i<=n-2;i++)g[i]=1ll*mu(C(m<<1,i+1),p-g[i-1])*inv2%p;
    while(q--){
        read();int y=read();
        int res=1ll*g[y-2]*jc[y-2]%p*jc[n-y]%p;
        res=mu(p-res,1ll*jc[n]*ksm(y,p-2)%p);
        printf("%d
",1ll*res*inv2%p);
    }
    return 0;
}