复习一下排序算法

因为找实习时候碰见笔试题出算法题的，在这里复习一下学习过的排序算法的思路。（以数组理思路）

---

算法性能：

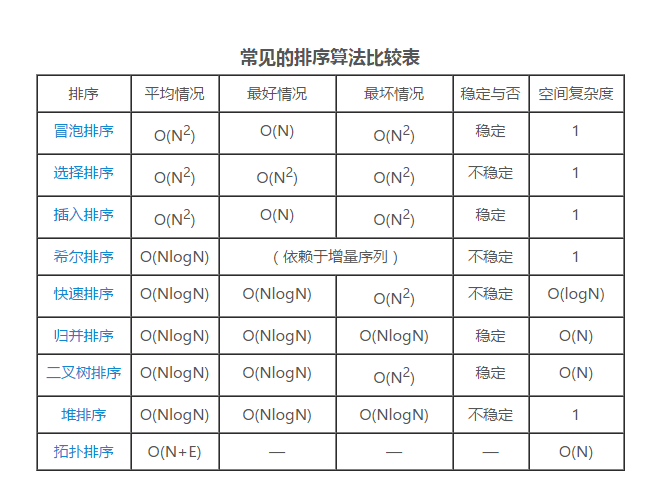
算法的稳定性：如果A_i = A_j，排序前A_i在A_j之前，排序后A_i还在A_j之前，则称这种排序算法是稳定的

  

---

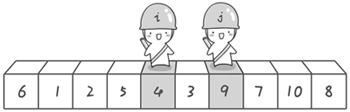
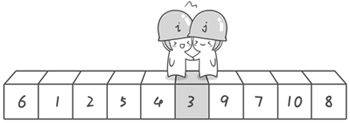
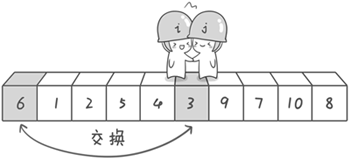
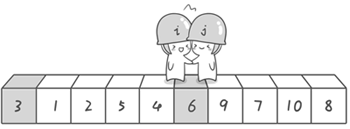
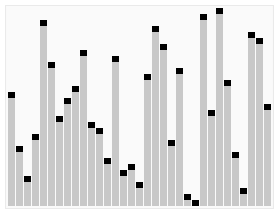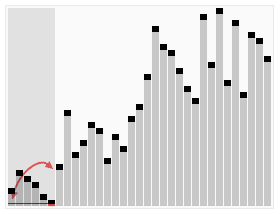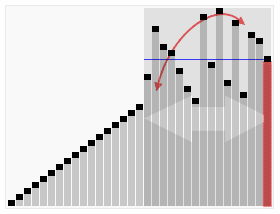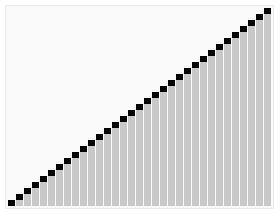
冒泡排序：

1. 比较相邻的元素，如果前一个比后一个大/小，就把它们两个调换位置。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大/小的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

效果展示：

 

---

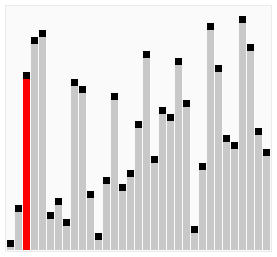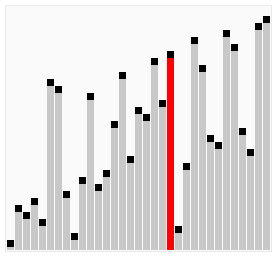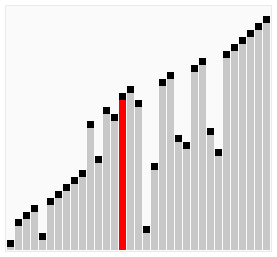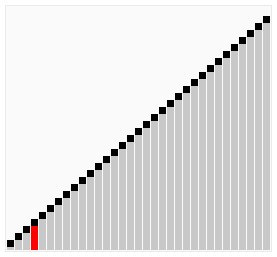
 选择排序：

选择排序就是，先查找数组中最大（最小）的元素，将其置换到初始位置，接着在剩下的元素中查找其中最大（最小）的元素，将其置换到之前那个元素之后，以此类推，直到所有元素均排序完毕。

---

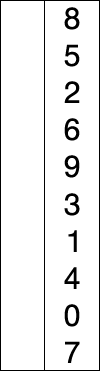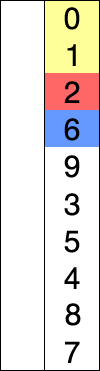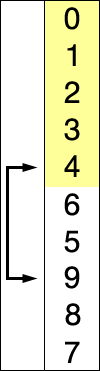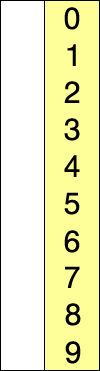
插入排序：

插入排序利用的是，在数组中第P个元素调整位置时，前面的p-1个元素都已经排序完毕。

算法的实现（此处以升序为例）：

1. 默认数组第一个元素已排好序，从第二个元素开始取并将待排序的元素赋予一个临时表，若a[1]<a[0]，则将a[0]往后挪，将位置让出来方便临时变量插入，即令此时的a[1]=a[0]（a[1]的值已经赋予临时变量）。
2. 前面两个元素排好序后，取第三个元素（将其赋予临时变量）从后往前与前面的元素比较，若前面的元素大于它，需向后挪位置。以此类推，知道最后一个元素插入完毕。

 for (int i = 1; i < n; i++)         // 取需要排序的目标元素
    {
        int get = A[i];                 // 将这个目标待排序的赋予临时变量
        int j = i - 1;                  // 从后往前开始比较
        while (j >= 0 && A[j] > get)    
        {
            A[j + 1] = A[j];            // 如果被比较的比目标大，就将其右移
            j--;
        }
        A[j + 1] = get; // 直到被比较的元素比目标元素小(或二者相等)，将目标元素插入该元素右边(相等元素的相对次序未变，所以插入排序是稳定的)
    }

---

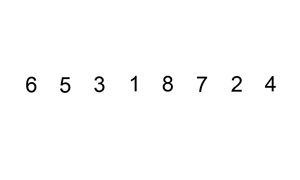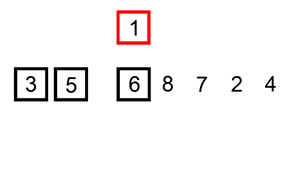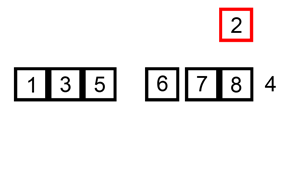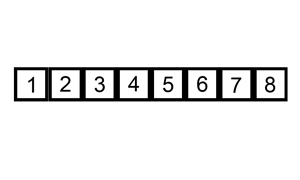
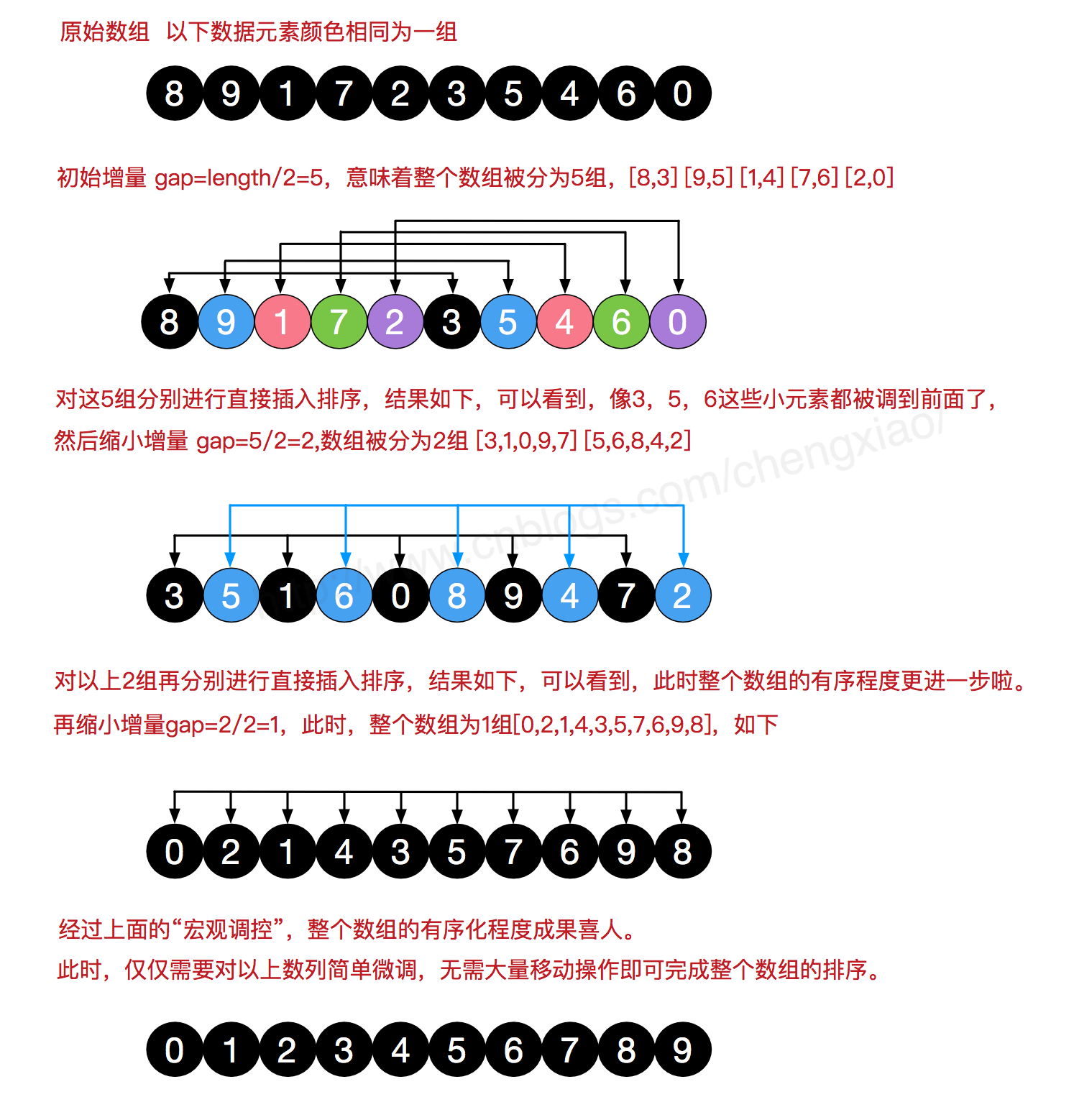
希尔排序：

希尔排序使用一个序列h₁，h₂，h₃，……h_k，只要h₁=1（即最简单的插入排序），任何的增量序列都是可行的。在使用增量序列h_k进行排序时，将每隔h_k的元素看成一个区间，忽略其他元素，将其排序，而并在他们实际的位置上进行交换。

 

---

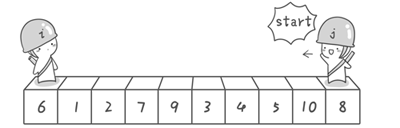
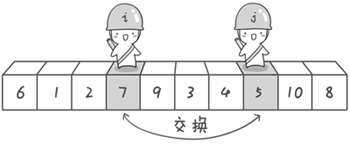
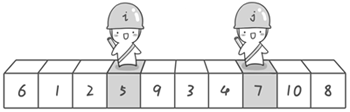
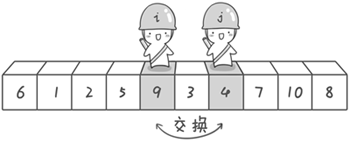
快速排序（以升序为例）：

1. 如果数组元素为0或1，则返回；
2. 任取数组中一元素V，将其设为枢纽元(pivot)
3. 将数组中的剩余元素划分成大于V和小于V两部分
4. 划分的部分重复上述操作，直至为1的情况。

设置两个指针，left和right,left从左往右找比枢纽元大的数，找到即停止，right从右往左依次找比枢纽元小的数，找到即停止，如果此时，left对应的数组下标小于right的，则两者对应的数组元素交换位置。交换位置后，两指针继续查找，当到left与right相遇，left停止查找，此时若right对应的元素若依旧大于枢纽元，则right继续查找，找到符合要求的元素后与枢纽元交换位置即可。此时枢纽元左边都是小于它的数，右边都是大于它的数，再对划分好的区域重复上述操作，即可排序完毕。