链接:LCT总结——应用篇(附题单)(LCT)
链接:Link-Cut-Tree
链接:LCT
LCT(Link-Cut-Tree),树套Splay。实链剖分维护森林。支持连边删边。认父不认子。
(notroot):是否为Splay的根,是则返回0,否则返回1。我们搞一个 (notroot) 主要是因为当某个节点为根的时候,会有一些不一样的地方,比如根虽然有 (fa),但是一般情况下不可以动这个 (fa),因为它是另一棵 (Splay) 上的点。
(splay):把 (cur) 旋转至当前 (Splay) 的根。
(Access):把 (cur) 一直到整棵树的根打通成一条实链。
(make ~ root):将 (cur) 设置为当前树的根(通过打翻转标记实现)
(find ~ root):返回 (cur) 所在的树的根,顺便把 (cur) 给 (Access)。
(Split):提取出 (x -> y) 一条链。其中 (x) 为根(深度最浅), (y) 在 (x) 的(Splay) 中,且为 (Splay) 的根。见图:
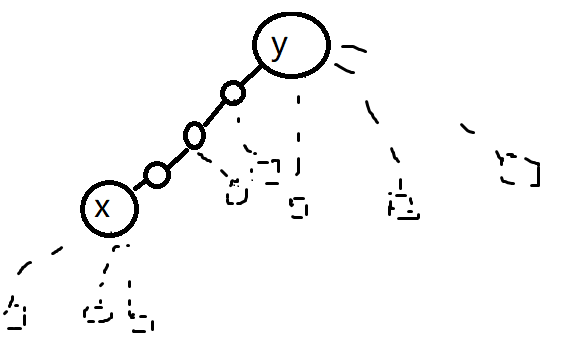
(Link):将 (x, y) 相连(如果已经联通就忽视)
(Cut):将边 ((x, y)) 删除(如果没有则忽视)
例题:
P3690 【模板】Link Cut Tree (动态树)
P2147 [SDOI2008]洞穴勘测
此题保证Link和Cut合法,可以学一下这个的写法。
P1501 [国家集训队]Tree II
需要打区间加法、乘法标记(与线段树类似)。
保证Link和Cut合法。
P3950 部落冲突
P4332 [SHOI2014]三叉神经树
lct维护叶子到根的路径信息。动态树维护静态树
这里有一个问题:我打区间赋值的lazy标记就会WA20,如果打区间加的lazy标记就能AC。可是我明明已经保证该区间内的值都相同了啊,这两种方法有什么不同?
动态维护最小生成树:
P4172 [WC2006]水管局长
题意:
给一张简单无向图。支持删边,和求 (x) 到 (y) 的路径中边权最大的一条边的边权最小是多少。
题解:
如果要支持的是加边,那么我们维护一个最小生成树森林。每次我们加一条边,如果没有环,就加;如果构成环,且环上的最大边权比该边小,就不管这条边;如果环上的最大边权比该边大,就删掉那条边,加上这一条边。
只删边的话离线逆序处理就好。
由于要迅速找到一条路径上的最大边权,一种比较好的方法为化边为点,每个点维护 (val,mxid)(val:如果是点,则设置一个不影响的值,如0或者-inf)(mxid:子树中的最大点权)。同时为了方便找到每条边所连的点,对于每一条边要维护 (U, V)。然后就lct经典操作了。
处理边的时候注意一下要不要+n。
P4234 最小差值生成树
确定最小值后转化成求合法边的最小生成树。
将边从大到小排序后动态维护最小生成树即可。
思想:类似“换根dp”的思想:确定一种情况的答案,再迅速地去切换所有情况。
类似的题目:P2387 [NOI2014]魔法森林
P4180 [BJWC2010]严格次小生成树
维护次大值,模拟克鲁斯卡尔,查环即可。
维护边双:
P2542 [AHOI2005]航线规划
(思路是参考lhm_大佬的代码得出的)
只支持动态加边。
仍然为化边为点的思想。
初始化所有代表边的点为边双。若加边不构成环,则加。否则,不加,且将环上的所有的点都标记为“非桥".(懒标记搞)(这里主要是代表边的点,只不过顺便把其它点也标记了)
两点间的桥的数量可以维护Splay的子树桥的数量,直接Split后得出。
2959: 长跑
题意:
支持单点修改,连边,查两边双间的(边双树)链上权值和。
题解:
这次不化边为点了,如果构成环,直接Dfs缩点即可。
可能会造成某些点的 (fa) 指空,因此需要额外维护一个边双并查集,每次找 (fa) 都改为找 (find(fa)) (son不会指空,因为我们都只会在边双代表点的信息上修改,缩点前 (Split) 不会影响 (son) 的准确性;随点后暴力DFS后新的边双代表点无 (son),单独为一棵辅助树)
双倍经验:#4998. 星球联盟 my record
维护原图的子树
每个点把所有的虚儿子的信息也附加上就好了。在涉及修改边的实虚的时候需要格外注意。
然而没有那么简单。lct只支持维护子树信息,不支持修改子树信息。因此涉及子树而不涉及加边删边的题还是用树链剖分做更方便。
注意:只涉及到pushup,access,link,不涉及cut,因为cut实际上删的实儿子
//siz : 仅包含所有虚儿子的信息(信息以大小为例)
//Siz : 包含子树信息(含自身,实儿子,虚儿子)
inline void pushup(int cur) {
Siz[cur] = siz[cur] + Siz[son[cur][0]] + Siz[son[cur][1]] + 1;
}
inline void Access(int cur) {
for (register int p = cur, lst = 0; p; lst = p, p = fa[p])
splay(p), siz[p] += Siz[son[p][1]], son[p][1] = lst,
siz[p] -= Siz[son[p][1]], pushup(p);
}
inline void Link(int x, int y) {
make_root(x);
make_root(y);
fa[x] = y, siz[y] += Siz[x];
}
应用:动态维护重心:P4299 首都
附
错误记录
错误1:
inline void Link(int x, int y) {
make_root(x);
fa[x] = y;
//pushup(y);
}
主要是因为这里加的是虚边,不需pushup。而我们只保证x被splay过了,也就只保证x的信息是完全正确的。y的信息可能由于祖先的标记未被下放而出现错误。
错误2:
//动态维护最小生成树
inline void Try(int x, int y, int id) {
int xx = find(x), yy = find(y);
if (xx != yy) {
Link(x, id + n);
Link(id + n, y);
//不是 Link(x, y) !!
FA[xx] = yy;
return ;
}
Split(x, y);
int Md = mxid[y], md = Md - n, Id = id + n;
if (val[Md] < val[Id]) return ;
Cut(Md, X[md]), Cut(Md, Y[md]);
Link(Id, X[id]), Link(Id, Y[id]);
}
错误3:
inline void make_root(int cur) {
Access(cur), splay(cur), pushrev(cur);
//不是 make_root(cur); 否则会无限递归
}
错误4:
inline void splay(int cur) {
int p = cur;
while (notroot(p)) stk[++stop] = p, p = fa[p];
//Attention : p = fa[p];
stk[++stop] = p;
while (stop) pushdown(stk[stop--]);
for (register int faa = fa[cur]; notroot(cur); rotate(cur), faa = fa[cur])
if (notroot(faa)) rotate(get_which(cur) == get_which(faa) ? faa : cur);
pushup(cur);
}
错误5:
inline void rotate(int cur) {
int faa = fa[cur], fafa = fa[faa];
bool flag = get_which(cur);
fa[cur] = fafa; if (notroot(faa)) son[fafa][get_which(faa)] = cur;
son[faa][flag] = son[cur][flag ^ 1]; if (son[cur][flag ^ 1]) fa[son[cur][flag ^ 1]] = faa;
son[cur][flag ^ 1] = faa; fa[faa] = cur;
//pushup(cur); <-不能只pushup(cur)
pushup(faa);
}
错误6:
inline void Link(int x, int y) {
//make_root(x), fa[y] = x;
make_root(x), fa[x] = y;
}
错误7:
inline bool notroot(int cur) {
///return son[cur][0] == cur || son[cur][1] == cur;
return son[fa[cur]][0] == cur || son[fa[cur]][1] == cur;
}
错误8:
inline void Access(int cur) {
//不是lst = p
for (register int p = cur, lst = 0; p; lst = p, p = fa[p])
splay(p), siz[p] += Siz[son[p][1]], son[p][1] = lst,
siz[p] -= Siz[son[p][1]], pushup(p);
}
错误9:
inline void splay(int cur) {
...
for (register int faa = fa[cur]; notroot(cur); rotate(cur), faa = fa[cur])//rotate(cur)!!!
if (notroot(faa)) rotate(get_which(cur) == get_which(faa) ? faa : cur);
pushup(cur);
}
错误10
inilne void Cut(int x, int y) {
makeroot(x), Access(y);
splay(x);//Attention!!!!!!
son[x][1] = fa[y] = 0;
pushup(x);
}
错误11
inline void Cut(int x, int y) {
make_root(x), Access(y), splay(x);
son[x][1] = fa[y] = 0;
//不要siz[x] -= Siz[y]!!!
pushup(x);
}
错误12
inline void rotate(int cur) {
int faa = fa[cur], fafa = fa[faa];
bool flag = get_which(cur);//not "false"
...
}
错误13
inline void Access(int cur) {
for (register int p = cur, lst = 0; p; lst = p, p = fa[p])
splay(p), son[p][1] = lst, pushup(p);//splay(p)!!
}
模板(主要为make_root,Link,Cut,Split,同模板题,维护链上异或和,除查询外都不保证合法)
inline bool get_which(int cur) {
return son[fa[cur]][1] == cur;
}
inline bool notroot(int cur) {
return son[fa[cur]][0] == cur || son[fa[cur]][1] == cur;
}
inline void pushup(int cur) {
sum[cur] = val[cur] ^ sum[son[cur][0]] ^ sum[son[cur][1]];
}
inline void pushrev(int cur) {
if (!cur) return ;
tag[cur] ^= 1;
swap(son[cur][0], son[cur][1]);
}
inline void pushdown(int cur) {
if (tag[cur])
pushrev(son[cur][0]), pushrev(son[cur][1]), tag[cur] = 0;
}
inline void rotate(int cur) {
int faa = fa[cur], fafa = fa[faa];
bool flag = get_which(cur);
fa[cur] = fafa; if (notroot(faa)) son[fafa][get_which(faa)] = cur;
son[faa][flag] = son[cur][flag ^ 1]; if (son[cur][flag ^ 1]) fa[son[cur][flag ^ 1]] = faa;
son[cur][flag ^ 1] = faa; fa[faa] = cur;
pushup(faa);
}
int stk[N], stop;
inline void splay(int cur) {
int p = cur;
while (notroot(p)) {
stk[++stop] = p;
p = fa[p];
}
stk[++stop] = p;
while (stop)
pushdown(stk[stop--]);
for (register int faa = fa[cur]; notroot(cur); rotate(cur), faa = fa[cur])
if (notroot(faa)) rotate(get_which(faa) == get_which(cur) ? faa : cur);
pushup(cur);
}
inline void Access(int cur) {
int lst = 0;
for (register int p = cur; p; lst = p, p = fa[p])
splay(p), son[p][1] = lst, pushup(p);
}
inline void make_root(int cur) {
Access(cur); splay(cur); pushrev(cur);
}
inline int find_root(int cur) {
Access(cur); splay(cur);
int p = cur;
while (son[p][0]) p = son[p][0];
splay(p);
return p;
}
inline void Split(int x, int y) {
make_root(x); Access(y); splay(y);
}
inline void Link(int x, int y) {
make_root(x);
int rt = find_root(y);
if (x == rt) return ;
fa[x] = y;
}
inline void Cut(int x, int y) {
make_root(x);
int rt = find_root(y);
if (x == rt && fa[y] == x && !son[y][0])
fa[y] = son[x][1] = 0, pushup(x);
}