题目描述
现在有一个圈,圈上有n个点,每个点之间的距离是m,你从起点出发,带着t个跳跃模组进行巡逻,每次使用一次跳跃模组i,跳跃的距离是ai
一个合法的巡逻路线理应从一个点开始,经过若干次跳跃之后(顺时针或者逆时针),在某个点停下来(不一定要用掉所有的跳跃模组)
或者更正式地说∑ai∗xi≡0(mod m), 其中xi可以是±1,0, 但是不能全为0
一个邪恶的破坏者想要让你无法完成合法的跳跃,现在,你想要知道有多少种可能的破坏(也就是拿掉若干个跳跃模组)方案,答案也许很大,请将答案对10^9+7取余
输入格式
第一行输入三个整数n, m, t
第二行t个整数,表示每个跳跃模组的跳跃距离ai
输出格式
输出使你无法进行巡逻的破坏方案总数
样例输入
7 6 5
5 4 12 6 5
样例输出
6
数据规模
对于10%的数据,t≤10
对于30%的数据,m≤70
对于60%的数据,m≤100
对于100%的数据,2≤n≤1000,1≤m≤120,1≤t≤10000,每个跳跃的距离不超过10^9
一道原本坐等有人接单然后听题解结果石沉大海的题目,只好麻烦把学长问到吐血了



其实题目就是 ∑ai∗xi≡0(mod m), 其中xi可以是±1,0, 但是不能全为0,让其不成立,如果我们真的去破坏的话。。。我也不知道怎么做了,暴力吧
所以我们反过来直接枚举对于 “∑ai∗xi≡0(mod m), 其中xi可以是±1,0, 但是不能全为0” 来说非法的情况
由于是∑ai∗xi≡0(mod m),在mod m的意义下,我们将ai做如下处理,ai=min(ai%m,(m-ai)%m),即在顺时针和逆时针走中取一个最小值,为什么呢,因为我们要压ai的范围,经过这么处理以后,ai的范围就在60以内了
然后我们进行拼凑,拿着目前的ai,只要它mod m 不为0,那么都是对答案有贡献的,将手上所有的ai都用上(即为破坏原题目的合法性)。
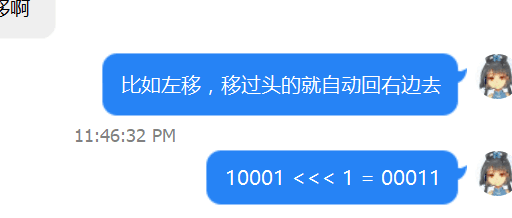
这题ai的范围有60,所以我们直接枚举ai就好了,对于目前的长度x,其对应有一个计数器S,二进制下S的每一位表示此时长度是否已经被凑出来过,用0与1表示,那么对于每个长度,首先只要这个长度是合法的,我们就可以将他们都用上,这有一种贡献,当这个长度是我们处理过的ai时,首先我们先确定它是否合法,即看S中有没有已经凑出过的长度,如果有,那么顺时针一下逆时针一下就不能破坏了,这种就对答案没有贡献了,所以在保证是合法的情况下,我们对于每个原有的长度加上ai或者减去ai,咋办呢?——循环位移,左移移右移移就好了,啊,什么是循环位移
所以这道题就是这样啦。。。
其实代码也不会很长。。。

#include<iostream> #include<cstdlib> #include<cstdio> #include<algorithm> #define ull unsigned long long #define mod 1000000007LL using namespace std; int n,m,t,cnt[71],REV[1<<16]; ull fullnum; inline int fix(int x){ while(x<=0) x+=m; while(x>=m) x-=m; return x; } inline int rev16bit(int x){ int ret=0; for(int i=1;i<=16;i++) ret=2*ret+(x&1),x/=2; return ret; } inline ull reverse(ull x) { ull A = (x>>48) & ((1LL << 16)-1); ull B = (x>>32) & ((1LL << 16)-1); ull C = (x>>16) & ((1LL << 16)-1); ull D = (x) & ((1LL << 16)-1); A = REV[A], B = REV[B], C = REV[C], D = REV[D]; return ((D<<48)|(C<<32)|(B<<16)|A); } inline ull xh(ull curMask, int shift) { ull ret = curMask; ull rev = reverse(curMask) >> (63 - m/2); ret |= (curMask << shift); ret |= (curMask >> shift); ret |= (rev >> (m/2 - shift)); ret |= (rev << (m/2 + (m&1) - shift)); return ret & fullnum; } inline long long dfs(int x,long long S){ if(x>m/2+1) return 1; long long ret=0; ret+=dfs(x+1,S); if(cnt[x]>0) if((S&(1LL<<x))==0) ret+=cnt[x]*dfs(x+1,xh(S,x)); ret=ret%mod; return ret; } inline void Jimmy(){ scanf("%d%d%d",&n,&m,&t); for(int i=0;i<(1<<16);i++) REV[i]=rev16bit(i); fullnum=(1LL<<(1+m/2))-1; for(int i=1;i<=t;i++){ long long c; scanf("%lld",&c); cnt[min(fix(c%m),fix(-(c%m)))]++; } printf("%lld ",dfs(1,1)%mod); } int main(){ Jimmy(); return 0; }
