二叉树遍历

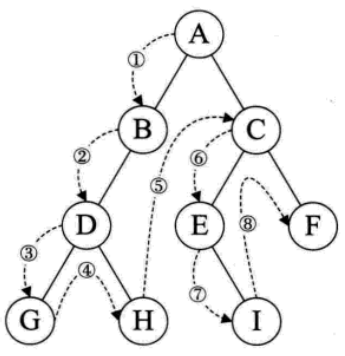
1.前序遍历

个人记忆法：自己、左、右（每个节点都先考虑它自己，再考虑它的左子树，最后考虑它的右子树，首先从二叉树的根节点开始考虑）

1.1递归版

struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x): val(x), left(NULL), right(NULL) { }
};

void preOrderTraverse(TreeNode* node)
{
    if (node == NULL)
        return;
    cout << node->val << endl;    /* 显示结点数据，可以更改为其它对结点操作 */
    preOrderTraverse(node->left); /* 前序遍历左子树 */
    preOrderTraverse(node->right); /* 前序遍历右子树 */
}

1.2非递归版

转载自：https://www.jianshu.com/p/49c8cfd07410

思想：有重合元素的局部有序一定能组成整体有序

void preOrderTraversal(TreeNode* root)
{
    stack<pair<TreeNode*, bool>> sta;
    sta.push(make_pair(root, false));
    bool visited;
    while (!sta.empty())
    {
        TreeNode* node = sta.top().first;
        visited = sta.top().second;
        sta.pop();
        if (node == NULL)
            continue;
        if (visited)
            cout << node->val << endl;
        else  //栈：后进先出
        {
            sta.push(make_pair(node->right, false));
            sta.push(make_pair(node->left, false));
            sta.push(make_pair(node, true));
        }
    }
}

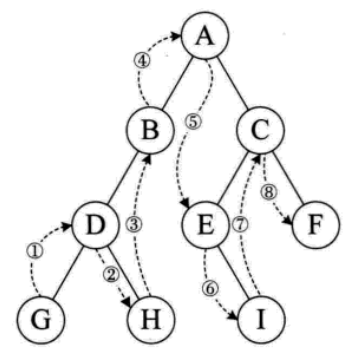
2.中序遍历

个人记忆法：左、自己、右

2.1递归版

void inOrderTraverse(TreeNode* node)
{
    if (node == NULL)
        return;
    inOrderTraverse(node->left); /* 中序遍历左子树 */
    cout << node->val << endl;    /* 显示结点数据，可以更改为其它对结点操作 */
    inOrderTraverse(node->right); /* 最后中序遍历右子树 */
}

2.2非递归版

在前序遍历非递归版的基础上稍微变下即可

void inOrderTraversal(TreeNode* root)
{
    stack<pair<TreeNode*, bool>> sta;
    sta.push(make_pair(root, false));
    bool visited;
    while (!sta.empty())
    {
        TreeNode* node = sta.top().first;
        visited = sta.top().second;
        sta.pop();
        if (node == NULL)
            continue;
        if (visited)
            cout << node->val << endl;
        else  //栈：后进先出
        {
            sta.push(make_pair(node->right, false));
            sta.push(make_pair(node, true));
            sta.push(make_pair(node->left, false));
        }
    }
}

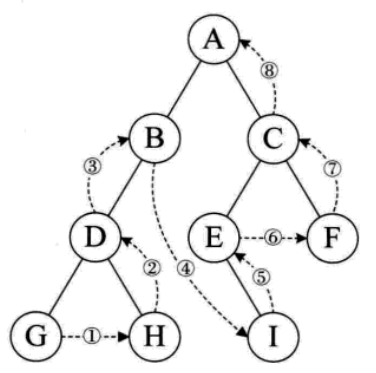
3.后序遍历

个人记忆法：左、右、自己

3.1递归版

void postOrderTraverse(TreeNode* node)
{
    if (node == NULL)
        return;
    postOrderTraverse(node->left); /* 先后序遍历左子树 */
    postOrderTraverse(node->right); /* 再后中序遍历右子树 */
    cout << node->val << endl;    /* 显示结点数据，可以更改为其它对结点操作 */
}

3.2非递归版

在前序遍历非递归版的基础上稍微变下即可

void postOrderTraversal(TreeNode* root)
{
    stack<pair<TreeNode*, bool>> sta;
    sta.push(make_pair(root, false));
    bool visited;
    while (!sta.empty())
    {
        TreeNode* node = sta.top().first;
        visited = sta.top().second;
        sta.pop();
        if (node == NULL)
            continue;
        if (visited)
            cout << node->val << endl;
        else  //栈：后进先出
        {
            sta.push(make_pair(node, true));
            sta.push(make_pair(node->right, false));
            sta.push(make_pair(node->left, false));
        }
    }
}

4.层序遍历

按层从左到右

void floorOrderTraverse(TreeNode* T)
{
    if (T == NULL)
        return;
    queue<TreeNode*> que;
    que.push(T);
    while (!que.empty())
    {
        BiTree* front = que.front();
        cout << front->val << endl;
        que.pop();
        if (front->left)
            que.push(front->left);
        if (front->right)
            que.push(front->right);
    }
}

 4.1变型

单数层从左往右，双数层从右往左

/*不用queue，用vector，打印和存新节点分开进行*/
void newFloorOrderTraverse(TreeNode* root)
{
    if (root == NULL)
        return;
    vector<TreeNode*> vec;
    vec.push_back(root);
    int floor = 1;
    while (!vec.empty())
    {
        if (floor % 2 == 1)
        {
            for (int i = 0; i < vec.size(); ++i)
                cout << vec[i]->val << endl;
        }
        else
        {
            for (int i = vec.size()-1; i >=0 ; --i)
                cout << vec[i]->val << endl;
        }
        vector<TreeNode*> temp;
        for (int i = 0; i < vec.size(); ++i)
        {
            if (vec[i]->left != NULL)
                temp.push_back(vec[i]->left);
            if (vec[i]->right != NULL)
                temp.push_back(vec[i]->right);
        }
        vec.assign(temp.begin(),temp.end());
        ++floor;
    }
}

5.确定一棵二叉树

前序遍历+中序遍历、后序遍历+中序遍历可以确定；

前序遍历+后序遍历不可确定：前序可以确定其第一个元素为根节点，后序可以确定其最后一个元素为根节点，但是无法推断出左右子树，所以GG

6.测试例二叉树构造

    vector<TreeNode*> a;
    for (int i = 0; i < 15; ++i)
        a.push_back(new TreeNode(i + 1));
    a[0]->left = a[1];
    a[0]->right = a[2];

    a[1]->left = a[3];

    a[2]->left = a[4];
    a[2]->right = a[5];

    a[3]->left = a[6];
    a[3]->right = a[7];

    a[4]->left = a[8];

    preOrderTraversal(a[0]);    //前序遍历，可替换成相应遍历
    for (int i = 0; i < 15; ++i)
        delete a[i];

此测试二叉树的打印结果：（图中ABCDEFGHI对应123456789）

　　前序遍历：124783596

　　中序遍历：748215936

　　后序遍历：784295631

　　层序遍历：123456789

　　层序遍历变型：132456987