二叉查找/搜索/排序树 BST (binary search/sort tree)
或者是一棵空树;
或者是具有下列性质的二叉树:
(1)若它的左子树不空,则左子树上所有结点的值均小于它的根节点的值;
(2)若它的右子树上所有结点的值均大于它的根节点的值;
(3)它的左、右子树也分别为二叉排序树。
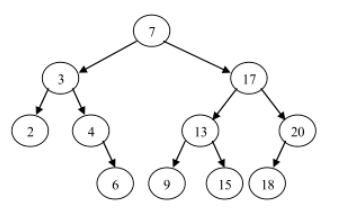
注意:对二叉查找树进行中序遍历,得到有序集合
平衡二叉树(Self-balancing binary search tree) 自平衡二叉查找树 又被称为AVL树(有别于AVL算法)
https://blog.csdn.net/weixin_38075257/article/details/87949296
平衡二叉树:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
1、平衡二叉树又被称为AVL树,或者一颗空树,或者是具备以下特征的一种特殊的二叉查找树:
(1)它的左右两个子树的高度差(平衡因子)的绝对值不超过1;
(2)并且左右两个子树都是一棵平衡二叉树;
2、平衡因子:左子树的高度-右子树的高度
以下图为例,左边每个节点的平衡因子绝对值均不超过1,为平衡二叉树;右边树中存在平衡因子绝对值超过2的节点,不是平衡二叉树
平衡二叉树的目的是为了减少二叉查找树层次,提高查找速度;平衡二叉树可以解决二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O ( l o g N ) O(logN)O(logN)。
3、平衡调节: 当我们往一个平衡二叉树插入一个新的子节点,可能造成平衡二叉树的失衡,即存在有节点的平衡因子为2或者-2的状态,因此我们需要调节二叉树,使之保持平衡。通常会出现四种情况,因此需要四种操作来平衡二叉树。【注意:旋转过程中要注意平衡二叉树是二叉排
序树的特点】
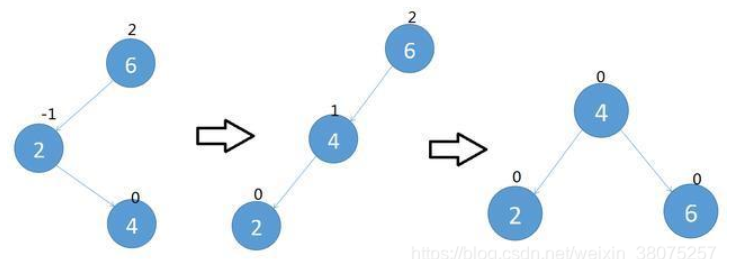
(1) 右旋:当有节点的平衡因子为2时,说明左边子树深度大于右边,因此需要右旋。
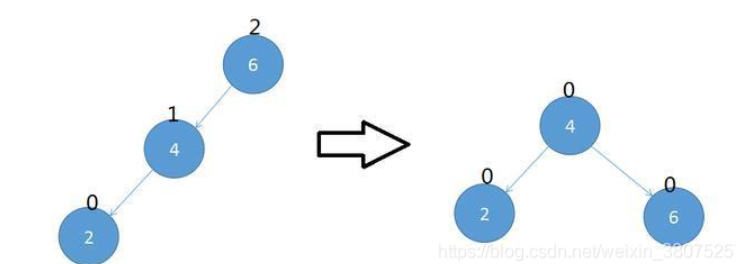
(2) 左旋:当有节点的平衡因子为-2时,说明右边的子树的深度大于左边,因此需要左旋。

(3) 右左旋:先让子树4和6右旋,再整体左旋

(4)左右旋:先让子树2和4左旋,再整体右旋
红黑树R-B Tree
红黑树,是一种平衡二叉树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红或黑。满足:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点是黑色。【注:这里叶子节点,是指为空(NIL或NULL)的叶子节点】
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
【注】:特性(3)中的叶子节点,是只为空(NIL或null)的节点;特性(5)确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对接近平衡的二叉树
