报告内容如下
-
-
【导语】
------ 太晚了,时间也紧,一切尽量从简吧
PS:本文题目来自剑锋OI
所以废话也不多说,进入正题吧,代码直接跟在题目后边儿,主要分析在代码前,次要的就写在代码后面了。
-
-
t1. 算筹【普及组多校联盟14】
时间限制:1S / 空间限制:256MB
【问题描述】
算筹计数法是我国古代著名的计数法。它以算筹(即竹签)来表示数字,而表示某一位上的数字有纵式和横式两种方法。
具体来说,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推。
如果某一位上的数字为 0,则留空该位,但并不影响其他位上数字的摆法。其他数字的纵横摆法如下图:
Kornal 学习了算筹计数法后,按照它用竹签摆出一个数字 n。你能帮他统计摆出的算筹数字中,多少根竹签是横着的,多少根竹签是竖着的吗?例如,摆出纵式的 8 就需要横着的竹签 1 根,竖着的竹签 3 根。
【输入格式】
仅有 1 个正整数,表示摆出的数字 n。
【输出格式】
有 2 个整数,用单个空格隔开,分别表示所用横着的竹签数量和竖着的竹签数量。
【输入样例】
17
【输出样例】
2 2
【样例说明】
先摆个位的数字 7,使用纵式,通过查看图,得出需要横竹签 1 根,竖竹签 2 根。
再摆十位的数字 1,使用横式,通过查看图,得出需要横竹签 1 根。
因此,总共需要横竹签 2 根和竖竹签 2 根。
【数据范围】
对于 25% 的数据,有 n ≤ 10,000。
对于 所有 的数据,有 n ≤ 10^100。
【题目分析】
总体来讲也不是很难,毕竟t1(如果是加点料就称得上是坑题了)。
但在本题中还是有许多要注意的地方的:
- 所谓横纵—–其实微微留点心就会发现其实纵式和横式的摆法就是互相反着来的,比如横式的 8 有横着三根、竖着一根,但纵式的 8 也就是变成了竖着三根、横着一根罢了。然后就只用判断一下横、纵再分情况加就ok啦(不过写两个数组也没关系,就是用一个数组更省码程序的时间吧,况且这省空间也是个习惯问题,所谓细节决定成败嘛)
- n的取值范围—–奔着25分去的的就不用考虑这点了,但问题是这可是t1!不那个满分对得起出题人(苏大佬)吗?然后就看到n的上限贼大,然后就有部分OI选手用了getchar,问题是这样用string不是更简单吗?要知道存个字符也就1字节,100个字符也就100字节,所以用string还更省空间!并且每次用一位就拿着下标取一位(从后往前取),操作更简单。
- no more。开始模拟
【程序代码】
#include<bits/stdc++.h>
using namespace std;
string s; //定义一个string类型的s
int f=1,heng,shu; //f从1开始,不赋初始值也行,下面判断改成f%2==0就好了
struct tmood //结构体存储横式(倒过来就是纵式)数字所用的---
//横着竖着的木条的多少
{
int h,
l;
}a[10]; //从0到9,开10个tmood
void read() //初始化部分,读入数字字符串并给每个数字横、竖所用的木条数赋初始值 (用for循环以木条摆放规律赋值)
{
cin>>s;
for(int i=0;i<=5;++i)
a[i].h=i;
for(int i=6;i<=9;++i)
a[i].h=i-5,a[i].l=1;
}
int main()
{
read();
int len=s.length()-1;
while(len+1)
{
int x=s[len]-'0';
// cout<<x<<endl; //调试的习惯
// cout<<a[x].h<<" "<<a[x].l<<endl;
if(f%2) //判断是不是第奇数位(从后往前数)
{
heng+=a[x].l;
shu+=a[x].h;
}
else //这里用相反的赋值就好了
{
heng+=a[x].h;
shu+=a[x].l;
}
--len; //更新下标
++f; //修改位数
}
printf("%d %d
",heng,shu); //大功告成
return 0;
}-
t2.黑洞【普及组多校联盟14】
时间限制:1S / 空间限制:256MB
【问题描述】
所谓数学黑洞,就是不论取什么数,按照一定的规律不断获得一个新数,最终都会困入一个数循环,就像现实中的黑洞吸引任何物质一样。
角谷猜想就是一个著名的数学黑洞。Kornal 经过研究,也发现了一个数学黑洞,他称之为 K 数字黑洞:对于任何自然数n,每次转换使它减去小于等于它的最大平方数(如 0,1,4,9,16,25……),不断执行该转换,最终必然会困入 0 的循环。
例如,给出一个数 15,因为小于等于 15 的最大平方数是 9,所以得到新数 15-9=6;而对于 6,小于等于 6 的最大平方数是 4,所以得到新数 6-4=2;类似地,可以得到数 1,最后落入 0 的循环。
由此可见,数字 15 在 K 数字黑洞 的规则下,不断取了 6,2,1,0 这些新数,现在定义自然数的 K 集合的元素为这个自然数自身,以及在 K 数字黑洞 规则下不断取的新数,即数字 15 的 K 集合是 {15,6,2,1,0}。
那么现在问题来了:给定正整数 l 和 r,求大于等于 l 小于等于 r 的所有自然数中,其 K 集合中拥有元素 l 的自然数数量。
(赛后思考题:给定正整数 m,找出规律,得到最小的自然数,使其K 集合中有 m 个元素。)
【输入格式】
第 1 行,有 2 个正整数,分别表示 l 和 r。
【输出格式】
仅 1 个整数,表示大于等于 l 小于等于 r 的所有自然数中,K 集合拥有元素 l 的自然数数量
【输入样例】
2 6
【输出样例】
3
【样例解释】
大于等于 2 小于等于 6 的正整数有 2,3,4,5,6。
数字 2 在 K 数字黑洞下,K 集合为 {2 ,1 ,0}。其中有元素 2,所以统计入答案。
数字 3 在 K 数字黑洞下,K 集合为 {3 ,2 ,1 ,0}。其中有元素 2,所以统计入答案。
数字 4 在 K 数字黑洞下,K 集合为 {4 ,0}。其中没有元素 2,所以不统计入答案。
数字 5 在 K 数字黑洞下,K 集合为 {5 ,1 ,0},。其中没有元素 2,所以不统计入答案。
数字 6 在 K 数字黑洞下,K 集合为 {6 ,2 ,1 ,0}。其中有元素 2,所以统计入答案。
综上所述,答案即为 3。
【数据范围】
对于 70% 的数据,有 1 ≤ l ≤ r ≤ 1,000,000。
对于 所有 的数据,有 1 ≤ l ≤ r ≤ 30,000,000。
【题目分析】
首先出题人(Mr Su)是用dp(动态规划)做的,是非常的简洁明了,那么鄙人不才,又是用了个深搜(记忆化搜索),相较于dp的程序比较长,不过效果还好的样子,这里就分享一下咯
那么记搜总体思路还是从后往前枚举的,而dp就是从前往后做的了,具体还是看代码吧
【程序代码】
#include<bits/stdc++.h> //sqrt()
using namespace std;
int l,r,s,ans;
int vis[30000005];
int dfs(int n)
{
if(n<l) return 1; //都查到比l小的数了,集合中当然没有l,返回1
if(n==l) return 2; //找到了返回2
int f=sqrt(n); //开根号自动向下取整
if(vis[n-f*f]) return vis[n]=vis[n-f*f];//如果搜过了就直接返回
return vis[n]=vis[n-f*f]=dfs(n-f*f);//不然就往下搜
//注意:以上两个return中都含有赋值语句,这就是记忆化在起作用了,不会让搜索重复,但会消耗vis[]这个数组的空间,所以有利有弊,但是本题中还是利大于弊
}
int main()
{
//freopen("000.in","r",stdin); //无聊写的,方便读入
//freopen("000.out","w",stdout);//无聊写的.方便查看用时(就是怕TLE)
cin>>l>>r;
while(r>0) //注意是大于0,“>0”不写也没事
{
if(dfs(r)==2) //以2为查找成功,1为查找失败
ans++; //答案加一
--r; //往前枚举
}
cout<<ans<<endl;
return 0;
}好了下一题!额…不对,再附上出题人的dp代码吧!(笔记是出题人做的)
#include <iostream>
#include <cmath>
using namespace std;
int l , r , tmp , ans;
bool f[30000001]; // f[i] 表示 i 的 K 集合中是否有元素 l
int main(){
cin >> l >> r;
f[l] = true , ans = 1;
// l 的 K 集合中一定有元素 l,所以 f[l] = true 且答案初始化为 1
for(register int i = l + 1 ; i <= r ; i++){
// 使用 register 可以勉强加一些速度
tmp = floor(sqrt(i)); tmp = i - tmp * tmp;
// 先求出 i 的第一次会转换成什么数,存储在变量 tmp 中
if(f[tmp])
f[i] = true , ans++;
// 如果 tmp 的 K 集合中有元素 l,既然 i 将会转换成它
// 那么 i 的 K 集合中必然也有元素 l,统计入答案
}
cout << ans << endl;
return 0;
}-
t3.冒泡【普及组多校联盟14】
时间限制:1S / 空间限制:256MB
【问题描述】
水池上冒出了 n 个大小相同的泡泡,Kornal 看到后想让它们立马消失。
泡泡的位置恰好可以在平面直角坐标系上用坐标表示,每个泡泡都可以看成一个点,并互不重合。
Kornal 可以主动戳破泡泡,如果任何一个泡泡被破坏,它溅出的水花会击破和它同一横坐标或同一纵坐标的其他泡泡,而那些被水花破坏的泡泡自身也会溅出水花,直到没有泡泡能被水花破坏为止,此时 Kornal 才能再去戳“幸存”的泡泡,这一系列的破坏是瞬间的。当然,泡泡被破坏了就不会再次出现。
那么要让所有的泡泡都消失,Kornal 最少要戳多少下?在此条件下,戳破一个泡泡,瞬间最多能有多少个泡泡被破坏呢?
如下图,为水池上的 5 个泡泡,如果 Kornal 主动戳破泡泡 1,则其溅出的水花会击破泡泡 3,而泡泡 3 的水花又会击破泡泡 5,瞬间就有 3 个泡泡被破坏。
接下来,Kornal 再戳破泡泡 2,泡泡 2 的水花会将泡泡 4 击破,只瞬间破坏了 2 个泡泡。
因此,想让所有泡泡都消失,Kornal 最少要戳破 2 个泡泡,其中最多瞬间有 3 个泡泡被破坏。
Markdown
【输入格式】
第 1 行,有 1 个正整数,为泡泡的数量 n。
接下来有 n 行,每行有 2 个整数,分别表示第 i 个泡泡的坐标 (x[i] , y[i])。
【输出格式】
有 2 个整数,用单个空格隔开,分别表示破坏所有泡泡要戳的最少次数和瞬间破坏的泡泡最多的数量。
【输入样例】
5
2 4
1 3
2 1
3 3
4 1
【输出样例】
2 3
【数据范围】
对于 50% 的数据,有 n ≤ 1,000,0 < x[i] ≤ 1,000,0 < y[i] ≤ 1,000。
对于 所有 的数据,有 n ≤ 100,000,-10^7 ≤ x[i] ≤ 10^7,-10^7 ≤ y[i] ≤ 10^7。
【题目分析】
看到冒泡是不是很激动?你以为?ACM题?作者大大没这么好心t3还送分,但是还是要弱弱的吐槽一句:题目与内容不符 啊!!!
然后又是用了深搜,拿了个65,爆了7个点,都是TLE :(
所以深搜还是谨慎用吧,本题正确思路是并查集(出题者大大的思路),那么本来我的思路是用二维数组骗个50分也差不多了,然后和him磨了个十来分钟,还是写了个深搜,拿了个65,然后65分的代码跟上!
【程序代码】
#include<bits/stdc++.h> //贼长,然后还没满分
#define M 100005
using namespace std;
int n,lef,tim,maxx; //n表示有多少个泡泡(一直都不改变)
//lef表示剩下多少个泡泡(初始值为n)
//tim表示一共扎了几次(while循环里一直++统计)
//maxx表示一次最多爆多少个泡泡
bool used[M]; //used[i]记录着第i个点报了没有,0表示没有,1表示爆了
struct tp //记录每个泡泡的坐标
{
int x,
y;
}a[M];
int read() //读入优化,不过看到结果之后心都寒了(第13个点才256ms第14个点就爆了,然后后面都爆了...),这优化了也没啥用的样子哦...(本题中)
{
char c=getchar();
int x=0,f=1;
while(!isdigit(c) && c!='-') c=getchar();
if(c=='-')
{
f=-1;
c=getchar();
}
while(isdigit(c))
{
x=(x<<1)+(x<<3)+c-'0';
c=getchar();
}
return x*f;
}
int pop(int j) //深搜部分
{
int many=1; //要把自己这个泡泡(即将爆掉的)统计进去吧。
used[j]=1; //然后used[j]变为1表示已经爆掉了
lef--; //存活着的泡泡-1
for(int i=1;i<=n;++i)//遍历每个泡泡,与当前泡泡在同行或同列的没爆掉的泡泡都炸爆,然后以这些爆掉的泡泡再深搜并返回值加给many,统计总共扎爆几个
{
if(used[i])
continue;
if(a[i].x==a[j].x || a[i].y==a[j].y)
many+=pop(i);
}
return many; //返回many(本次炸爆的泡泡数)
}
int main()
{
/* 读入部分 */
n=read();
lef=n;
for(int i=1;i<=n;++i)
{
a[i].x=read();
a[i].y=read();
}
/*****************/
while(lef) //看看有没有泡泡剩下来的
{
tim++; //扎泡泡的次数++
int num=1;
while(used[num]) num++; //把扎过的泡泡都跳过去
maxx=max(maxx,pop(num)); //用深搜的返回值比较得出--
//每次扎泡泡最多消灭的泡泡数
}
printf("%d %d
",tim,maxx);
return 0;
}那么深搜完毕了,65分有了,满分怎么办呢?就用并查集啊!所谓并查集就是把几个集合归为一类(一般是有所联系的集合),然后大集合中的每个点都指向一个点(不确定的点但一定在集内),总之更多就查百度百科或者上CSDN啦!
附上一个关于并查集的网页:
!!!并查集!!!<<点这里
话不多说,上并查集!(注释为出题人所写)
#include <cstdio>
#include <algorithm>
using namespace std;
struct Point{
int x , y , n;
// 泡泡结构体,x 横坐标,y 纵坐标,n 原始编号
};
bool CmpX(Point x , Point y){
// 排序的比较函数,以泡泡的横坐标为关键字
return x.x < y.x;
}
bool CmpY(Point x , Point y){
// 排序的比较函数,以泡泡的纵坐标为关键字
return x.y < y.y;
}
Point P[100001];
int n , ans = 0 , _max , c[100001] , f[100001];
int Find(int d){
// 并查集的寻找祖先函数
return f[d] == d ? d : f[d] = Find(f[d]);
}
int main(){
scanf("%d" , &n);
for(int i = 1 ; i <= n ; i++)
scanf("%d%d" , &P[i].x , &P[i].y),
P[i].n = i , f[i] = i; // 初始化编号和祖先
sort(P + 1 , P + n + 1 , CmpX);
// 先按横坐标排序,便于将相同横坐标的泡泡合并
for(int i = 2 ; i <= n ; i++)
if(P[i - 1].x == P[i].x)
f[Find(P[i].n)] = Find(P[i - 1].n);
// 如果两个泡泡横坐标相同,按原始编号合并
sort(P + 1 , P + n + 1 , CmpY);
// 再按纵坐标排序,便于将相同纵坐标的泡泡合并
for(int i = 2 ; i <= n ; i++)
if(P[i - 1].y == P[i].y)
f[Find(P[i].n)] = Find(P[i - 1].n);
// 如果两个泡泡纵坐标相同,按原始编号合并
for(int i = 1 ; i <= n ; i++)
c[Find(i)]++; // 给自己的终极祖先加一,便于统计最大瞬间破坏数
for(int i = 1 ; i <= n ; i++)
if(f[i] == i){ // 如果终极祖先是自己,执行操作
ans++;
if(_max < c[i])
_max = c[i]; // 更新最大瞬间破坏数
}
printf("%d %d
" , ans , _max);
return 0;
}t4. 框数【普及组多校联盟14】
时间限制:1S / 空间限制:256MB
【问题描述】
Kornal 随手画了一个 n × n 的整数方阵,并在这个矩阵中开始了框数游戏。规定:他每画一个方框,大小为 s,可获得所框住的 s × s 个数总和的分数。
Kornal 的初始分数为 0。首先他画了一个 n × n 的方框,框住了方阵内的所有数,因此可以获得所有数之和的分数。接下来,他需要不断在上一次所画的方框内部,画一个大小比上一次小 1 的方框,并对应获得分数,直到画了大小为 1 的方框,只能框 1 个数为止。
给出 Kornal 的方阵,你能求出 Kornal 的框数游戏最多能获得多少总分吗?
【输入格式】
第 1 行,有 1 个正整数,表示方阵的大小 n。
接下来 n 行,每行有 n 个整数,表示方阵每行每列的数字,第 i 行第 j 列的数字是a[i][j]。
【输出格式】
仅 1 个整数,有框数游戏最多能获得的总分。
【输入样例】
3
1 1 1
1 3 2
1 2 2
【输出样例】
26
【样例说明】
在该方阵上进行框数游戏,获得的最大总分为 26,框数流程如下:
第 1 次框数,框住整个方阵,获得分数 1 × 5 + 2 × 3 + 3 = 14。
第 2 次框数,框住 3,2,2,2,获得分数 2 × 3 + 3 = 9。
第 3 次框数,框住 3,获得分数 3。
因此这 3 次框数总共获得分数 14 + 9 + 3 = 26。
【数据范围】
对于 20% 的数据,有 n ≤ 8,1 ≤ a[i][j] ≤ 100。
对于 50% 的数据,有 n ≤ 15,-1,000 ≤ a[i][j] ≤ 1,000。
对于 所有 的数据,有 n ≤ 100,-1,000,000 ≤ a[i][j] ≤ 1,000,000。
【题目分析】
本来想偷偷懒套一下出题人的分析报告的,然后发现图片弄来弄去太麻烦索性就算了。
那么出题人的思路呢就是dp(真是一言不合就dp,我还是继续一言不合就深搜吧)。不过前缀和是dp和深搜都要用到的,表示的方法嘛。。。就看程序吧
这里列一下注意事项:
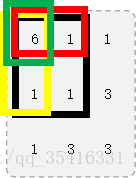
前缀和:表示方法如程序所示,如何求如图所示的框内的数?相信大家听过一维数组的前缀和的表示方法,那么出题人(Sooke先森)别出心裁,设计了个矩阵前缀和来坑大家,那么对此我的方法还是找规律啦。首先假定一下在(i,j)之前的矩阵前缀和都已经求好了(如图则是i=2,j=2),那么如何表示(i,j)这一位置的矩阵前缀和呢?如图可知,黑框内数字的值(即(i,j)这一位置的矩阵前缀和)可以由红色框内的数字加上黄色框内的数字然后再减去绿色框内的数字然后再加上 f 数组里存着的(i,j)本身坐标的值得到,看不懂?没事儿,多看几遍就懂啦!由此可得推导公式(a数组用来存储前缀和数据):a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+f[i][j](程序中直接用读入代替);
然后再想一想,第一行的前缀和和第一列的前缀和也可以用这个推导公式(有第0行、第0列顶着嘛),所以就没问题了!不信就自己试试。然后还要注意数组得从(1,1)存到(n,n),不能从(0,0)开始,不然会RE(runtime error),因为第0行0列前面就是-1行-1列了,没有这样的下标,所以会出错。
然后说一下出题人的注意事项
- 贪心算法是错的:贪心算法好是好,但贪心算法很大的一个限制性就是不能有后效性,而本题在框了一个矩阵之后还要继续框,也就是说如果总数值更大的矩阵被贪心的时候割掉了(不要的那块),那么会对答案产生影响。哎,算了,还是附上出题人的两张图你自己模拟一下吧。。。 -
总之就是如图所示手算一下就知道贪心是错的了
.
.
.
.
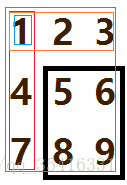
- 还有一点就是关于我的深搜啊,是从大到小框的(而dp是从小到大框的)但是框住的那块内容可能是在中间啊!所以呢,这里是要讲一下表示方法的:(偷张图呵呵)如下,黑框内就是要加起来的数,怎么算?绿的加减去红的减去橙的加上蓝的,这里不做太多解释因为时间不够了 -(:」∠)_ 然后用f[lon][i][j](lon表示大小,i表示上界限,j表示左界限)表示可得公式:f[lon][i][j]=a[i+lon][j+lon]-a[i][j-1]-a[i-1][j]+a[i-1][j-1].别问我为什么多看几遍就知道了。
- 然后最后一点就是变量的类型了:不是int 而是 long long!否则30分就去了。为什么捏?就拿极端数据来说好了100*100*10000000就是10的11次了,超过了10的7次了吧!所以捏,这个坑还是有点坑的。毕竟30呢!
然后就是程序了:
*
*
*
【程序代码】
#include<bits/stdc++.h>
#define M 105
using namespace std;
long long n,a[M][M];
long long maxx[M][M][M]; //上下左右边界值
int h[4]={0,0,1,1},l[4]={0,1,0,1};
int read()
{
char c=getchar();
int x=0,f=1;
while(!isdigit(c) && c!='-') c=getchar();
if(c=='-')
{
f=-1;
c=getchar();
}
while(isdigit(c))
{
x=(x<<1)+(x<<3)+c-'0';
c=getchar();
}
return x*f;
}
long long work(int lon,int up,int lef)
{
if(maxx[lon][up][lef])
return maxx[lon][up][lef];
maxx[lon][up][lef]=a[up+lon][lef+lon]-a[up-1][lef+lon]-a[up+lon][lef-1]+a[up-1][lef-1]; //原本框着的矩阵的总值
long long most=-0x3f3f3f3f; //一开始附很小的值
if(lon==0) most=0; //这里注意lon==0的时候才是大小为一的矩阵特判!
for(int i=0;lon>0 && i<4;++i)//四个方向:左上、左下、右上、右下
{
int xx=up+h[i],yy=lef+l[i];
most=max(most,work(lon-1,xx,yy)); //取四个方向深搜最大值
}
maxx[lon][up][lef]+=most; //加上内部四个方向深搜后的最大值
return maxx[lon][up][lef];
}
int main()
{
n=read();
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
a[i][j]=read()+a[i][j-1]+a[i-1][j]-a[i-1][j-1];
// for(int i=1;i<=n;++i) //小小的调试习惯,可用来查看输出
// {
// for(int j=1;j<=n;++j)
// cout<<a[i][j]<<" ";
// cout<<endl;
// }
printf("%lld
",work(n-1,1,1));
//直接上输出。这里n(框的最大长度)是要-1的,因为下边界值为n,所以:
//下边界值n=n-1(长度-1) + 1(上边界值)
//故n要-1
return 0;
}OK,深搜到此结束,最后附上出t人的dp代码(注释都是原注释 (* /ω\*) ):
#include <cstdio>
#define Max(x , y) ((x) > (y) ? (x) : (y))
int n;
long long a[101][101] , f[101][101][101]; // 用 long long 存
// f[i][j][k] 表示大小为 i 的框的左上角在矩阵 (j , k) 处
// 并且该框里面还分别有 1 ~ i-1 的框,可获得的最大分值
int main(){
scanf("%d" , &n);
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= n ; j++)
scanf("%lld" , &a[i][j]) , f[1][i][j] = a[i][j];
// 输入的同时初始化各个大小为 1 的框住的数字和(其实也就一个数字直接赋值)
for(int i = 1 ; i <= n ; i++)
for(int j = 2 ; j <= n ; j++)
a[i][j] += a[i][j - 1];
// 每行做一次前缀和
for(int j = 1 ; j <= n ; j++)
for(int i = 2 ; i <= n ; i++)
a[i][j] += a[i - 1][j];
// 在每行做了前缀和的基础上做列上的前缀和,这样 a[i][j] 就表示了长 1 ~ i 宽 1 ~ j 的矩形的数字和
for(int s = 2 ; s <= n ; s++) // 枚举下一个框的大小
for(int i = 1 ; i + s - 1 <= n ; i++)
for(int j = 1 ; j + s - 1 <= n ; j++){
// 枚举框的位置,接下来进行转移,可以由四个状态转移来
f[s][i][j] = f[s - 1][i][j];
// 第一种状态,直接赋,更小的框在左上角
f[s][i][j] = Max(f[s][i][j] , f[s - 1][i + 1][j]);
// 第二种状态,更新最大值,更小的框在左下角
f[s][i][j] = Max(f[s][i][j] , f[s - 1][i][j + 1]);
// 第三种状态,更新最大值,更小的框在右上角
f[s][i][j] = Max(f[s][i][j] , f[s - 1][i + 1][j + 1]);
// 第四种状态,更新最大值,更小的框在右下角
f[s][i][j] += a[i + s - 1][j + s - 1] - a[i + s - 1][j - 1] - a[i - 1][j + s - 1] + a[i - 1][j - 1];
// 最后,不要忘记加上自己大小为 s 的框框住的数可获得的分数,可用刚才的前缀和加容斥原理实现
// 不知道这里的原理的可以画画图,首先弄明白 a[i][j] 包含的是什么区域,要求的是什么区域
}
printf("%lld
" , f[n][1][1]);
return 0;
}好了,本次分析报告到此结束,感谢阅读本blog!
〈(_ _)〉 鞠躬 <( ̄︶ ̄)>
顺便推荐一下一个讲SPFA的blog: