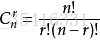关于一些逆元知识的拓展
刚艹完一道 提高- 的黄题(曹冲养猪) ,于是又来混一波讲解了
——承接上文扫盲篇
四、Lucas定理(求大组合数取模)
题外话
这里Lucas定理的证明需要用到很多关于组合数的定理知识,
那么关于一些组合数的知识,详情你可以看这里:Binamoto' blog。
再讲讲lucas定理这个东西(扩展lucas就不讲了,因为不大会…咳咳,然后也不怎么会用到吧)
基本公式: C(n,m) ≡ C(n/p,m/p)*C(n%p,m%p) (mod p)
(也就是: C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p )
适用范围:n 和 m 非常大,而模数 p 比较小的情况 (偷懒)
Lucas 定理的运用
将组合数中的 n 和 m 不断除以 p , 同时用除 p 的余数做组合数,累计入答案。
即,不断调用基本公式,递归求解,直至 m 等于 0 .
用上述例子就是:令C(n/p,m/p) ≡ C( (n/p)/p,(m/p)/p ) * C( (n/p)%p,(m/p)%p ) (mod p)
然后把 C(n/p,m/p) 求得的解 带入基本公式, 求出 C(n,m)%p 的值
证明及推导:
以下证明推导源自 Lucas定理——推导及证明
要证:C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
即证:C(n,m)=C(n/p,m/p)*C(n%p,m%p)
证明条件:已知p是素数,n、m、p为整数。
1.由二项式定理得: 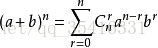
2.由费马小定理得:
(1)式 :$(x + 1) ^p ≡ x+1 (mod~ p)$ **[ 由x ^p ≡ x (mod p) , x 用 (x+1) 代替得到]**
(2)式 :$x ^p + 1 ≡ x+1 (mod~ p)$ **[ 由x ^p ≡ x (mod p) , 等式两边同时+1得到]**
合并 1 、2 两式,得到:
(3)式 :$(x + 1) ^p ≡ x ^p + 1 (mod~ p)$
3.由 $n = n/p *p + n\%p$ . 则:
$(x+1) ^p ≡ (x+1) ^{n/p *p} * (x+1)^{n\%p} (mod p)$
带入三式: $(x+1)^p ≡ (x^p +1)^{n/p}*(x+1)^{n\%p} (mod p)$
将上式由二项式公式可转化为:
$$sum_{z=0}^n C_n^z ·x^z ≡ sum_{i=0}^{n/p} C_{n/p}^i ~·~x^{p ~·~i} sum_{j=0}^{n\%p} C_{n\%p}^j ·x^j Big(mod ~~p Big)$$
任意一个Z,必存在一个 i , j 满足:x ^ z = x ^ (p* i) * x^ j (即满足:n = n/p *p + n%p),
当且仅当: i=z/p,j=z%p 时成立
此时, C(n,m)=C(n/p,m/p)*C(n%p,m%p) 成立
证毕
相信这些东西你在看完后任然是懵逼的(me too)
那么你可以看看另外一个证明(来自可爱的 Binamoto ):
设 $n=s*p+q,m=t*p+r(q,r<=p)$
我们要证 $C_{t*p+r}^{s*p+q} ≡C_{t}^{s} * C_{r}^{q} (modp)$
首先得有个前置知识,费马小定理 $x^p ≡ x (mod p)$
那么 $(x+1)^p ≡ x+1(mod p)$
且 $x^p+1 ≡ x+1 (mod p)$
所以 $(x+1)^p ≡ x^p+1 (mod p)$
然后 $(x+1)^n≡(x+1)^{s*p+q}$
$ ≡ ((x+1)^p)^{s} * (x+1)^q$
$ ≡ (x^p+1)^s * (x+1)^q ≡ (x^p+1)^s * (x+1)^q$
然后用二项式定理展开
≡$sum_{i=0}^{s}C_{s}^{i}*x^{i*p} * sum_{j=0}^{1}C_{q}^{j}*x^{j}$
总之就是 $(x+1)^p ≡ sum_{i=0}^{s} C_{s}^{i} * x^{i*p} *sum_{j=0}^{q} C_{q}^{j}*x^j$
然后考虑把两边的多项式展开一下
那么两边肯定都有 $x^{m}$ 即 $x^{t*p+r}$ 这一项(这是最上面的假设)
左边的 $x^m$ 的系数,根据上面的性质4推出来,应该是 $C_{n}^{m}$
然后右边嘞?只有 $i=t$ , $j=r$ 的时候才会有这一项,所以这一项的系数就是 $C_s^t * C_q^r$
然后又因为 $s=n/p$,$t=n%p$,$q=m/p$,$r=m%p$
然后就能证明: $$C(n,m) ≡ C(n/p,m/p) * C{n%p,m%p} (mod p)$$
然而万一 $q<r$ 该怎么办?那样的话 $j$ 根本不可能等于 $r$ 啊?
所以那样的话答案就是 $0$
因为上面乘上 $C{n%p,m%p}$ 答案就是 $0$
如何证明?
我们设 $f=n-m=z*q+x$
因为 $r>t$ , $x+r ≡ t (mod p)$
所以 $x+r=p+t$
又因为 $z*p+x+q*p+r = s*p+t$
所以 $z+q=s-1$
那么带进通项公式 $C_{n}^{m}= dfrac{n!}{m! * f!}$ 之后,分子中有 $s$ 个 $p$ ,分母中有 $s-1$ 个 {p} ,
抵消之后分子中还有一个 $p$ ,那么这个数就是 $p$ 的倍数, $p$ 必然余 $0$.
Lucas 的代码(同上随意手打):
//by Judge define ll long long ll mod; inline ll quick_pow(ll x,ll p){ ll ans=1; while(p){ if(p&1) ans=ans*x%p; x=x*x%p, b>>=1; } return ans; } inline ll C(ll n,ll m){ ll cn=1,cm=1,res=1; if(n<m) return 0; if(n==m) return 1; if(m>n-m) m=n-m; for(ll i=0;i<m;++i){ cn=(cn*(n-i))%mod; cm=(cm*(m-i))%mod; } res=(cn*quick_pow(cm,mod-2))%mod; //除法转换求逆元 return res; } ll Lucas(ll n,ll m){ ll ans=1; while(n && m && ans){ ans=(ans*C(n%mod,m%mod))%mod; //拆分+递归 n/=mod, m/=mod; } return ans; }
关于 Ex Lucas
这玩意儿别学了,要先会 CRT (可能是 exCRT?)的。
五、解线性同余方程组
其实这个玩意儿没什么高大上的,就CRT ... 什么的,你是没看过 NOI day2 T1 吧,那个玩意儿...不说了,勾起了一些不美好的回忆(据说该题是所有题里面最简单的)
emmmm,首先解释一下这个东西。
线性同余方程组:
( 求解 X ,其中 X 满足以下条件 )
X≡b1 (mod a1)
X≡b2 (mod a2)
...
X≡bn (mod an)
对,就和上面一样,是 n 个式子,(一般)让你求出 X 的最小正整数解(即满足 n 个式子的限制条件),这里看不大懂的话你可以看看曹冲养猪这道题,那个比喻也是蛮生动的
那么这玩意儿怎么解呢? 别急,我们得先来看看 X 有解的条件。
其实条件很简单: b2 - b1 ≡ 0 ( mod gcd(a1,a2) )
证明及推导:
设 X = a1 * x + b1 , 则 a1 * x + b1 ≡ b2 (mod a2) (就是在式 2 中把 X 替换掉)
=> a1 * x ≡ b2 - b1 (mod a2) => a1 * x + a2 * y = b2 - b1
那么和逆元有解条件的证明类似,只有 (b2-b1) | gcd(a1,a2) 时,原式有解(其中 (a) | (b) 代表 a 能被 b 整除 )
证毕
所以呢?证明完了之后有什么用处么? 当然有。
你看啊,上面的那个式子我们推着推着就退出来了一个方程对吧?是不是有点眼熟? (提示一下 ax + by )
emmmm 对吧。就是类似一个扩欧的式子啊,因为 a1 和 a2 已知了啊。
然后我们用扩欧求出 a1*x + a2*y = gcd(a1,a2) 中 y1 的解就离胜利不远了
然后你看看我们解出来的这个 x 和 y ,其实它并不是 a1 * x + a2 * y = b2 - b1 的解(这不显然嘛)
但是! b2 - b1 是可以整除 gcd(a1,a2) 的(否则就是无解的情况),所以我们只需要让 x 和 y 乘以 (b2-b1)/gcd(a1,a2) 就可以令等式成立了
然后我们把 x 带入 X = a1 * x + b1 不就可以得到答案了?
同余方程的合并:
但是这里有个关键问题对吧(上面的这些推导只求出了 两个式子的解啊,我们不是要求满足n 个式子的解吗?)
所以我们要考虑的就是把这个方法延续下去...也就是说我们要把 1、2 两个式子合并起来,与第 3 个式子继续进行以上操作。
怎么合并? => X=X' (mod lcm(a1,a2)) (其中 X' 是由前两个式子得到的答案,这里我们就是让 bi = X' , ai = lcm(a1,a2) )
为什么可以这样合并? 你只要知道 X' 是原式在 lcm(a1,a2) 范围内唯一的解就好了
(大家感性理解一下就好,我也不知道怎么证,已经颓废到懒得想了)
咳咳...简单解释一下:
你应该是知道在 a1 * x + a2 * y = b2 - b1 这个等式中的 x 和 y 的解释不止一种的(这个不知道我也没办法)
我们要改变着个解 就是 让 x 加上(减去) a2/d ,然后让 y 减去(加上) a1/d ,等式依旧成立。(这里 d 表示 gcd(a1,a2) ,下同 )
也就是说我们要用到的 x 可以加上或减去任意个 a2/d ,然后你看一下 : X = a1 * x + b1 ,
也就是说我们每次让 x 变化 ± a2 之后,X 的值就会加上或减去 a1 * a2/d (即 X 可以加上任意个 lcm(a1,a2) ),
由此我们可以很容易看出: X 在 lcm(a1 , a2) 范围内的解是唯一的。
所以两个式子就可以那样合并了...
还看不懂?woc 之前都白推了?emmm ,好吧,让我们看看之前的结论(过程结论):
我们可以让 X 的值加上任意个 lcm(a1,a2)
什么意思? mod lcm(a1,a2) = X 的意思啊!就是说任意一个数只要能 mod lcm(a1,a2) = X
所以这不就和之前那一堆式子 : X ≡ bi (mod ai) 一样了? 推导完毕!
......
那么之后我们就反复迭代以上步骤,得到最终的答案
然后呢...没然后了啊,然后就是代码部分了啊QAQ
代码:
int ex_gcd(int a,int b,int& x,int& y){ //本来不想附 ex_gcd 代码来着的... if(!b) { x=1,y=0;return a; } int d=ex_gcd(b,a%b,y,x); y-=a/b*x; return d; } inline ll solv(int n){ ll x=0,m=1; // x 记录前两个方程组的答案,初始为 0, m 记录前面所有的 a 的 lcm for(int i=1;i<=n;++i){ scanf("%lld%lld",&A,&B); ll b=B-x,d=ex_gcd(m,A,z,y); if (b%d!=0) return -1ll; ll t=b/d*z%(A/d); x+=m*t,m*=A/d; } return x>0?x:x+m; }
关于exCRT
这东西别学了,烦的要命...
六、BSGS 定理 baby-step giant-step
BSGS的用处:
BSGS,魔鬼的步伐,怎么说呢...
有关BSGS的题目大多就是让你求 满足 $a^n ≡ 1 (mod p)$ 的最小的 n ,p 为质数
注意 p 为质数!否则就是 exBSGS
注意 n 是最小的,然后我们求出的 n 就是 a 模 p 意义下的阶
题外话:
这个东西很重要,为什么?因为 NTT 里面有用到原根...
原根是什么东西?原根就是:
对于一个数 a ,若其满足 a 在模 p 意义下的阶等于 p 的 φ 值(就是欧拉函数值),则 a 为 p 的阶
那么当 p 为质数时, φ 就为 p-1 咯。
小插曲:你知道大质数 998244353 怎么来的么?(不要告诉我你不知道这个模数)
其实它是从 NTT 中出来的,因为它的一个原根是 3 ,比较好记
另外,$998244353=7 * 17 * 2^23 + 1$
BSGS是什么:
讲了这么多没用的。。。我们回到原来的问题
原本的问题是: 让你求 满足 $a^n ≡ 1 (mod p)$ 的最小的 n
那么我们考虑分块,我们令 $a^n=a^{gt} imes a^h (mod p)$
其中 $t = sqrt{p}$, g 、h 是未知数
那么 h 肯定是小于 t 的对吧?不然的话只要让 g 加上一,h就可以减去 t, 然后等式仍然成立
那么我们先考虑 g 的最大值是多少:
我们看看,a^p-1 是多少? 明显是 1 吧? 根据费马小定理来的,不证了
那么也就是说 p-1 是一个 a 的循环节,那么 g 的最大值就是 $sqrt{p}$ 了
然后考虑一下我们只需要$O(sqrt{p})$去枚举 g ,然后算出值存进map(或者hash表,更快)
然后原问题就可以转换为求找出是否存在 h ($h<=sqrt{p}$) 使得 $a^{gt} imes a^h ≡ 1(mod p)$
然后移一下项就可以变成 $a^{gt} ≡ a^{-h}(mod p)$ ,其中 $a^{-h}$就是 $a^h$ 的逆元
然后再$O(sqrt{p})$枚举 h ,算出 $a^{-h}(mod p)$ 然后看看 map 中有没有这个数,有的话 g*t+h 就是原等式的一个解了
其实不难吧?分块暴力嘛
(poj)
1 inline void insert(int x,int y){ int k=x%mod; 2 hs[++pat]=x,id[pat]=y,nxt[pat]=head[k],head[k]=pat; 3 } 4 inline int find(int x){ int k=x%mod; 5 for(int i=head[k];i>=0;i=nxt[i]) 6 if(hs[i]==x) return id[i]; return -1; 7 } 8 inline int BSGS(int a,int b,int n){ 9 memset(head,-1,sizeof(head)); 10 pat=0; if(b==1) return 0; 11 int m=sqrt(n+0.0),j; ll x=1,p=1; 12 for(int i=0;i<m;++i,p=p*a%n) 13 insert((p*b%n),i); 14 for(ll i=m;i<=n;i+=m) 15 if((j=find(x=x*p%n))!=-1) return i-j; 16 return -1; 17 }
好了,Judge's Class 终于水完了,继续刷水题去 Bye~