网上看到一个不错的 贴子 ,所以写一篇博客作为学习笔记
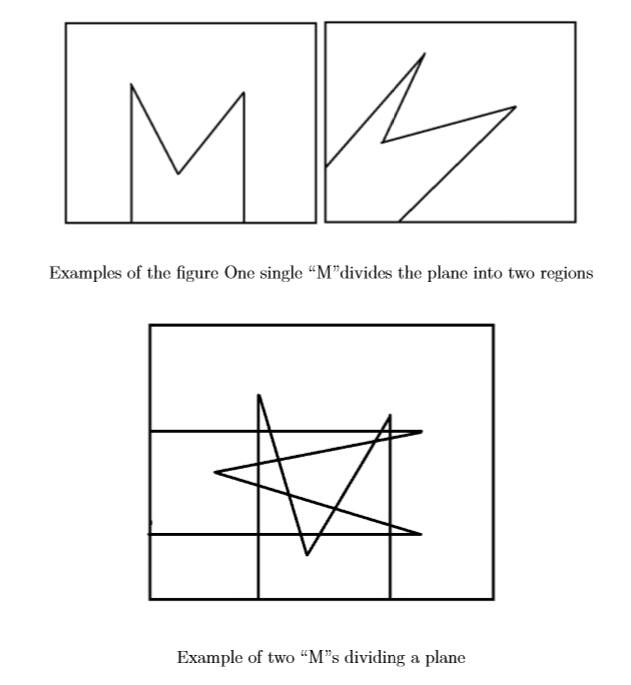
因为要尽可能使得相交后的空间更多,则任意的一对 (M) 应交于不同的位置,否则产生的点数一定更少
故在最优方案下,任意一对 (M) 的交点应该是一样的,由图可得,任意一对的交点数为 (16)
再考虑上每个 (M) 和边框有两个交点,故图中的点数 (V=16cdot C_n^2+2n=8n^2-6n)
而如果再已知边数 (E) ,则可根据欧拉公式 (V-E+F-T=1) 由于三维的 (T=0) ,故即可求解出分割出的面数 (F=E-V+1)
故考虑如何求出边数 (E)
我们考虑一个很极限的情况:图形是近乎无穷大的
而每个 (M) 的中间拐点在接近出发的边框处,两个外边的拐点在接近另一处的边框处,但没有相交
故可以视为 (M) 的四条边是近乎相互平行的四条边
而在之前的假设中,任意一对 (M) 都应该尽可能相交,故 (M) 的四条边都被其他 ((n-1)) 个 (M) 划分出了 (4(n-1)) 个分割点,产生了 (4(n-1)+1) 段边
故四条平行的边,对 (E) 的贡献就是 (4n[4(n-1)+1]=16n^2-12n)
其次,再考虑和边框的交点,每个 (M) 与边框产生 (2) 个交点, (n) 个 (M) 即为 (2n) 个交点,把成环的边框分成了 (2n) 段
最后,再考虑 (M) 的三个拐点。在上面的 (4(n-1)+1) 段边中,我们把它们两边的边视为了不同的边
但实际上,这些拐点并不是交点,因此它们两边的边实际上不能视为不同的边。故每个拐点重复计算了一次,一个 (M) 计算了 (3) 次,总的重复计算了 (3n) 次
最后得到 (E=16n^2-12n-3n+2n=16n^2-13n)
合成得到 (F=E-V+1=8n^2-7n+1) ,考虑秦九韶算法可整理成 (F=(8n-7)n+1)
由于 (nleq 10^{12}) 我们估计一下最后的大小:
该结果为开口向上的二次函数,最大值在端点处取到,显然不是 (1) 处,故为 (8 imes 10^{24}-7 imes 10^{12}+1geq 7 imes 10^{24}) 已经超过 long long 了
long long 的最大值大概在 (10^{18})
不过很显然,答案不超过 (8 imes 10^{24}) ,而 ( ext{lb }(8 imes 10^{24})=3+24 ext{lb }10leq 3+24 ext{lb }16=3+24*4=99leq 128)
因此可以用 __int128 水过去
记得 __int128 不支持输入输出,需要手写即可
【代码】
#include<bits/stdc++.h>
using namespace std;
inline __int128 read(){
register __int128 ans=0;register char c=getchar();while(c<48||c>57) c=getchar();
while(c>=48&&c<=57) ans=ans*10+c-48,c=getchar();
return ans;
}
inline void output(__int128 ans){
char s[128]={0},*p=s+126;
while(ans) *(p--)=ans%10+48,ans/=10;
puts(p+1);
}
int main(){
__int128 T=read(),N;
for(int i=1;i<=T;i++)
N=read(),printf("Case #%d: ",i),output( (8*N-7)*N+1 );
return 0;
}