bzoj1003物流运输 最短路+DP

bzoj1003物流运输

题目描述

物流公司要把一批货物从码头A运到码头B。由于货物量比较大，需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线，以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在，有的时某个码头会无法装卸货物。这时候就必须修改运输路线，让货物能够按时到达目的地。但是修改路线是一件十分麻烦的事情，会带来额外的成本。因此物流公司希望能够订一个n天的运输计划，使得总成本尽可能地小。

输入格式

第一行是四个整数n（1<=n<=100）、m（1<=m<=20）、K和e。n表示货物运输所需天数，m表示码头总数，K表示每次修改运输路线所需成本。接下来e行每行是一条航线描述，包括了三个整数，依次表示航线连接的两个码头编号以及航线长度（>0）。其中码头A编号为1，码头B编号为m。单位长度的运输费用为1。航线是双向的。再接下来一行是一个整数d，后面的d行每行是三个整数P（ 1 < P < m）、a、b（1< = a < = b < = n）。表示编号为P的码头从第a天到第b天无法装卸货物（含头尾）。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头A到码头B的运输路线。

输出格式

包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。

样例

样例输入

5 5 10 8
1 2 1
1 3 3
1 4 2
2 3 2
2 4 4
3 4 1
3 5 2
4 5 2
4
2 2 3
3 1 1
3 3 3
4 4 5

样例输出

32

样例解释

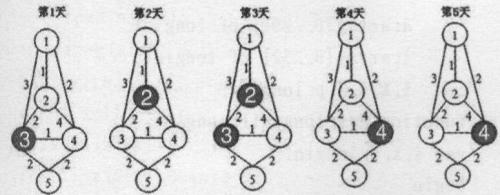
上图依次表示第 1 至第 5 天的情况，阴影表示不可用的码头。

最优方案为：前三天走 1→4→5，后两天走 1→3→5，这样总成本为 (2+2)×3+(3+2)×2+10=32

题解：这道题真心不难，拿来复习一下最短路和dp

我们设cost[i][j]表示i到j这个时间段不换航线的情况下的最小花费，

则：cost[i][j]=dis[m]*(j-i+1),dis[m]是i到j时段起点到终点的最短路

dp[i]表示前i天的最小花费

则：dp[i]=min(dp[j]+k+cost[j+1][i])，j<i;

最后输出dp[n]即可

ps：一开始TLE最后发现是数组开小了

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#define re register
#define MAXN 2005
#define MAXM 205
using namespace std;
int n, m, k, e, d, ans = 0, cost[MAXN][MAXN];  // cost[i][j]表示i到j这个时间段不换航线的情况下的最小花费
bool stop[MAXM][MAXN];                         // stop[i][j]=1表示码头i在第j天不可用
int to[MAXN << 1], nxt[MAXN << 1], w[MAXN << 1], pre[MAXM], tot_e = 0;
void add(int u, int v, int val) {
    tot_e++, w[tot_e] = val, to[tot_e] = v, nxt[tot_e] = pre[u], pre[u] = tot_e;
}
int dis[MAXN];
bool vis[MAXN], lim[MAXN];
queue<int> q;
int spfa(int s, int t) {
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    memset(lim, 0, sizeof(lim));
    for (int i = 1; i <= m; i++)
        for (int j = s; j <= t; j++)
            if (stop[i][j])
                lim[i] = 1;
    q.push(1);
    vis[1] = 1, dis[1] = 0;
    while (!q.empty()) {
        int x = q.front();
        q.pop();
        for (int i = pre[x]; i; i = nxt[i]) {
            int y = to[i];
            if (lim[y])
                continue;
            if (dis[y] > dis[x] + w[i]) {
                dis[y] = dis[x] + w[i];
                if (!vis[y]) {
                    q.push(y);
                    vis[y] = 1;
                }
            }
        }
        vis[x] = 0;
    }
    return dis[m];
}
int dp[MAXN];  // dp[i]表示前i天的最小花费
int main() {
    scanf("%d%d%d%d", &n, &m, &k, &e);
    for (int i = 1, u, v, w; i <= e; i++) {
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w), add(v, u, w);
    }
    scanf("%d", &d);
    for (int i = 1, p, a, b; i <= d; i++) {
        scanf("%d%d%d", &p, &a, &b);
        for (int j = a; j <= b; j++) stop[p][j] = 1;
    }
    for (int i = 1; i <= n; i++)
        for (int j = i; j <= n; j++) {
            cost[i][j] = spfa(i, j);
            if (cost[i][j] != 0x3f3f3f3f)
                cost[i][j] *= (j - i + 1);
        }
    memset(dp, 0x3f, sizeof(dp));
    for (int i = 1; i <= n; i++) {
        dp[i] = cost[1][i];
        for (int j = 1; j < i; j++) {
            if (cost[j + 1][i] != 0x3f3f3f3f)
                dp[i] = min(dp[i], dp[j] + k + cost[j + 1][i]);
        }
    }
    printf("%d", dp[n]);
    return 0;
}