题目描述
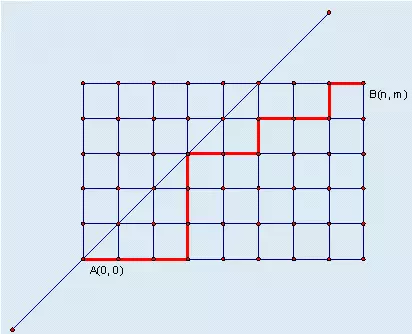
某城市的街道呈网格状,左下角坐标为A(0, 0),右上角坐标为B(n, m),其中n >= m。
现在从A(0, 0)点出发,只能沿着街道向正右方或者正上方行走,且不能经过图示中直线左上方的点,即任何途径的点(x, y)都要满足x >= y,
请问在这些前提下,到达B(n, m)有多少种走法。
输入格式
输出格式
样例
数据范围与提示
卡特兰数折线表示:

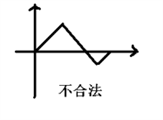
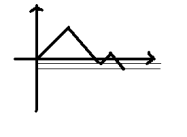
n=m:
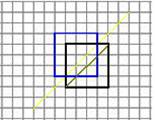
n>m:

博主很懒连打字都不想打了
好吧其实n=m时你会发现是卡特兰数,当n>m时,我们把黑色沿绿线翻折,得到另一块黑色,
如果我们只用卡特兰数,会算上紫框里的部分(由a到c),所以减去
n=m也是一样,只是式子化简一下就是卡特兰数
用到高精,高精你会TLE,所以要把式子化简一下
没啥可说的,普及一下CATALAN数
卡特兰数是组合数学中经常出现在计数问题的数列,
满足:h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)
另一种递推公式:h(n)=$frac{(n-1)*(4*n-2)}{n+1}$
通项公式:h(n)=$C_{2*n}^{n}-C_{2*n}^{n-1}$
h(n)=$frac{C_{2*n}^{n}}{n+1}$
应用:
出栈次序是卡特兰数的一个应用。
我们将入栈视为+1,出栈视为-1,则限制条件为在任意位置前缀和不小于0 。
我们讨论这个问题与卡特兰数有什么关系。
为了方便,我们按入栈的先后顺序将各个元素由1到n编号。
假设最后一个出栈的数为k。 则在k入栈之前,比k小的数一定全部出栈,所以这部分方案数为h(k-1)。
在k入栈之后,比k大的数在k入栈之后入栈,
在k出栈之前出栈,所以这部分的方案数为h(n-k)。
这两部分互不干扰,则方案数为h(k-1)*h(n-k) 枚举k,得到的公式就是卡特兰数的递推公式。
卡特兰数的应用
括号匹配
二叉树计数
有限制的网格路径数
好了先普及这些,放代码:
#include<bits/stdc++.h>
#define re register
#define MAXN 50005
using namespace std;
int n,m;
struct node{
int m[MAXN];
node(){memset(m,0,sizeof(m));}
inline friend void operator *= (node &a,re int b){
int x=0;
for(re int i=1;i<=a.m[0];i++){
re int y=a.m[i]*b+x;
a.m[i]=y%10;
x=y/10;
}
while(x){
a.m[++a.m[0]]=x%10;
x/=10;
}
}
inline friend void operator /= (node &a,re int b){
re int x=0;
for(re int i=a.m[0];i>=1;i--){
x+=a.m[i];
a.m[i]=x/b;
x%=b;
x*=10;
}
while(a.m[a.m[0]]==0&&a.m[0]>1)
a.m[0]--;
}
inline friend node operator - (node a,node b){
node c;
re int i=1;
while((i<=a.m[0])||(i<=b.m[0])){
if(a.m[i]<b.m[i]){
a.m[i]+=10;
a.m[i+1]--;
}
c.m[i]=a.m[i]-b.m[i];
i++;
}
while(c.m[i]==0&&i>1)
i--;
c.m[0]=i;
return c;
}
inline friend void print(node a){
for(re int i=a.m[0];i>=1;i--)
printf("%d",a.m[i]);
puts("");
}
}x;
int main(){
scanf("%d%d",&n,&m);
x.m[0]=x.m[1]=1;
for(re int i=m+1;i<=n+m;i++) x*=i;
x*=(n-m+1);
for(re int i=2;i<=n+1;i++) x/=i;
print(x);
return 0;
}