浅谈FFT(快速博立叶变换)&学习笔记

0XFF---FFT是啥?

FFT是一种DFT的高效算法，称为快速傅立叶变换（fast Fourier transform），它根据离散傅氏变换的奇、偶、虚、实等 特性，对离散傅立叶变换的算法进行改进获得的。 ---百度百科

对于两个多项式 (F(x)) 和 (G(x)) ，要求你将他们乘起来。

那还不简单？直接暴力相乘啊：

设 (F(x)) 的系数数列为 (C)。

(F(x) imes G(x) = C_nx^nG(x) + C_{n-1}x^{n-1}G(x) + C_{n-2}x^{n-2}G(x) cdots C_2x^2G(x) + C_1x^1G(x) + C_0G(x))

这样下来需要做做 (n) 次单项式乘多项式，每次的时间复杂度 (O(n)) ，则总复杂度高达 (O(n^2))

基本上 (n) 上了(4000) 就会被卡吧......那怎么提速呢？

这就需要我们伟大而又神奇的神器：(FFT) (快速博立叶变换)

复杂度就只有 (O(nlogn)) 了。

---

0X1F---FFT的前置知识.

---

1.复数是什么?

我们把形如 (z=a+bi)（ (a,b) 均为实数）的数称为复数，其中 (a) 称为实部， (b) 称为虚部， (i) 称为虚数单位。当虚部等于零时，这个复数可以视为实数；当z的虚部不等于零时，实部等于零时，常称z为纯虚数。复数域是实数域的代数闭包，即任何复系数多项式在复数域中总有根。 复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人 的工作，此概念逐渐为数学家所接受。 ---百度百科

想必大家都知道实数是啥(不知道重读幼儿园吧......)，实数位于数轴上，就像下图这样：

我们稍微观察一下，(1) 是怎么变到 (-1) 的呢？

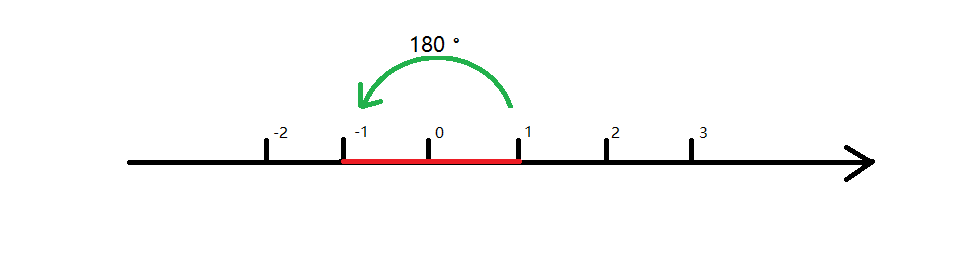
在数轴上转了 (180°)。

如果，是 (90°) 的话，会发生什么呢？

这个时候，会转到 (0) 上面的位置，但是那里，好像没有数啊!

不对，其实是有的，只不过这个数不在实数轴上，而是在虚数轴上！

虚数轴的单位是 (i) ，我们可以这么表示：

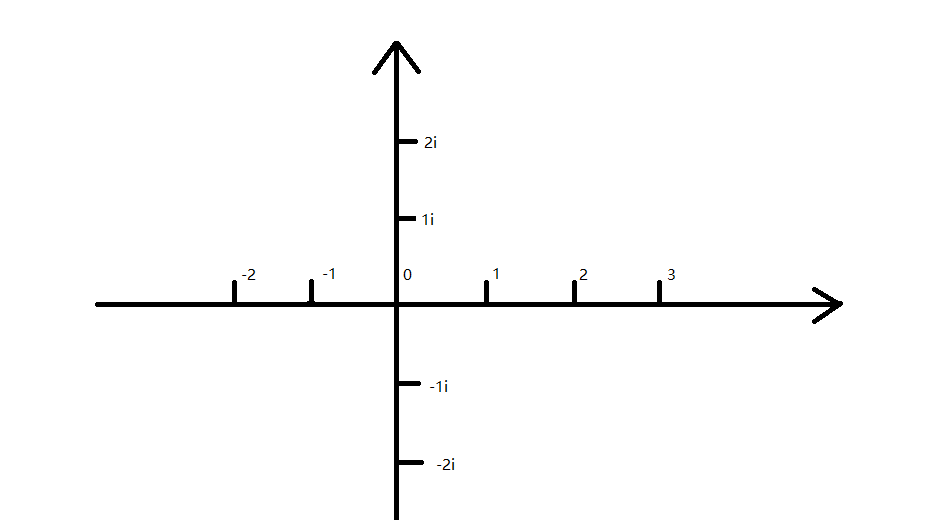
嗯，对。这显然是一个平面坐标系。现在我们的数仅限于数轴上，如果是这个平面坐标系上的一个点怎么表达呢？

对于下面的红色点：

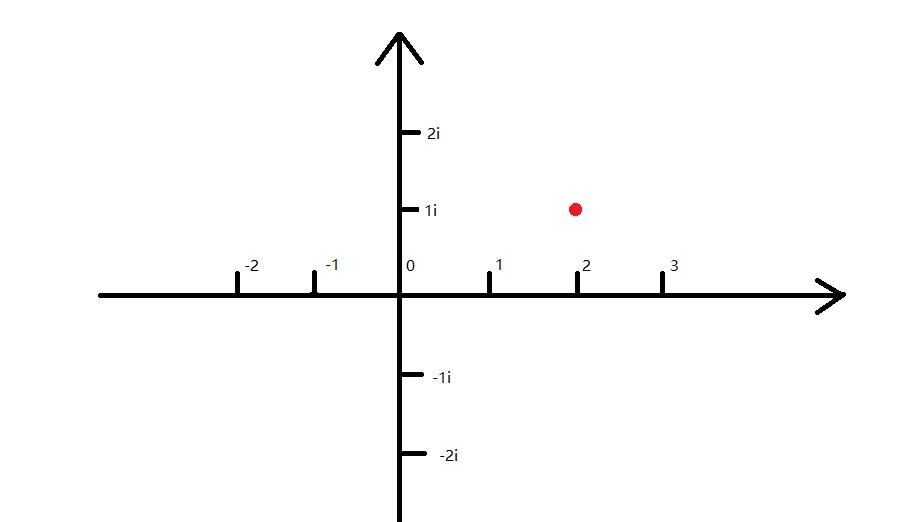
这个点的坐标很容易的可以得到：((2,i)) ，也可以表示成 (2+i) .

你没猜错！这个就叫复数！

一个很重要的结论：复数相乘时，模长相乘，幅角相加！

---

2.点值表示法是什么?

我们用一个二维平面坐标系，在上面画 (N+1) 个点，最终可以解出一个 (n) 元的函数。证明略。

同样，我们可以用 (N-1) 个点来表达一个多项式。

因为点值相乘的复杂度只有 (O(n)) 显然优秀许多。

---

3.单位根是什么?

*n次单位根(n为正整数)是n次幂为1的复数!
*n次单位根(n为正整数)是n次幂为1的复数!
*n次单位根(n为正整数)是n次幂为1的复数!

我们先在复平面上画个点，就像这样：

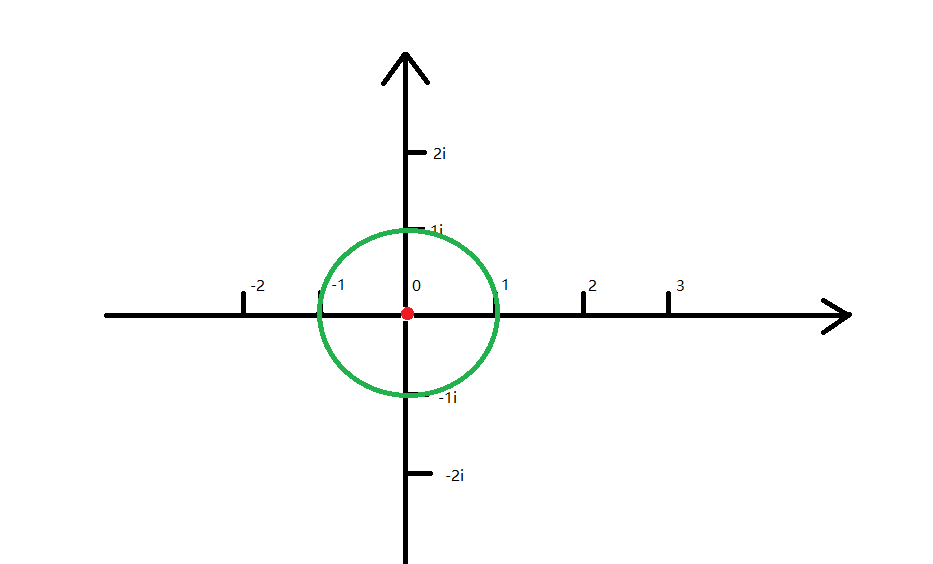
Ta叫做单位圆。

圆边上的任意一点的模长都是 (1).

只有单位圆上的点表示的复数才有可能成为(n)次单位根!

单位根的基本符号：(ω)

一个单位圆，我们将它切成 (n) 份，从 ((1,0)) 开始旋转，每次旋转 (frac{1}{n} imes 360) 度，每次旋转后的点都记为 (ω_{n}^{k})，特别的，(ω_{n}^{0}) 和 (ω_{n}^{n}) 都是 ((1,0)) 点。

还有，当 (k>=n) 或者 (k<0) 时，(ω_{n}^{k}) 也是合法的。

单位根的性质：

(1.) 对于任意的 (n) , (ω_{n}^{0}) 都为 ((1,0)) 点。
(2.) $ω_{n}^{a} imes ω_{n}^{b} = ω_{n}^{a+b} $
(3.) $ω_{an}^{ak} = ω_{n}^{k} $
(4.) $(ω_{n}^{x})y = (ω_{n}^{y})x $
(5.) $ω_{n}^{k+n/2} = -ω_{n}^{k} $ if(n%2==0)

---

0X2F---FFT的求解过程.

• 分治思想很重要！

我们将多项式 (F(x)) 按位置分成两块。

那么变成了(保证n是2的正整数次幂)：

(F(x) = (C_0+C_2x^2+C_4x^4+ cdots +C_{n-2}x^{n-2}) + (C_1x+C_3x^3+C_5x^5+ cdots +C_{n-1}x^{n-1}))

设两个多项式 (F1(x),F2(x))。

(F1(x) = C_0+C_2x+C_4x^2+ cdots +C_{n-2}x^{n/2-1})
(F2(x) = C_1x+C_3x+C_5x^2+ cdots +C_{n-1}x^{n/2-1})

则我们可以得出：

(F(x) = F1(x^2) + F2(x^2) imes x)

设 (k<n/2) ， 将 (ω_{n}^{k}) 带入多项式 (F(x)).

(F(ω_{n}^{k}) = F1((ω_{n}^{k})2) + F2((ω_{n}^{k})^2) imes ω_{n}^{k})

简化得： (F(ω_{n}^{k}) = F1(ω_{n/2}^{k}) + F2(ω_{n/2}^{k}) imes ω_{n}^{k})

再假设 (k<n/2) ，将 (ω_{n}^{k+n/2}) 带入多项式 (F(x)).

(F(ω_{n}^{k+n/2}) = F1((ω_{n}^{k+n/2})2) + F2((ω_{n}^{k+n/2})^2) imes ω_{n}^{k})
(F(ω_{n}^{k+n/2}) = F1(ω_{n}^{2k+n}) + F2(ω_{n}^{2k+n}) imes ω_{n}^{k+n/2})
(F(ω_{n}^{k+n/2}) = F1(ω_{n}^{2k}) + F2(ω_{n}^{2k}) imes ω_{n}^{k+n/2})
(F(ω_{n}^{k+n/2}) = F1(ω_{n/2}^{k}) + F2(ω_{n/2}^{k}) imes ω_{n}^{k+n/2})
(F(ω_{n}^{k+n/2}) = F1(ω_{n/2}^{k}) - F2(ω_{n/2}^{k}) imes ω_{n}^{k})

比较一下两个式子：

• (F(ω_{n}^{k}) = F1(ω_{n/2}^{k}) + F2(ω_{n/2}^{k}) imes ω_{n}^{k})
• (F(ω_{n}^{k+n/2}) = F1(ω_{n/2}^{k}) - F2(ω_{n/2}^{k}) imes ω_{n}^{k})

等式右边只有一个负号的差别!

这两个式子很关键！

---

0X3F---FFT的代码实现.

对于复数的使用

虽然 (C++ STL) 里面有复数 ((complex)) 但是太慢不建议大家使用。

你可以自己手打 (complex)

• 手打的 (complex) :

struct complex{complex(double a=0,double b=0){x=a,y=b;}double x,y;};
complex operator + (complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
complex operator - (complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
complex operator * (complex a,complex b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}

• FFT:

complex a[N],b[N];
inline void FFT(complex *f,int len,short inv){
    if(!len)return;complex f1[len+1],f2[len+2];
    for(int k=0;k<len;++k)f1[k]=f[k<<1],f2[k]=f[k<<1|1];//按位置分
    FFT(f1,len>>1,inv);FFT(f2,len>>1,inv);//递归处理子问题
	complex tmp=complex(cos(PI/len),inv*sin(PI/len)),buf=complex(1,0);
	
	/*tmp:做一次平方后坐标的变换*/ /*buf:初始位置*/
	
	for(RI k=0;k<len;++k){
	    complex t=buf*f2[k];
	    f[k]=f1[k]+t,f[k+len]=f1[k]-t;buf=buf*tmp;//按照公式还原
	}return;
}
//注意，inv的作用是判断是 "系数转点值" 还是 "点值转系数"

(Code) 中提到的公式是这两项：

• (F(ω_{n}^{k}) = F1(ω_{n/2}^{k}) + F2(ω_{n/2}^{k}) imes ω_{n}^{k})
• (F(ω_{n}^{k+n/2}) = F1(ω_{n/2}^{k}) - F2(ω_{n/2}^{k}) imes ω_{n}^{k})

对于文中的"坐标的变换"：

我们依旧来看单位圆：

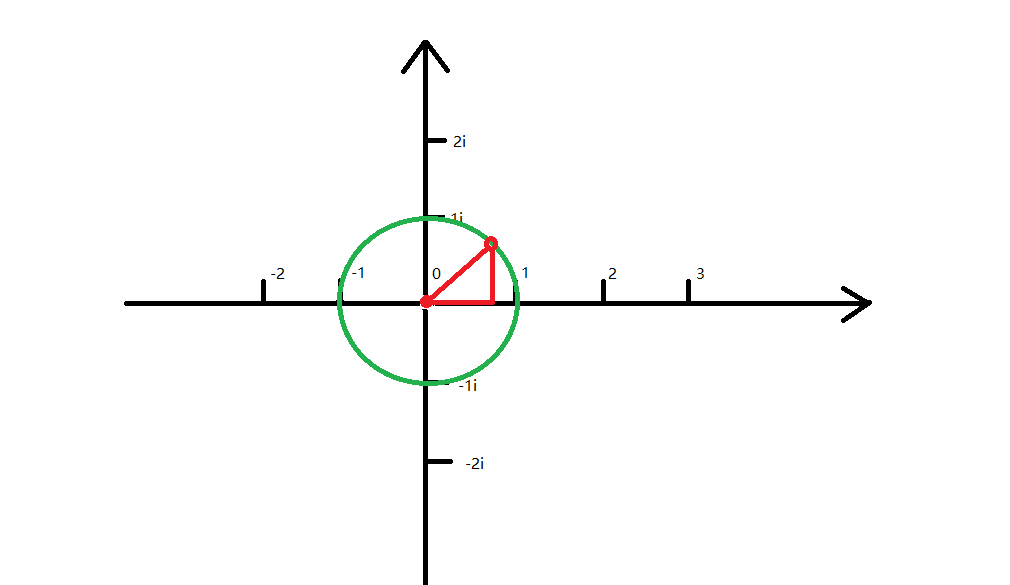
实际上，这个坐标的变换，直接用园中的三角形，运用三角函数就可以得出解了。

过程略.

最后我们得到的结果是：(ω_{n}^{1} = (cos(frac{2π}{n}),sin(frac{2π}{n})))

求出 (ω_{n}^{1}) 后将它乘 (n) 次，可以得到：({ω_{n}^{0},ω_{n}^{1},ω_{n}^{2},ω_{n}^{3}，ω_{n}^{4}，ω_{n}^{5} cdots ω_{n}^{n-1}})

贴出最终的代码：

#include<cstdio>
#include<cmath>
#include<string>
#define ll long long
#define RI register int 
#define inf 0x3f3f3f3f
#define PI 3.1415926535898
using namespace std;
const int N=6e4+2;
template <typename _Tp> inline _Tp max(const _Tp&x,const _Tp&y){return x>y?x:y;} 
template <typename _Tp> inline _Tp min(const _Tp&x,const _Tp&y){return x<y?x:y;}
template <typename _Tp> inline void IN(_Tp&x){
    char ch;bool flag=0;x=0;
	while(ch=getchar(),!isdigit(ch))if(ch=='-')flag=1;
	while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
	if(flag)x=-x;
} 
struct complex{complex(double a=0,double b=0){x=a,y=b;}double x,y;};
complex operator + (complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
complex operator - (complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
complex operator * (complex a,complex b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
complex a[N],b[N];
inline void FFT(complex *f,int len,short inv){
    if(!len)return;complex f1[len+1],f2[len+2];
    for(int k=0;k<len;++k)f1[k]=f[k<<1],f2[k]=f[k<<1|1];
    FFT(f1,len>>1,inv);FFT(f2,len>>1,inv);
	complex tmp=complex(cos(PI/len),inv*sin(PI/len)),buf=complex(1,0); 
	for(RI k=0;k<len;++k){
	    complex t=buf*f2[k];
	    f[k]=f1[k]+t,f[k+len]=f1[k]-t;buf=buf*tmp;
	}return;
}
int n,m;
int main(){
    scanf("%d%d",&n,&m);
    for(RI i=0;i<=n;++i)scanf("%lf",&a[i].x);
    for(RI i=0;i<=m;++i)scanf("%lf",&b[i].x);
    for(m+=n,n=1;n<=m;n<<=1);
    FFT(a,n>>1,1);FFT(b,n>>1,1);
    for(int i=0;i<n;++i)a[i]=a[i]*b[i];
    FFT(a,n>>1,-1);
    for(int i=0;i<=m;++i)printf("%.0f ",fabs(a[i].x)/n);
    putchar('
');
    return 0;
}

听说可以优化，那啥的我还不会，就到这吧.

过了一会儿......

"原来FFT小优化这么简单啊!"

---

0X4F---FFT的一些小优化.

---

不用递归：

递归版(数组下标，先偶后奇，从0开始)：
0  1  2  3  4  5  6  7  --第1层
0  2  4  6 |1  3  5  7  --第2层
0  4 |2  6 |1  5 |3  7  --第3层
0 |4 |2 |6 |1 |5 |3| 7  --第4层

发现了什么吗？

最后的序列是原序列的二进制反转!

比如： (6 = (110)_2) 反过来变成了 ((011)_2 = 3) ！

如何得到二进制翻转后的数列？递推即可!

for(RI i=0;i<n;++i)filp[i]=(filp[i>>1]>>1)|((i&1)?n>>1:0); 
//filp[i] 即为 i 的二进制位翻转

Code:

#include<cstdio>
#include<cmath>
#include<string>
#define ll long long
#define RI register int 
#define inf 0x3f3f3f3f
#define PI 3.1415926535898
using namespace std;
const int N=3e6+2;
int n,m,filp[N]; 
template <typename _Tp> inline _Tp max(const _Tp&x,const _Tp&y){return x>y?x:y;} 
template <typename _Tp> inline _Tp min(const _Tp&x,const _Tp&y){return x<y?x:y;}
template <typename _Tp> inline void IN(_Tp&x){
    char ch;bool flag=0;x=0;
	while(ch=getchar(),!isdigit(ch))if(ch=='-')flag=1;
	while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
	if(flag)x=-x;
} 
struct complex{complex(double a=0,double b=0){x=a,y=b;}double x,y;};
complex operator + (complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
complex operator - (complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
complex operator * (complex a,complex b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
complex a[N],b[N];
inline void FFT(complex *f,short inv){
    for(RI i=0;i<n;++i)if(i<filp[i]){complex tmp=f[i];f[i]=f[filp[i]];f[filp[i]]=tmp;}
    /*换位置*/
    for(RI p=2;p<=n;p<<=1){//每局区间长度
        RI len=p/2;//合并子区间的长度(所以是p/2)
        complex tmp=complex(cos(PI/len),inv*sin(PI/len));
        for(RI k=0;k<n;k+=p){//每局左端点
            complex buf=complex(1,0);
            for(RI l=k;l<k+len;++l){//遍历区间
                complex t=buf*f[len+l];
				f[len+l]=f[l]-t,f[l]=f[l]+t,buf=buf*tmp;//赋值有微小的变化，注意顺序！
            }
        }
    }return;
}
/*主程序不变*/
int main(){
    scanf("%d%d",&n,&m);
    for(RI i=0;i<=n;++i)scanf("%lf",&a[i].x);
    for(RI i=0;i<=m;++i)scanf("%lf",&b[i].x);
    for(m+=n,n=1;n<=m;n<<=1);
    for(RI i=0;i<n;++i)filp[i]=(filp[i>>1]>>1)|((i&1)?n>>1:0); 
    FFT(a,1);FFT(b,1);
    for(RI i=0;i<n;++i)a[i]=a[i]*b[i];
    FFT(a,-1);
    for(RI i=0;i<=m;++i)printf("%.0f ",fabs(a[i].x)/n);
    putchar('
');
    return 0;
}

luogu上的题，递归的总是T最后一个点，改成非递归版的就A了？
emmmmmmmmmmmmmm

---

所有优化全开：

很作死，建议不要轻易尝试[滑稽]

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")

[滑稽][滑稽][滑稽][滑稽][滑稽][滑稽][滑稽][滑稽][滑稽][滑稽][滑稽]

---

最后，因为本人实在太弱了，太蒟了，所以实在写不出啥了。

---

(by Qiuly)