一、引入
首先,堆是一种树型数据结构,在功能上他是用来排序的,因为他的完全二叉树性质,所以他的插入复杂度,删除复杂度最坏情况下是 O(logn) 。虽然是树,但是在大部分时候都是看作队列的,c++ 和 java 的优先队列都是使用堆的原理来实现的。
二、堆的性质
- 堆总是一颗完全二叉树(也就是说任何操作均不会破坏他的完全二叉树性质)。完全二叉树就是说一个节点如果没有左孩子,那么他没有孩子。
- 堆的每个节点都比他的子节点 小/大(具体看是小根堆还是大根堆,我下面讲的是小根堆,小根堆和大根堆差不多,理解其中一个另外一个就很容易了。)
性质一这个性质非常重要,他能简化堆的操作,还能节约空间,或者说就是为了这个才把堆写成完全二叉树。因为这个性质,所以的堆的节点插入和删除都是一层一层来的,而用数组存储完全二叉树时有一个性质,假设树有 n 个节点,那么数组从 1 循环到 n(用数组存树时,我习惯用下标为 1 的元素作根节点,也可以用 0 ),刚好是树的层序遍历,这个手摸一下很快就能发现,那么用数组存储时,插入第 n+1 个节点时,插入点就是 【数组名】[n+1] 的位置,然后再调整,直到满足堆的第二性质。
最后再讲树的数组表示法,父节点 k ,左孩子为 2*k,右孩子为 2*k+1,这个可以用位运算做常数优化,k<<1 和 k<<1|1,这是根节点为 1 时的性质,根节点为 0 就不符合这个性质了,如果不是很明白可以手摸一下。
三、实现环节
首先是数的插入。
插入如图所示,假设所有节点都不需要调整(编号仅为插入顺序,不代表数的大小)
(图是用网站生成之后,自己截的,所以大小有点不一致,强迫症原谅我。)
插入第一个数,存放在数组下标为 1 的元素上(根节点):

插入第二个数,存放在下标为 2 的元素上( 1 的左孩子):
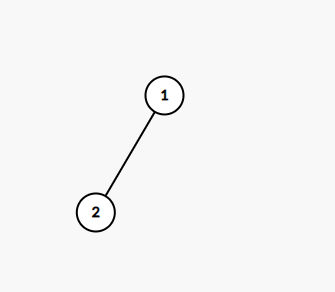
插入第三个数,存放在下标为 3 的元素上(1 的右孩子):

插入第四个数,存放在下标为 4 的元素上(2的左孩子):
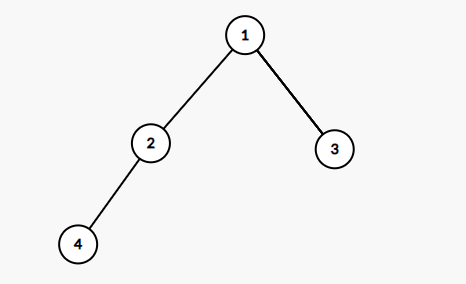
以此类推
当然插入的时候不一定按照顺序来,所以我们插入的时候需要一些调整。在插入一个数之后我们需要判断是否满足堆的第二性质,判断他和父节点的大小关系,如果不满足,就要交换他和父节点直到满足第二性质为止。
如何取得父节点呢,假设 k 是当前节点,k/2就是父节点了,同样可以常数优化成 k>>1。这里利用到了 int 型的自动去尾的特性,在实际编程中我们经常会用到计算机专有的小特性。
插入和调整如图所示:
插入前的树(此时的数字表示这个节点存储的数据):
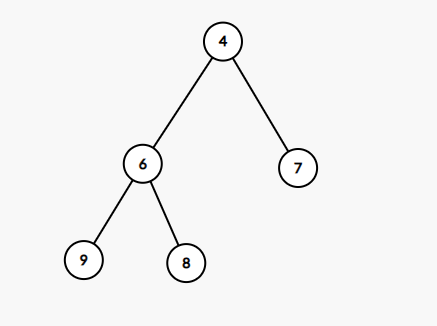
现在我们插入一个 1 :
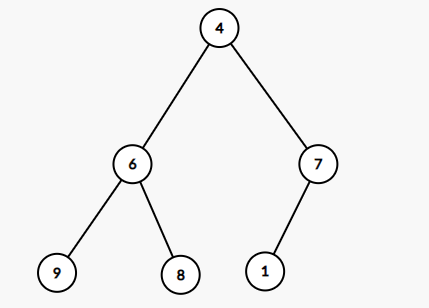
很明显可以看到 1 不符合小根堆的性质,需要向上调整:
第一次调整:
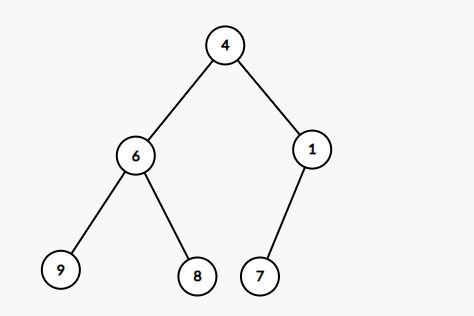
第二次调整:
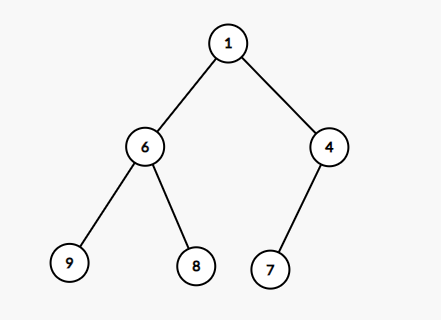
调整结束,重新变回小根堆。
那么插入的代码就可以很容易得到了。
面向对象的思路加模板化可以提高代码的可重复利用性,以后就不必要重复造轮子了,STL 的出现就是这样的想法。
inline void push(T data)//T代表数据类型 { a.push_back(data);//用vector操作更方便,而且空间分配更自由,而且 STL 中的优先队列就是用 vector 作为底层容器,如果不愿意用 vector 就需要一个变量指向数组尾部 unsigned int k = a.size()-1;//最后一个数 while(k > 1)//这里注意必须是大于 1 ,否则可能会把队首和 0 号元素换位置 { if(a[k] >= a[k/2])//不需要进行调整了 break; swap(a[k],a[k/2]);//交换 k /= 2; } }
其次就是弹堆顶操作。
有些朋友再看了之前的代码,应该会想到直接用两个孩子中大的那个数覆盖掉父亲节点,一直做到没有孩子为止。
这样的思路是大错特错的,这样可能会破坏完全二叉树的性质。
所以我们首先用最后一个节点来覆盖掉根节点,然后再向下调整(当然这个还可以扩展到删除任何元素,我们都可以先覆盖再调整)。
删除如图所示:
删除前的树(别回去看了就是之前的图。。。):
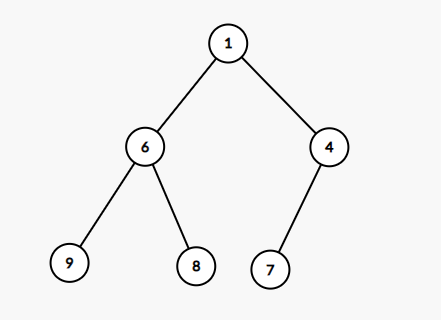
现在我们要删除 1 :
第一步覆盖:

然后记住一定要删除最后一个节点,不然就有两个 7 了
第二步调整,4 和 6 比 4更小,所以 4 和 7 交换位置:
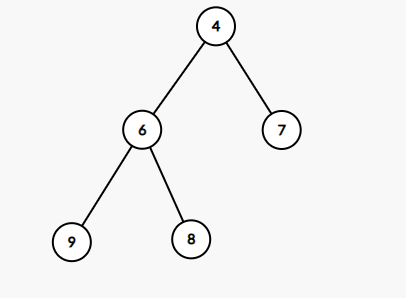
此时 7 下面已经没有孩子节点了,调整结束。
那么调整代码就很容易得到了:
inline void pop() { a[1] = a.back();//覆盖 a.erase(a.end()-1);//删除最后一个元素,-1不能忘,因为 c++ 的区间默认左闭右开,没 -1 会 RE。 unsigned int k = 1,c; unsigned int size = a.size() - 1;//先把 a 的 size 存下来,计算机是很蠢的,每次都会去调用这个函数,先存下来可以优化常数。 while(2*k <= size) { c = 2*k; if(c < size && a[c] > a[c+1])//比较一下左孩子 右孩子谁更小。注意条件是小于 size 。因为他可能没有右孩子,而循环条件只判断了有没有孩子。这里有等于可能会导致 RE。 c++; if(a[k] < a[c])//不需要调整了 break; swap(a[k],a[c]);//交换 k = c; } }
以上就是两个关键操作。接下来是一些简单易懂的辅助函数
inline unsigned int size(){return a.size() - 1;}//返回堆中元素的个数 inline bool empty(){return a.size() == 1;}//判断堆是否为空 inline T top(){return a[1];}//取堆顶 priorue(){a.push_back(0);}//构造函数,先把 0 号位占了,这样子第一个节点就能插在 1 的位置上了。
c++ 实现:
template<class T> class priorue { private: vector<T>a;//头文件记得包含 vector public: inline unsigned int size(){return a.size() - 1;} inline bool empty(){return a.size() == 1;} inline T top(){return a[1];} inline void push(T data) { a.push_back(data); unsigned int k = a.size()-1; while(k > 1) { if(a[k] >= a[k/2]) break; swap(a[k],a[k/2]); k /= 2; } } inline void pop() { a[1] = a.back(); a.erase(a.end()-1); unsigned int k = 1,c; unsigned int size = a.size() - 1; while(2*k <= size) { c = 2*k; if(c<size&&a[c] > a[c+1]) c++; if(a[k] < a[c]) break; swap(a[k],a[c]); k = c; } } priorue(){a.push_back(0);} };
java 实现(本人初学 java,所以 java 代码可能设计的不够成熟,大佬就别在意这个设计问题了)
package priority_queue; import java.util.Scanner; class priority_queue { private int[] heap; private int size = 0; public int top() { return heap[1]; } public int size() { return size; } public boolean empty() { return size == 0; } public void push(int data) { heap[++size] = data; int k = size; while(k > 1) { if(heap[k] >= heap[k/2]) { break; } else { int t = heap[k]; heap[k] = heap[k/2]; heap[k/2] = t; k /= 2; } } } public void pop() { int k = 1; heap[1] = heap[size--]; while(2 * k <= size) { int c = k * 2; if(c < size && heap[c + 1] < heap[c]) c++; if(heap[k] <= heap[c]) break; int t = heap[c]; heap[c] = heap[k]; heap[k] = t; k = c; } } public priority_queue(int size) { heap = new int[size+1]; } }
因为大部分人都是 c++ 党和 java 党,所以 c 的代码就不贴了其实也差不多,算法是互通的嘛 其实就是懒得打
如果你觉得写的还行的话请点个赞。您的一个小小的赞对我来说是个莫大的鼓励
由于作者水平有限,可能会有错误,如果有错误,恳请指正。
如需转载,请附上原作者和出处。虽然估计也没人转载蒟蒻的博客
最后再给大家分享一下可以用来制作树和图的工具,(以上的图都是这么来的)
https://csacademy.com/app/graph_editor/