一:素数

1 int prime[N],p[N],tot; 2 void init() 3 { 4 for(int i=2;i<N;i++) prime[i]=1; 5 for(int i=2;i<N;i++) 6 { 7 if(prime[i]==1) p[++tot]=i; 8 for(int j=1;j<=tot;j++) 9 { 10 prime[i*p[j]]=0; 11 if(i%p[j]==0) break; 12 } 13 } 14 }
二:快速幂

1 LL pow_mod(LL a, LL b, LL p){//a的b次方求余p 2 LL ret = 1; 3 while(b){ 4 if(b & 1) ret = (ret * a) % p; 5 a = (a * a) % p; 6 b >>= 1; 7 } 8 return ret; 9 }
快速乘

1 LL mul(LL a, LL b, LL p){//快速乘,计算a*b%p 2 LL ret = 0; 3 while(b){ 4 if(b & 1) ret = (ret + a) % p; 5 a = (a + a) % p; 6 b >>= 1; 7 } 8 return ret; 9 }
三:gcd和lcm
lcm=a/gcd*b;

1 LL gcd(LL a, LL b){ 2 if(b == 0) return a; 3 else return gcd(b, a%b); 4 } 5 6 LL gcd(LL a, LL b){ 7 return b ? gcd(b, a%b) : a; 8 } 9 //两种都可以
gcd(ka, kb) = k * gcd(a, b)
lcm(ka, kb) = k * lcm(a, b)
lcm(S/a, S/b) = S/gcd(a, b)
四:扩展欧几里得算法
已知 a,b 求 一组解 x,y 满足 ax+by = gcd(a, b) 这个公式

1 void ex_gcd(LL a, LL b, LL &d, LL &x, LL &y) 2 { 3 if(!b) 4 {d = a; x = 1; y = 0;} 5 else 6 { 7 ex_gcd(b, a%b, d, y, x); 8 y -= x*(a/b); 9 } 10 }
五:数论四大定理
1.威尔逊定理:
当且仅当p为素数时:( p -1 )! ≡ -1 ( mod p )
或者这么写( p -1 )! ≡ p-1 ( mod p )
或者说
若p为质数,则p能被(p-1)!+1整除
2.欧拉定理:
若n,a为正整数,且n,a互质,即gcd(a,n) = 1,则
a^φ(n) ≡ 1 (mod n)
φ(n) 是欧拉函数
欧拉函数是求 1到n-1 中 与n互质的数 的数目
3.中国剩余定理
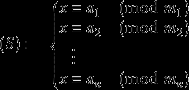
假设整数m1,m2, ... ,mn两两互质,则对任意的整数:a1,a2, ... ,an,方程组 (S)有解

1 #include<cstdio> 2 typedef long long LL; 3 const int N = 100000 + 5; 4 void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){ 5 if (!b) {d = a, x = 1, y = 0;} 6 else{ 7 ex_gcd(b, a % b, y, x, d); 8 y -= x * (a / b); 9 } 10 } 11 LL inv(LL t, LL p){//如果不存在,返回-1 12 LL d, x, y; 13 ex_gcd(t, p, x, y, d); 14 return d == 1 ? (x % p + p) % p : -1; 15 } 16 LL china(int n, LL *a, LL *m){//中国剩余定理 17 LL M = 1, ret = 0; 18 for(int i = 0; i < n; i ++) M *= m[i]; 19 for(int i = 0; i < n; i ++){ 20 LL w = M / m[i]; 21 ret = (ret + w * inv(w, m[i]) * a[i]) % M; 22 } 23 return (ret + M) % M; 24 } 25 int main(){ 26 LL p[3], r[3], d, ans, MOD = 21252; 27 int cas = 0; 28 p[0] = 23; p[1] = 28; p[2] = 33; 29 while(~scanf("%I64d%I64d%I64d%I64d", &r[0], &r[1], &r[2], &d) && (~r[0] || ~r[1] || ~r[2] || ~d)){ 30 ans = ((china(3, r, p) - d) % MOD + MOD) % MOD; 31 printf("Case %d: the next triple peak occurs in %I64d days. ", ++cas, ans ? ans : 21252); 32 } 33 34 }

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 typedef long long LL; 5 typedef pair<LL, LL> PLL; 6 PLL linear(LL A[], LL B[], LL M[], int n) {//求解A[i]x = B[i] (mod M[i]),总共n个线性方程组 7 LL x = 0, m = 1; 8 for(int i = 0; i < n; i ++) { 9 LL a = A[i] * m, b = B[i] - A[i]*x, d = gcd(M[i], a); 10 if(b % d != 0) return PLL(0, -1);//答案不存在,返回-1 11 LL t = b/d * inv(a/d, M[i]/d)%(M[i]/d); 12 x = x + m*t; 13 m *= M[i]/d; 14 } 15 x = (x % m + m ) % m; 16 return PLL(x, m);//返回的x就是答案,m是最后的lcm值 17 }
4.费马小定理:
假如p是质数,若p不能整除a,则 a^(p-1) ≡1(mod p),若p能整除a,则a^(p-1) ≡0(mod p)。
或者说,若p是质数,且a,p互质,那么 a的(p-1)次方除以p的余数恒等于1。
六:逆元
求单个逆元: inv[a]=pow(a,mod-2,mod);
求n个数的逆元: inv[0]=inv[1]=1; inv[i]=(mod-mod/i)*inv[mod%i];
七:欧拉函数

1 #include<cstdio> 2 using namespace std; 3 const int N = 1e6+10 ; 4 int phi[N], prime[N]; 5 int tot;//tot计数,表示prime[N]中有多少质数 6 void Euler(){ 7 phi[1] = 1; 8 for(int i = 2; i < N; i ++){ 9 if(!phi[i]){ 10 phi[i] = i-1; 11 prime[tot ++] = i; 12 } 13 for(int j = 0; j < tot && 1ll*i*prime[j] < N; j ++){ 14 if(i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j]-1); 15 else{ 16 phi[i * prime[j] ] = phi[i] * prime[j]; 17 break; 18 } 19 } 20 } 21 } 22 23 int main(){ 24 Euler(); 25 }
八:卢卡斯定理
求Cnm,用逆元为O(n)的。
但若 n m 特别大,p很小的时候。
C(n, m) % p = C(n / p, m / p) * C(n%p, m%p) % p
九:康托展开
康托的一套算法可以正好产生n!个数字
比如:
123 -> 0
132 -> 1
213 -> 2
231 -> 3
312 -> 4
321 -> 5

1 void cantor(int s[], LL num, int k){//康托展开,把一个数字num展开成一个数组s,k是数组长度 2 int t; 3 bool h[k];//0到k-1,表示是否出现过 4 memset(h, 0, sizeof(h)); 5 for(int i = 0; i < k; i ++){ 6 t = num / fac[k-i-1]; 7 num = num % fac[k-i-1]; 8 for(int j = 0, pos = 0; ; j ++, pos ++){ 9 if(h[pos]) j --; 10 if(j == t){ 11 h[pos] = true; 12 s[i] = pos + 1; 13 break; 14 } 15 } 16 } 17 } 18 void inv_cantor(int s[], LL &num, int k){//康托逆展开,把一个数组s换算成一个数字num 19 int cnt; 20 num = 0; 21 for(int i = 0; i < k; i ++){ 22 cnt = 0; 23 for(int j = i + 1; j < k; j ++){ 24 if(s[i] > s[j]) cnt ++;//判断几个数小于它 25 } 26 num += fac[k-i-1] * cnt; 27 } 28 }
hdu 1430(坑)
