机器学习中的度量——相关系数

      机器学习是时下流行AI技术中一个很重要的方向，无论是有监督学习还是无监督学习都使用各种“度量”来得到不同样本数据的差异度或者不同样本数据的相似度。良好的“度量”可以显著提高算法的分类或预测的准确率，本文中将介绍机器学习中各种“度量”，“度量”主要由两种，分别为距离、相似度和相关系数，距离的研究主体一般是线性空间中点；而相似度研究主体是线性空间中向量；相关系数研究主体主要是分布数据。本文主要介绍相关系数。

1 皮尔逊相关系数——常用的相关系数

      机在统计学中，皮尔逊相关系数（earson correlation coefficient）用于度量两个变量X和Y之间的相关程度（线性相关），其值介于-1与1之间。在自然科学领域中，该系数广泛用于度量两个变量之间的线性相关程度。它是由卡尔·皮尔逊从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来。
对于总体（由许多有某种共同性质的事物组成的集合），给定随机变量(X, y)，总体皮尔逊相关系数的定义为

[{ ho _{X,Y}}{ m{ = }}frac{{{mathop{ m cov}} left( {X,Y} ight)}}{{{sigma _X}{sigma _Y}}}{ m{ = }}frac{{Eleft( {left( {X - {mu _X}} ight)left( {Y - {mu _Y}} ight)} ight)}}{{{sigma _X}{sigma _Y}}} ]

      机其中cov(X,Y)是随机变量X和随机变量Y之间的协方差
      机σx是随机变量X的方差
      机σy是随机变量Y的方差
      机μx是随机变量X的均值
      机μy是随机变量Y的均值

      机对于同样本来说，给定样本对{(x1, y1), (x2,y2), …, (xn, yn)} ，样本皮尔逊相关系数的定义为

[{r_{x,y}}{ m{ = }}frac{{sumlimits_{i = 1}^n {left( {{x_i} - ar x} ight)left( {{y_i} - ar y} ight)} }}{{sqrt {sumlimits_{i = 1}^n {{{left( {{x_i} - ar x} ight)}^2}} } sqrt {sumlimits_{i = 1}^n {{{left( {{y_i} - ar y} ight)}^2}} } }} = frac{{nsumlimits_{i = 1}^n {{x_i}{y_i}} - sumlimits_{i = 1}^n {{x_i}} sumlimits_{i = 1}^n {{y_i}} }}{{sqrt {nsumlimits_{i = 1}^n {x_i^2} - {{left( {sumlimits_{i = 1}^n {{x_i}} } ight)}^2}} sqrt {nsumlimits_{i = 1}^n {y_i^2} - {{left( {sumlimits_{i = 1}^n {{y_i}} } ight)}^2}} }} ]

      机其中n是样本数量
      机Xi, yi是第i个独立的样本数据
      机x是所有xi的均值
      机y是所有yi的均值

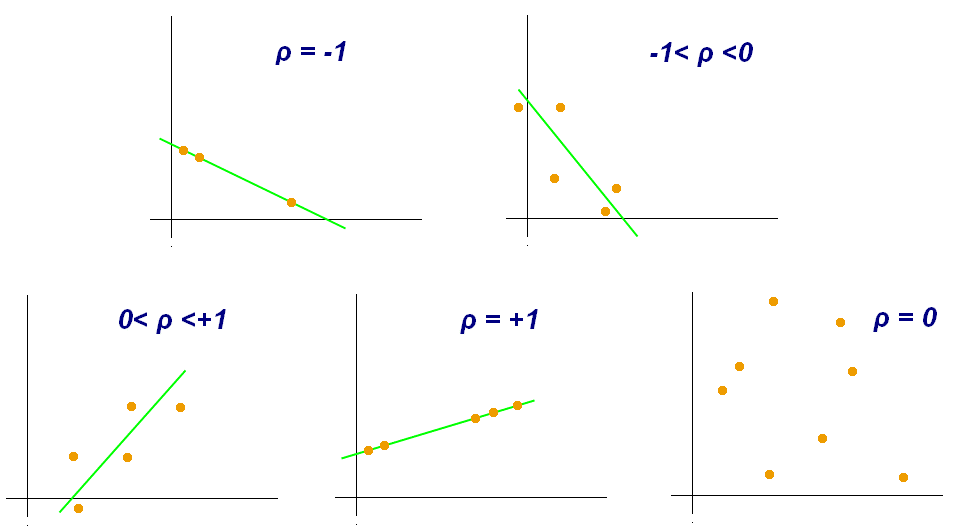
图1 具有不同相关系数值（ρ）的散点图示例
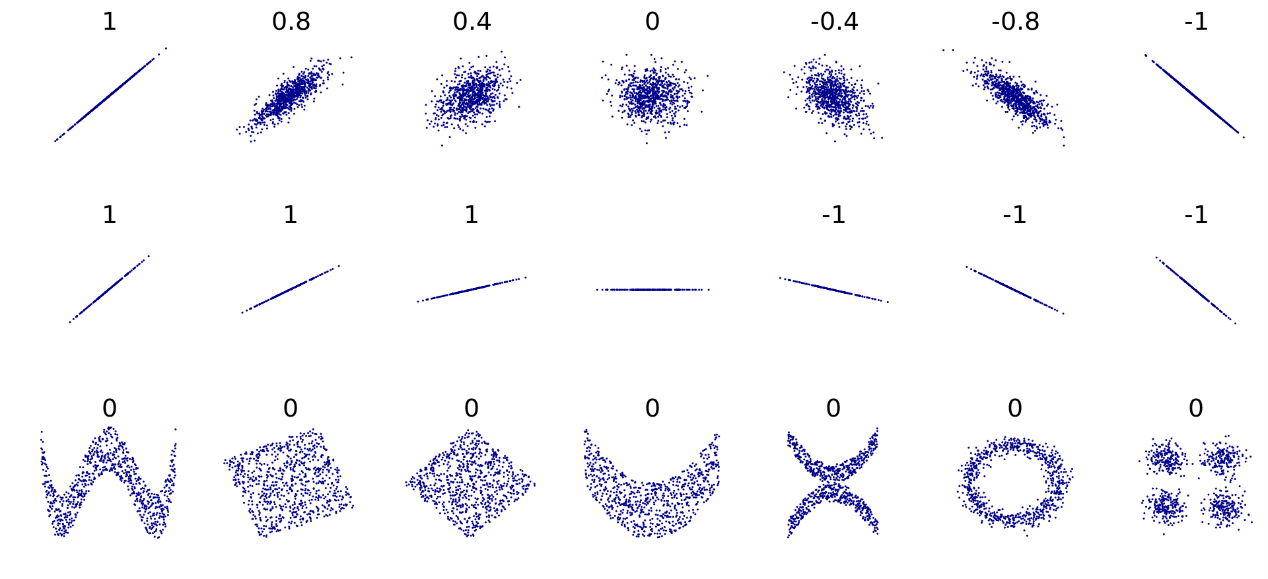
图2 几组点集的相关系数

2 Phi相关系数——二元变量的相关性

      机在统计学里，“Phi相关系数”（Phi coefficient）（符号表示为φ）是测量两个二元变数之间相关性的工具，由卡尔·皮尔森所发明 [1]。他也发明了与Phi相关系数有密切关联的皮尔森卡方检定（Pearson's chi-squared test。一般所称的卡方检验），以及发明了测量两个连续变数之间相关程度的皮尔森相关系数。Phi相关系数在机器学习的领域又称为Matthews相关系数。

      机首先将两个变数排成2×2列联表，注意 1 和 0 的位置必须如同下表，若只变动 X 或只变动 Y 的 0/1 位置，计算出来的Phi相关系数会正负号相反。Phi相关系数的基本概念是：两个二元变数的观察值若大多落在2×2列联表的“主对角线”字段，亦即若观察值大多为(X,Y) =(1,1), (0,0)这两种组合，则这两个变数呈正相关。反之，若两个二元变数的观察值大多落在“非对角线”字段，对应于2×2列联表，亦即若观察值大多为(X,Y) =(0,1), (1,0)这两种组

	Y=1	Y=0	总计
X=1	n11	n10	a1
X=2	n01	n00	a2
总计	b1	b2	n

      机其中 n11, n10, n01, n00都是非负数的字段计次值，它们加总为n ，亦即观察值的个数。由上面的表格可以得出 X 和 Y 的 Phi相关系数如下：

      机一个简单的实例：研究者欲观察性别与惯用手的相关性。虚无假设是：性别与惯用手无相关性。观察对象是随机抽样出来的个人，身上有两个二元变数（性别 X ，惯用手 Y），X 有两种结果值（男=1／女=0），Y也有两种结果值（右撇子=1／左撇子=0）。观察两个二元变数的相关性可以使用Phi相关系数。假设简单随机抽样100人，得出如下的2×2列联表：

	男=1	女=0	总计
右=1	43	44	87
左=2	7	6	13
总计	50	50	100

      机假设−0.0297相关系数检定为显著，在本例对变数 1/0 的指定下，代表身为男性与身为右撇子有轻微的负相关，也就是男性右撇子的比例略低于女性右撇子的比例；或者反过来说，男性左撇子的比例略高于女性左撇子的比例。