正交排列法
说明:正交表是数学中统计学的专业发明
提示:
1)做为测试人员只需要能够选择合适的正交表,并且能够将正交表应用于测试即可
2)正交表是应用的工具,不需要背诵,不需要计算
一、应用场合
在界面中有多个控件,控件之间有多种组合关系,如果组合的数量巨大(一般超过20种),没有必要将所有组合都测试,可以通过正交排列法将组合中最优,最少的组合进行测试。
问题:判定表和正交排列法的异同?
都可以测试控件之间的组合情况
判定表适合测试组合数量比较少(一般少于20种组合的会选择判定表)
正交排列法适合测试组合数量较多的(一般多于20种)
判定表要分析控件之间的组合和限制关系,而正交排列表只需分析控件间组合
二、解析正交排列法
正交表公式:
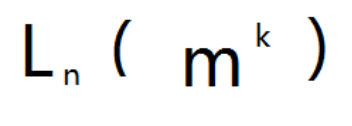
L(Line):行
n:表示正交表的行数
提示:正交表确定后,n值是固定的,不需要测试人员计算
m:表示正交表中数据的最大值
测试时:m表示每个控件的取值个数
K:表示正交表的列数
测试时:k表示参与组合的控件的个数
三、正交排列法的测试步骤
步骤1:分析需求,将参与组合的控件以及每个控件的取值列到excel表格中
步骤2:选择合适的正交表
其实就是确定m值和k值的过程
M值:表示每个控件的取值个数 ,案例中 M=3
K值:参与组合的控件的个数,案例中 k=4
所以要选择的正交表是:3的4次幂的
步骤3:应用正交表(映射)
主要就是将控件和控件的取值与正交表的列标题和列的取值进行替换
1)将控件名称与正交表的列标题(因子)部分进行替换
2)将每个控件的取值跟对应列的数值(状态)进行替换
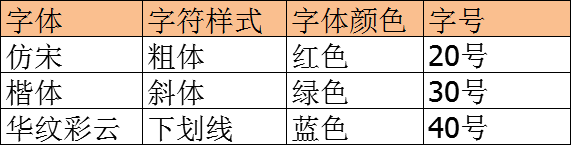
步骤4:根据生成的正交排列表,编写测试用例。
每行是一种控件组合,写1条用例

总结正交表
1、正交表是优选出最少、最优的测试组合,但是毕竟没有测试所有的组合,所以可能存在遗漏缺陷的风险,如果时间允许,可以补充测试。
2、正交表的局限:
1)正交表的数量有限(9张)
|
(1)L4(23)
|
列号
|
1
|
2
|
3
|
|
试验号
|
|
1
|
1
|
1
|
1
|
|
2
|
1
|
2
|
2
|
|
3
|
2
|
1
|
2
|
|
4
|
2
|
2
|
1
|
(2)L8(27)
|
列号
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
试验号
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
2
|
1
|
1
|
1
|
2
|
2
|
2
|
2
|
|
3
|
1
|
2
|
2
|
1
|
1
|
2
|
2
|
|
4
|
1
|
2
|
2
|
2
|
2
|
1
|
1
|
|
5
|
2
|
1
|
2
|
1
|
2
|
1
|
2
|
|
6
|
2
|
1
|
2
|
2
|
1
|
2
|
1
|
|
7
|
2
|
2
|
1
|
1
|
2
|
2
|
1
|
|
8
|
2
|
2
|
1
|
2
|
1
|
1
|
2
|
(3)L12(211)
|
列号
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
试验号
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
2
|
1
|
1
|
1
|
1
|
1
|
2
|
2
|
2
|
2
|
2
|
2
|
|
3
|
1
|
1
|
2
|
2
|
2
|
1
|
1
|
1
|
2
|
2
|
2
|
|
4
|
1
|
2
|
1
|
2
|
2
|
1
|
2
|
2
|
1
|
1
|
2
|
|
5
|
1
|
2
|
2
|
1
|
2
|
2
|
1
|
2
|
1
|
2
|
1
|
|
6
|
1
|
2
|
2
|
2
|
1
|
2
|
2
|
1
|
2
|
1
|
1
|
|
7
|
2
|
1
|
2
|
2
|
1
|
1
|
2
|
2
|
1
|
2
|
1
|
|
8
|
2
|
1
|
2
|
1
|
2
|
2
|
2
|
1
|
1
|
1
|
2
|
|
9
|
2
|
1
|
1
|
2
|
2
|
2
|
1
|
2
|
2
|
1
|
1
|
|
10
|
2
|
2
|
2
|
1
|
1
|
1
|
1
|
2
|
2
|
1
|
2
|
|
11
|
2
|
2
|
1
|
2
|
1
|
2
|
1
|
1
|
1
|
2
|
2
|
|
12
|
2
|
2
|
1
|
1
|
2
|
1
|
2
|
1
|
2
|
2
|
1
|
(4)L9(34)
|
列号
|
1
|
2
|
3
|
4
|
|
试验号
|
|
1
|
1
|
1
|
1
|
1
|
|
2
|
1
|
2
|
2
|
2
|
|
3
|
1
|
3
|
3
|
3
|
|
4
|
2
|
1
|
2
|
3
|
|
5
|
2
|
2
|
3
|
1
|
|
6
|
2
|
3
|
1
|
2
|
|
7
|
3
|
1
|
3
|
2
|
|
8
|
3
|
2
|
1
|
3
|
|
9
|
3
|
3
|
2
|
1
|
|
|
(5)L16(45)
|
列号
|
1
|
2
|
3
|
4
|
5
|
|
试验号
|
|
1
|
1
|
1
|
1
|
1
|
1
|
|
2
|
1
|
2
|
2
|
2
|
2
|
|
3
|
1
|
3
|
3
|
3
|
3
|
|
4
|
1
|
4
|
4
|
4
|
4
|
|
5
|
2
|
1
|
2
|
3
|
4
|
|
6
|
2
|
2
|
1
|
4
|
3
|
|
7
|
2
|
3
|
4
|
1
|
2
|
|
8
|
2
|
4
|
3
|
2
|
1
|
|
9
|
3
|
1
|
3
|
4
|
2
|
|
10
|
3
|
2
|
4
|
3
|
1
|
|
11
|
3
|
3
|
1
|
2
|
4
|
|
12
|
3
|
4
|
2
|
1
|
3
|
|
13
|
4
|
1
|
4
|
2
|
3
|
|
14
|
4
|
2
|
3
|
1
|
4
|
|
15
|
4
|
3
|
2
|
4
|
1
|
|
16
|
4
|
4
|
1
|
3
|
2
|
|
|
(6)L25(56)
|
列号
|
1
|
2
|
3
|
4
|
5
|
6
|
|
试验号
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
2
|
1
|
2
|
2
|
2
|
2
|
2
|
|
3
|
1
|
3
|
3
|
3
|
3
|
3
|
|
4
|
1
|
4
|
4
|
4
|
4
|
4
|
|
5
|
1
|
5
|
5
|
5
|
5
|
5
|
|
6
|
2
|
1
|
2
|
3
|
4
|
5
|
|
7
|
2
|
2
|
3
|
4
|
5
|
1
|
|
8
|
2
|
3
|
4
|
5
|
1
|
2
|
|
9
|
2
|
4
|
5
|
1
|
2
|
3
|
|
10
|
2
|
5
|
1
|
2
|
3
|
4
|
|
11
|
3
|
1
|
3
|
5
|
2
|
4
|
|
12
|
3
|
2
|
4
|
1
|
3
|
5
|
|
13
|
3
|
3
|
5
|
2
|
4
|
1
|
|
14
|
3
|
4
|
1
|
3
|
5
|
2
|
|
15
|
3
|
5
|
2
|
4
|
1
|
3
|
|
16
|
4
|
1
|
4
|
2
|
5
|
3
|
|
17
|
4
|
2
|
5
|
3
|
1
|
4
|
|
18
|
4
|
3
|
1
|
4
|
2
|
5
|
|
19
|
4
|
4
|
2
|
5
|
3
|
1
|
|
20
|
4
|
5
|
3
|
1
|
4
|
2
|
|
21
|
5
|
1
|
5
|
4
|
3
|
2
|
|
22
|
5
|
2
|
1
|
5
|
4
|
3
|
|
23
|
5
|
3
|
2
|
1
|
5
|
4
|
|
24
|
5
|
4
|
3
|
2
|
1
|
5
|
|
25
|
5
|
5
|
4
|
3
|
2
|
1
|
|
|
(7)L8(4×24)
|
列号
|
1
|
2
|
3
|
4
|
5
|
|
实验号
|
|
1
|
1
|
1
|
1
|
1
|
1
|
|
2
|
1
|
2
|
2
|
2
|
2
|
|
3
|
2
|
1
|
1
|
2
|
2
|
|
4
|
2
|
2
|
2
|
1
|
1
|
|
5
|
3
|
1
|
2
|
1
|
2
|
|
6
|
3
|
2
|
1
|
2
|
1
|
|
7
|
4
|
1
|
2
|
2
|
1
|
|
8
|
4
|
2
|
1
|
1
|
2
|
|
|
(8)L12(3×24)
|
列号
|
1
|
2
|
3
|
4
|
5
|
|
试验号
|
|
1
|
1
|
1
|
1
|
1
|
1
|
|
2
|
1
|
1
|
1
|
2
|
2
|
|
3
|
1
|
2
|
2
|
1
|
2
|
|
4
|
1
|
2
|
2
|
2
|
1
|
|
5
|
2
|
1
|
2
|
1
|
1
|
|
6
|
2
|
1
|
2
|
2
|
2
|
|
7
|
2
|
2
|
1
|
2
|
2
|
|
8
|
2
|
2
|
1
|
2
|
2
|
|
9
|
3
|
1
|
2
|
1
|
2
|
|
10
|
3
|
1
|
1
|
2
|
1
|
|
11
|
3
|
2
|
1
|
1
|
2
|
|
12
|
3
|
2
|
2
|
2
|
1
|
|
|
(9)L16(44×23)
|
列号
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
试验号
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
2
|
1
|
2
|
2
|
2
|
1
|
2
|
2
|
|
3
|
1
|
3
|
3
|
3
|
2
|
1
|
2
|
|
4
|
1
|
4
|
4
|
4
|
2
|
2
|
1
|
|
5
|
2
|
1
|
2
|
3
|
2
|
2
|
1
|
|
6
|
2
|
2
|
1
|
4
|
2
|
1
|
2
|
|
7
|
2
|
3
|
4
|
1
|
1
|
2
|
2
|
|
8
|
2
|
4
|
3
|
2
|
1
|
1
|
1
|
|
9
|
3
|
1
|
3
|
4
|
1
|
2
|
2
|
|
10
|
3
|
2
|
4
|
3
|
1
|
1
|
1
|
|
11
|
3
|
3
|
1
|
2
|
2
|
2
|
1
|
|
12
|
3
|
4
|
2
|
1
|
2
|
1
|
2
|
|
13
|
4
|
1
|
4
|
2
|
2
|
1
|
2
|
|
14
|
4
|
2
|
3
|
1
|
2
|
2
|
1
|
|
15
|
4
|
3
|
2
|
4
|
1
|
1
|
1
|
|
16
|
4
|
4
|
1
|
3
|
1
|
2
|
2
|
|
| |
2)要求每个控件中取值个数相同,但是实际应用中很难遇到。(很多应用都不相同)
3、正交表的特性(均匀、平均):
1)每列中不同的数值出现次数均等
2)任意两列中,每一行会形成1个有序数对,则每个有序数对出现的次数均等
四、正交表的强化应用
--没有合适的正交表
1、k值不合适—k值(控件个数)如果没有正好符合的值,那么选择最接近的大一点的,用不到的列可以删除。
例如:3的3次幂的正交表没有,可以选择3的4次幂的正交表,多余1列可以删除。
2、m值—每个控件的取值个数(M值)不同,可以使用以下两种方式解决:
1)少数服从多数原则
就是控件的取值个数相等的最多的那个控件的m值(例如:案例中m=3的控件个数最多,所以m值就等于3)
分析:m=3,k=4所以要选择3的4次幂的正交表
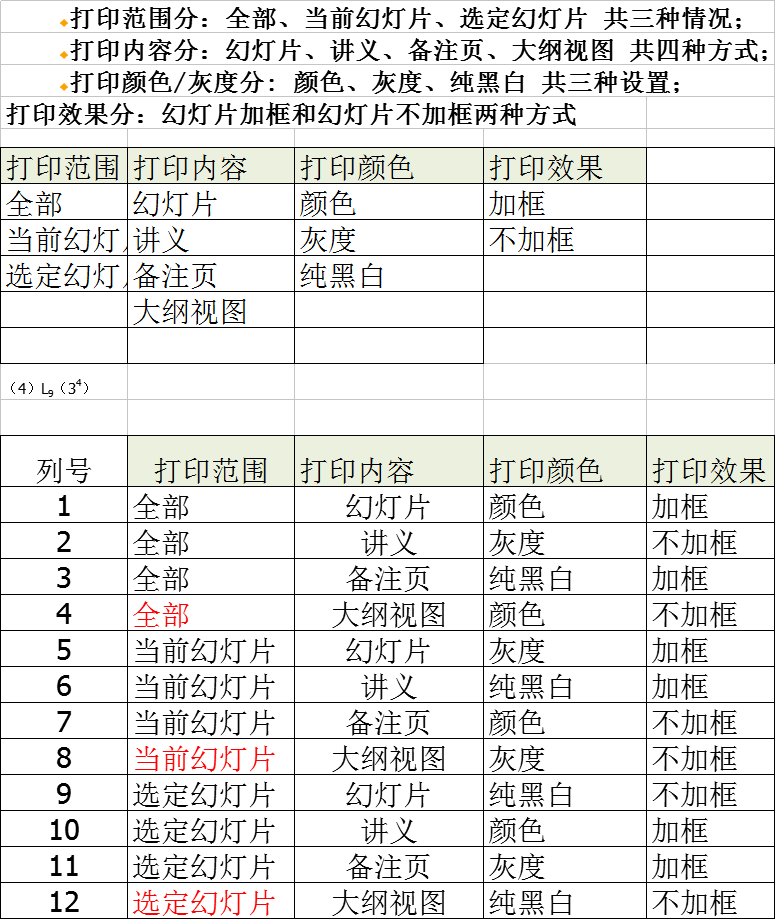
2)最大值原则(建议)
哪个控件的取值数最多,那么m值就是那个控件的取值个数
分析案例:
K=4,m=4(最大)==》理论上应该选择4的4次幂的正交表,但是没有,所以最终选择:4的5次幂的正交表,多余的1列删除即可。
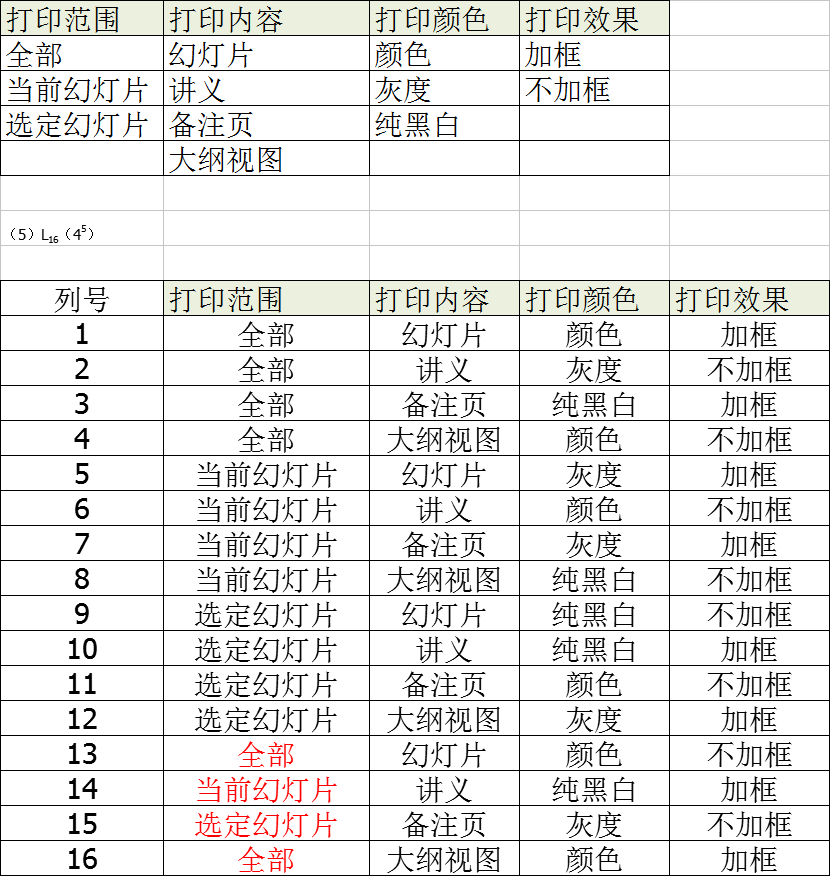
方法总结:
如果有多余的列,删除即可
先把能映射的地方映射好
把每列多出的机会,尽量均匀的分配给该列的各个取值
最后还要检查是否有完全一样的组合,如果有要适当处理(删或改,建议改)
选择正交表时最优先的是选择正合适的正交表,当没有合适的正交表时,再去考虑选择最接近的正交表
问题:正交排列法在实际测试中常用于测试什么功能?
常用于
1)测试属性配置
2)测试软件的兼容性问题
扩展:补码
计算机中整数是以补码存储的:
正整数:
一个正整数的补码和其原码相同
负整数:
将该数取绝对值
计算绝对值原码
将原码按位取反
+1