比赛链接:https://atcoder.jp/contests/abc205
A - kcal
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout << fixed << setprecision(15);
double a, b;
cin >> a >> b;
cout << a * b / 100 << "
";
return 0;
}
B - Permutation Check
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin >> n;
vector<bool> have(n);
for (int i = 0; i < n; i++) {
int x;
cin >> x;
--x;
have[x] = true;
}
cout << (count(have.begin(), have.end(), true) == n ? "Yes" : "No") << "
";
return 0;
}
C - POW
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int a, b, c;
cin >> a >> b >> c;
auto cal = [](int a, int b) {
return a > b ? '>' : (a == b ? '=' : '<');
};
cout << (c % 2 == 0 ? cal(abs(a), abs(b)) : cal(a, b)) << "
";
return 0;
}
D - Kth Excluded
题意
从小到大给出 (n) 个正整数,问这些数外的第 (k) 大正整数。
题解
计算第 (i) 个数对当前位最小值 (i) 的溢出情况,二分第一个溢出不小于 (k) 的位置,取前面的数及其溢出情况即可。
代码
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, q;
cin >> n >> q;
vector<long long> a(n + 1);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
vector<long long> exceed(n + 1);
for (int i = 1; i <= n; i++) {
exceed[i] = a[i] - i;
}
while (q--) {
long long k;
cin >> k;
int pos = lower_bound(exceed.begin(), exceed.end(), k) - exceed.begin();
cout << a[pos - 1] + (k - exceed[pos - 1]) << "
";
}
return 0;
}
E - White and Black Balls
题意
有 (n) 个白球和 (m) 个黑球,现要将这些球排成一排,要求
- 在所有长度的前缀中,白球的个数均不多于黑球 (k) 个
问有多少种排列方式。
题解
与 CF1536C 的思想类似,将球的添加视作平面上点的移动,不妨将白球看作纵坐标 (y) ,黑球看作横坐标 (x) ,本题即从 ((0, 0)) 到 ((m, n)) 的移动过程,共有 (C_{m + n}^{m}) 种排列方式。
又有 (y le x + k) ,即:

因为不合法的情况(路径)一定会与 (y = x + k + 1) 有交点,不妨将 ((0, 0)) 关于该直线对称,得到点 ((- k - 1, k + 1)) ,不合法的情况即转化为从 ((- k - 1, k + 1)) 移动到 ((m, n)) 的情况,共有 (C_{m + n}^{m + k + 1}) 种情况。

综上,除去一开始白球比黑球多 (k) 个无解的情况,答案为 (C_{m + n}^{m} - C_{m + n}^{m + k + 1}) 。
代码
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e6 + 10;
constexpr int MOD = 1e9 + 7;
int fac[N], inv[N];
int binpow(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = 1LL * res * a % MOD;
a = 1LL * a * a % MOD;
b >>= 1;
}
return res;
}
int C(int n, int m){
if(m < 0 or m > n) return 0;
return 1LL * fac[n] * inv[m] % MOD * inv[n - m] % MOD;
}
void Init(){
fac[0] = 1;
for (int i = 1; i < N; i++) fac[i] = 1LL * fac[i - 1] * i % MOD;
inv[N - 1] = binpow(fac[N - 1], MOD - 2);
for (int i = N - 2; i >= 0; i--) inv[i] = 1LL * inv[i + 1] * (i + 1) % MOD;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
Init();
int n, m, k;
cin >> n >> m >> k;
if (n - m > k) {
cout << 0 << "
";
} else {
cout << (C(m + n, m) - C(m + n, m + k + 1) + MOD) % MOD << "
";
}
return 0;
}
F - Grid and Tokens
题意
给出一个 (h imes w) 的网格,有 (n) 个人,第 (i) 个人可以选择 (a_i sim c_i) 行 (b_i sim d_i) 列中的某个网格,一个网格只能被一个人选择,问最多有多少人可以都选到一个网格。
题解
将问题转化为最大流问题,每个人可选择一个网格即转化为容量为 (1) 的边 ((u_i, v_i)) ,可选择的行即转化为 (u_i) 前的结点 (r_{a_i sim c_i}) ,可选择的列即转化为 (v_i) 后的结点 (c_{b_i sim d_i}) ,多人可选择即转化为 (r_i) 前的超级源点 (src) , (c_i) 后的超级汇点 (dst) ,两者间的最大流即最多有多少人可以都选到一个网格。

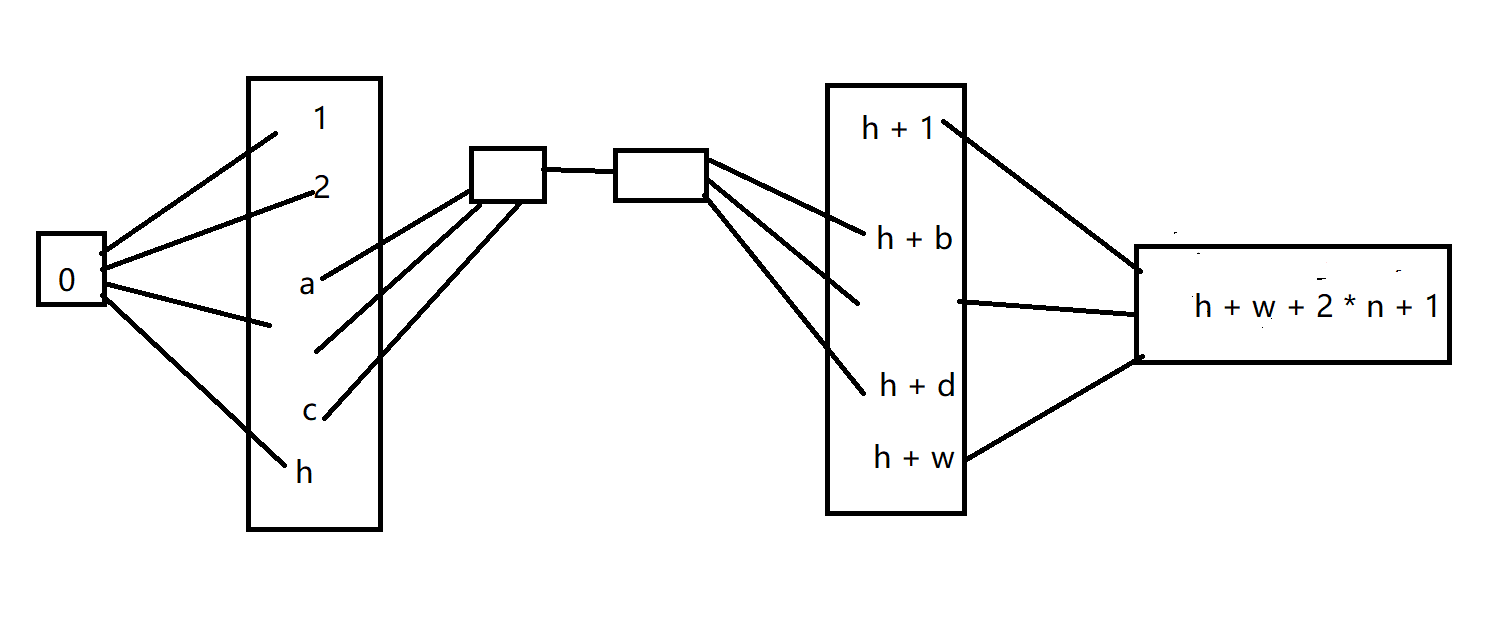
代码
#include <bits/stdc++.h>
#include <atcoder/maxflow>
using namespace std;
using namespace atcoder;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int h, w, n;
cin >> h >> w >> n;
map<int, int> row, col, u, v;
for (int i = 0; i < h; i++) {
row[i] = i + 1;
}
for (int i = 0; i < w; i++) {
col[i] = i + 1 + h;
}
for (int i = 0; i < n; i++) {
u[i] = i + 1 + h + w;
}
for (int i = 0; i < n; i++) {
v[i] = i + 1 + h + w + n;
}
int src = 0, dst = h + w + 2 * n + 1;
mf_graph<int> graph(dst + 1);
for (int i = 0; i < h; i++) {
graph.add_edge(src, row[i], 1);
}
for (int i = 0; i < w; i++) {
graph.add_edge(col[i], dst, 1);
}
for (int i = 0; i < n; i++) {
int a, b, c, d;
cin >> a >> b >> c >> d;
--a, --b;
graph.add_edge(u[i], v[i], 1);
for (int j = a; j < c; j++) {
graph.add_edge(row[j], u[i], 1);
}
for (int j = b; j < d; j++) {
graph.add_edge(v[i], col[j], 1);
}
}
cout << graph.flow(src, dst) << "
";
return 0;
}
参考
D:
https://atcoder.jp/contests/abc205/editorial/2079
E:
https://atcoder.jp/contests/abc205/editorial/2080
F:
https://atcoder.jp/contests/abc205/editorial/2081
https://codeforces.com/blog/entry/91733?#comment-803511
后记
三门大作业和一堆实验终于都做完啦ヽ(✿゚▽゚)ノ
剩下的就只剩在充裕的时间里复习准备期末考试了,好耶( ̄▽ ̄)
时间真是快啊,不知不觉学长学姐们都已经毕业了,祝学长学姐们学业有成,工作顺利 ~
明年这个时候就该自己啦 ╰( ̄ω ̄o)