论分治与归并思想

归并排序

要想了解归并思想，就离不开对归并排序的理解，从前看别人的代码百思不得其解，后来看到一张图片顿时领悟，附下：

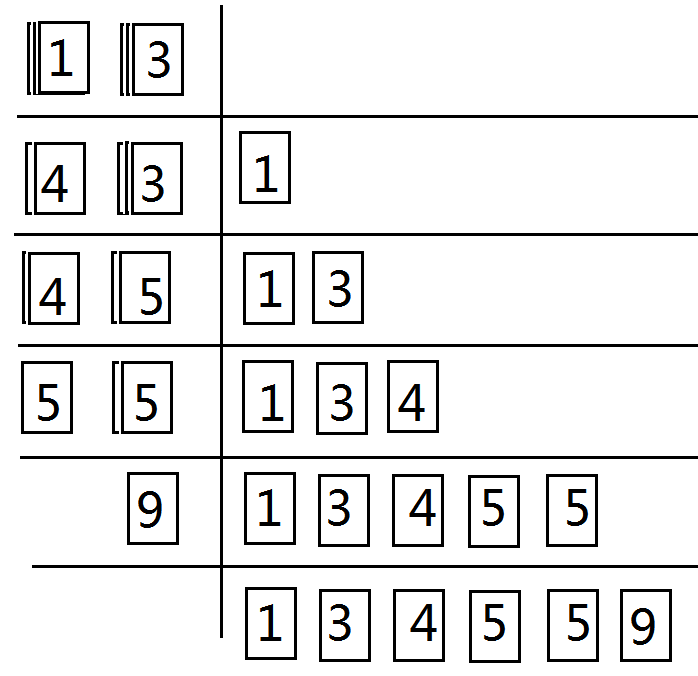
每次比较两个数组，注意可以是一个数组的两个不同的区间，每次将较小的数存储在一个临时数组中，这样就完成了归并排序。当然，前提是这两个数组是有序的，那么，问题是，如何让这两个数组是有序的呢，这就用到了递归。

    merge_sort(left, mid);
    merge_sort(mid+1, right);

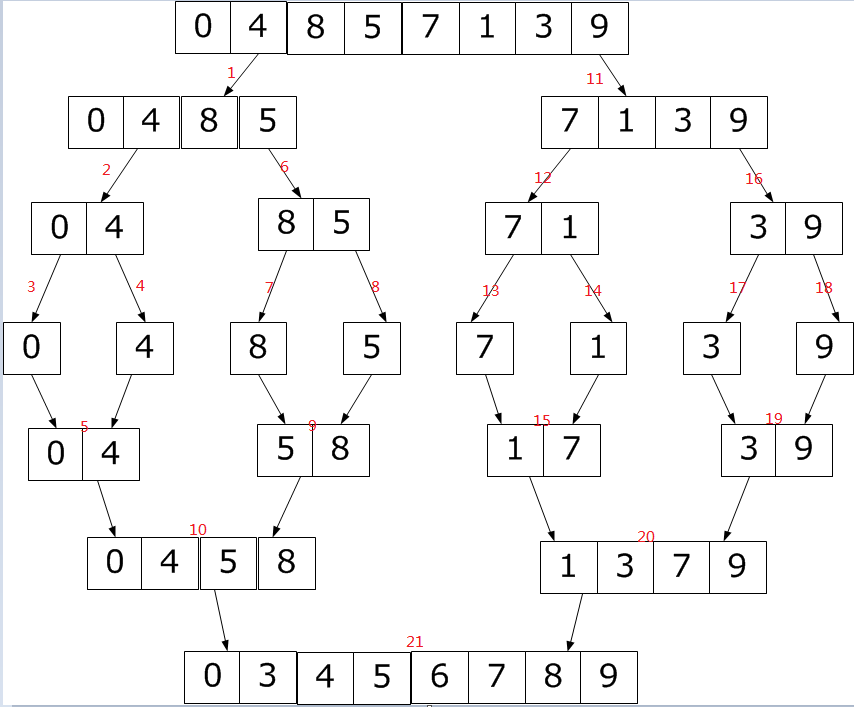
为什么要用递归来实现呢，看下一张图片。

例题

如果只是说理论就显得苦涩难懂，下面贴一个来自洛谷的题目，小试身手。
https://www.luogu.org/problem/P1908
详细讲解已经在代码注释中标明

#include<bits/stdc++.h>
using namespace std;
int N;
int a[100000+10], temp[100000+10];
long long ans = 0;          //ans用于记录逆序对的数量
void merge_sort(int l, int r)
{
    if(l == r) return ;
    int k = 0 ,mid = (l + r)/2;
    merge_sort(l, mid);             
    merge_sort(mid+1, r);
    //注意一定要先递归，这样就可以保证l ~ mid区间、mid + 1 ~ r区间已经完成了从小到大的排序
    int i = l, j = mid + 1;
    while(i <= mid && j <= r)
    {
        if(a[i] < a[j])
            temp[k++] = a[i++];       //将较小的数字存储在临时数组中
        else 
        {
            temp[k++] = a[j++];
            ans += mid - i + 1;     //因为a[i]-a[mid]按递增顺序排列 所以a[j]之前有mid-i+1对逆序对

        }
    }
    while(i <= mid)         //如果a[i...mid]有剩余
        temp[k++] = a[i++];     
    while(j <= r)           //如果a[j...r]有剩余
        temp[k++] = a[j++];
    for(k = 0; k <= (r - l); k++)
        a[l + k] = temp[k];         //这里就完成了两块区间的有序归并

}
int main()
{
    std::ios::sync_with_stdio(false);
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    cin >> N;
    memset(a, 0, sizeof(a));
    memset(temp, 0, sizeof(temp));
    for(int i = 0; i < N; i++)
        cin >> a[i];
    merge_sort(0, N-1);
    cout << ans << endl;
}

以上代码同样可以用于排序（采用了分治排序）

参考博客：https://www.cnblogs.com/mrblug/p/5763138.html