【软件18-循环队列及综合】

判断题

1-1

F：将向量空间想象为一个首尾相接的圆环，并称这种向量为循环向量。存储在其中的队列称为循环队列（Circular Queue）。这种循环队列可以以单链表的方式来在实际编程应用中来实现。因此，循环队列是一个抽象的数据结构，而单向循环链表或循环数组是具体的实现方式，不是数据结构本身。<分析摘录自链接https://blog.csdn.net/Invokar/article/details/80010758>

单选题

2-2

这里注意人家的要求，用头指针和队列个数size代替一般队列的表示方法，这样就不用考虑尾指针了，最多可以直接填满。

2-3

这是一般的循环队列的表示，注意末尾要保留一个。

编程题

7-1

关于这道题目，模拟即可，需要定义两个结构体数组，一个是存窗口的，包括在此窗口排队的人数以及最后结束时间，另一个是存人的，包括其到达时间和处理时间。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
struct Person{
    int T, P;
};
struct Window{
    int num_person;
    int endtime;
};
int N, T, P, K;
Person p[1000+10];
Window w[11];
int main()
{
    // freopen("input.txt", "r", stdin);
    // freopen("output.txt", "w", stdout);
    scanf("%d", &N);
    for(int i = 0; i < N; i++)
    {
        scanf("%d %d", &T, &P);
        if(P > 60)
            P = 60;
        p[i].T = T;
        p[i].P = P;
    }
    scanf("%d", &K);
    for(int i = 0; i < K; i++)
    {
        w[i].num_person = 0;
        w[i].endtime = 0;
    }

    int sum_time = 0, max_time = 0, end_time = 0;
    for(int i = 0; i < N; i++)
    {
        int minwindow = 1e9, idx = -1;
        bool Wait = true;
        for(int j = 0; j < K; j++)
        {
            if(p[i].T >= w[j].endtime)
            {
                w[j].num_person++;
                Wait = false;
                w[j].endtime = p[i].T + p[i].P;
                break;
            }
            else        //寻找等待时间最小的窗口
            {
                if(minwindow > w[j].endtime)
                {
                    minwindow = w[j].endtime;
                    idx = j;
                }
            }
        }
        if(Wait)
        {
            sum_time += minwindow - p[i].T;
            max_time = max(max_time, minwindow - p[i].T);
            w[idx].endtime += p[i].P;   
            w[idx].num_person++;
        }
    }
    for(int i = 0; i < K; i++)
    {
        if(w[i].endtime > end_time)
            end_time = w[i].endtime;
    }
    printf("%.1lf %d %d
", (double)sum_time / (double)N, max_time, end_time);
    for(int i = 0; i < K; i++)
    {
        if(i != 0) printf(" ");
        printf("%d",w[i].num_person);
    }
}

7-2

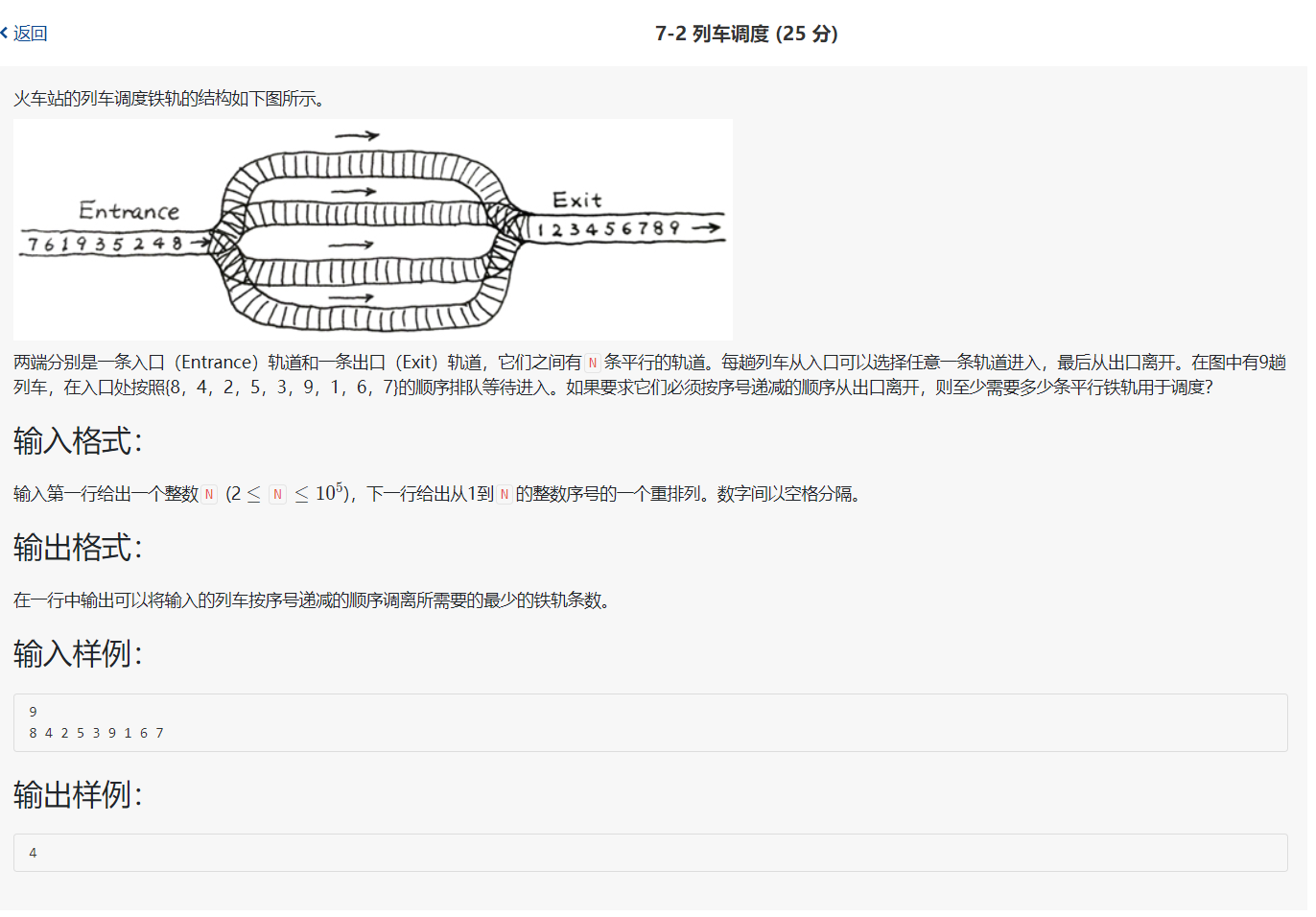
该题目目前不会，

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<set>
using namespace std;
int N, num;
set<int> p;
int main()
{
    // freopen("input.txt", "r", stdin);
    // freopen("output.txt", "w", stdout);
    scanf("%d", &N);
    scanf("%d", &num);
    p.insert(num);
    --N;
    while(N--)
    {
        scanf("%d", &num);
        if(p.upper_bound(num) != p.end())
            p.erase(p.upper_bound(num));
        p.insert(num);
    }
    cout << p.size() << endl;
}