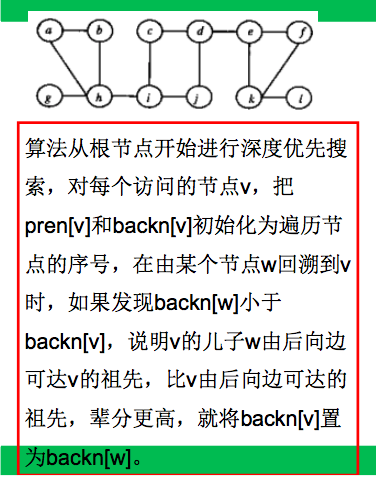
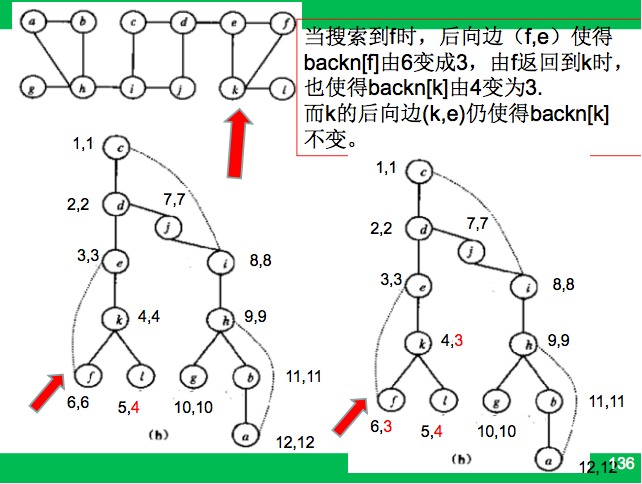
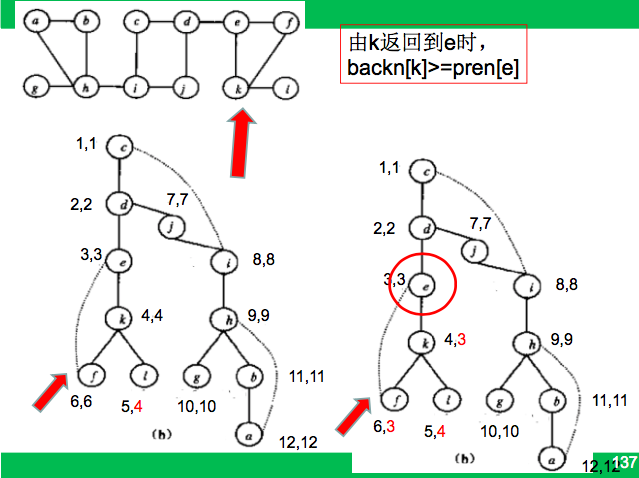
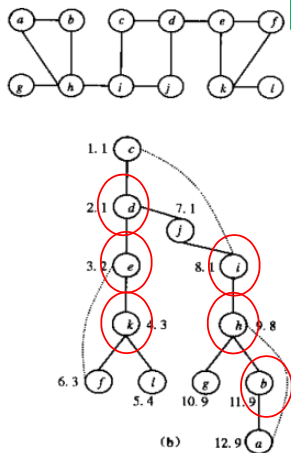
定义:图G(V,E)是连通图,顶点集S是V的子集,若删除S中的所有顶点,将是图不连通,称S是图G的割集。若S={v},则称v为图G的割点(或结合点)。
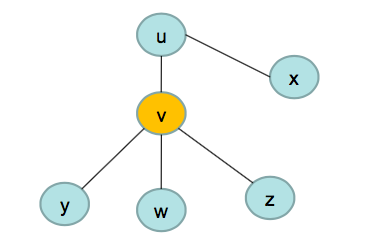
如果一个无向图没有结合点,该图称为双连通图
结合点的性质:
性质1: 当且仅当深度优先搜索树的根结点至少有两个以上儿子,则根结点是结合点。
性质2: 当且仅当深度优先搜索树中,v的每以一个儿孙结点不能通过后向边到达v结点的祖先结点,则结点v是结合点
在进行遍历时,有向图的边,可以分为:
树边:深度优先搜索生成树中的边;
后向边: 与边(u, v)相关联的顶点u和v,在深度优先搜索树中,v是u的祖先,在从(u, v)出发进行搜索时,v已被标记过为访问过的结点;
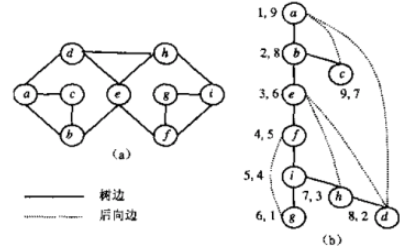
求结合点的方法:
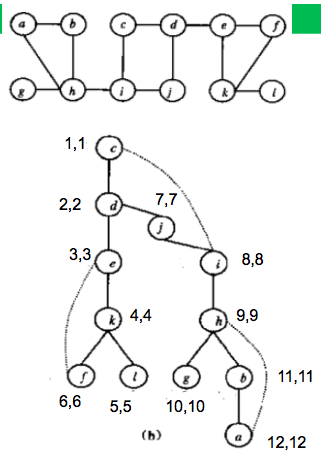
对每个顶点v,设立变量pren[v]和backn[v],pren[v]是顶点v的遍历序号,backn[v]是顶点v的后向可达顶点的最小遍历序号;
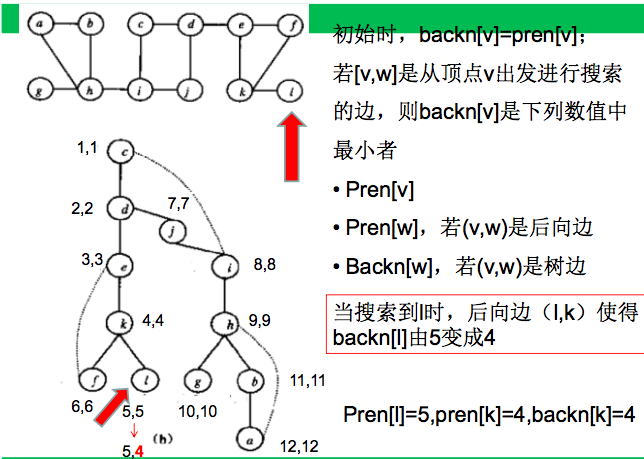
初始时,backn[v] = pren[v];
若[v,w]是从顶点v出发进行搜索的边,则backn[v]是下列数值中最小者
* pren[v]
* pren[w],若(v,w)是后向边
* backn[w],若(v, w)是树边
只要顶点v有一个儿子w,使得backn[w]>=pren[v],则说明v的儿孙w不能通过后向边达到v的祖先,因此v是接合点。
算法流程:
从v顶点开始搜索:
(1)把v标记为访问过,初始化pren[v],backn[v],使得指针p指向v的邻接表;
(2)若p为空,处理搜索到的接合点的计数,算法结束;否则,令p指向的邻接点是w;若(v, w)是树边,执行步骤3),否则执行5)
(3)从w出发递归调用深度优先搜索算法,若v是根结点,按照性质1判定v是否为接合点,否则更新v的后向可达顶点的遍历序号,按性质2判定v是否为接合点;
(4)使得p指向下一个邻接点,转步骤2)
(5)若(v, w)是后向边,更新v的后向可达顶点顶点的遍历序号,转步骤4)