0.PTA得分截图

1.本周学习总结
1.1 总结线性表内容
- 顺序表结构体定义、顺序表插入、删除的代码操作等
- 顺序表结构体定义:即定义一个结构体,结构体中再定义一个数组和数组长度。在输入数据的同时对数据进行排序,也可在输入完所有数据后再用冒泡排序法等方式对数据进行重新排序,使表中各个元素满足顺序递增或递减。
- 代码内容:
typedef int ElemType;
typedef struct
{ ElemType data[MaxSize]; //存放顺序表元素
int length ; //存放顺序表的长度
} List;
typedef List *SqList;
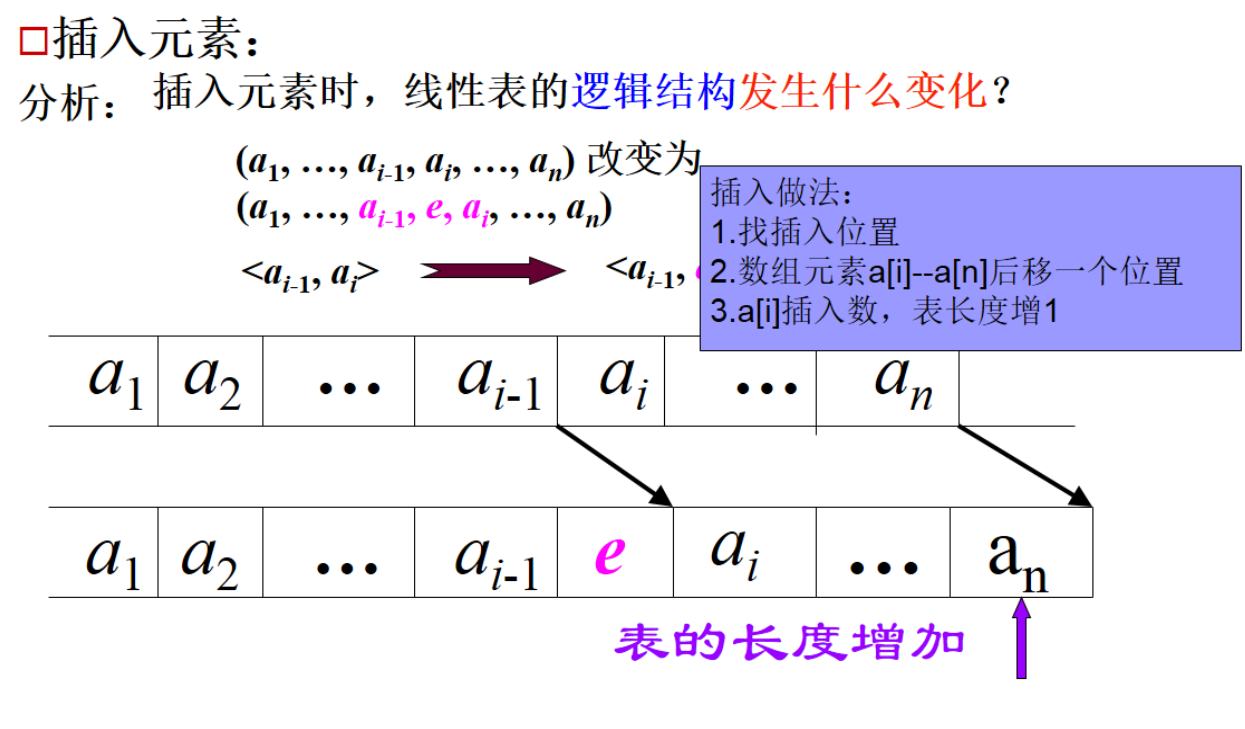
- 顺序表插入:在顺序表中插入一数据,为保证插入后数据仍有序排列,首先要找到插入位置。找到插入位置后,将从该位置起往后的所有数据(包括该位置)全部往后移一个位置,然后给要插入的位置赋值即可。注意:插入完一个新数据后,表的长度要加一!!!
- 主要代码内容及图解(pta 6-2有序表插入数据):
for (i = 0; i < L->length ; i++)
{
if (L->data[i] <= x && L->data[i + 1] >= x)
{
for (j = L->length; j > i; j--)
{
L->data[j] = L->data[j - 1];
}
L->data[i + 1] = x;
L->length+=1;
flag = 1;
break;
}
}
- 顺序表的删除:首先找到要删除的数据位置,然后从该位置起往后的所有数据(包括该位置),全部依次往前移动一个位置,即用后一个的数据来覆盖前一个数据达到删除该位置数据的效果。
- 主要代码内容及图解(pta 6-1删除区间数据):
for (i = 0; i < L->length-1; i++)
{
if (L->data[i] >= min && L->data[i] <= max)
{
for (k = i; k < L->length-1; k++)
{
L->data[k] = L->data[k + 1];
}
L->length--;
i--;
}
}

- 链表结构体定义、头插法、尾插法、链表插入、删除操作
-
链表结构体定义:链表结构体中除目的数据外,还包含一个后继指针,用来指向下一个节点。
-
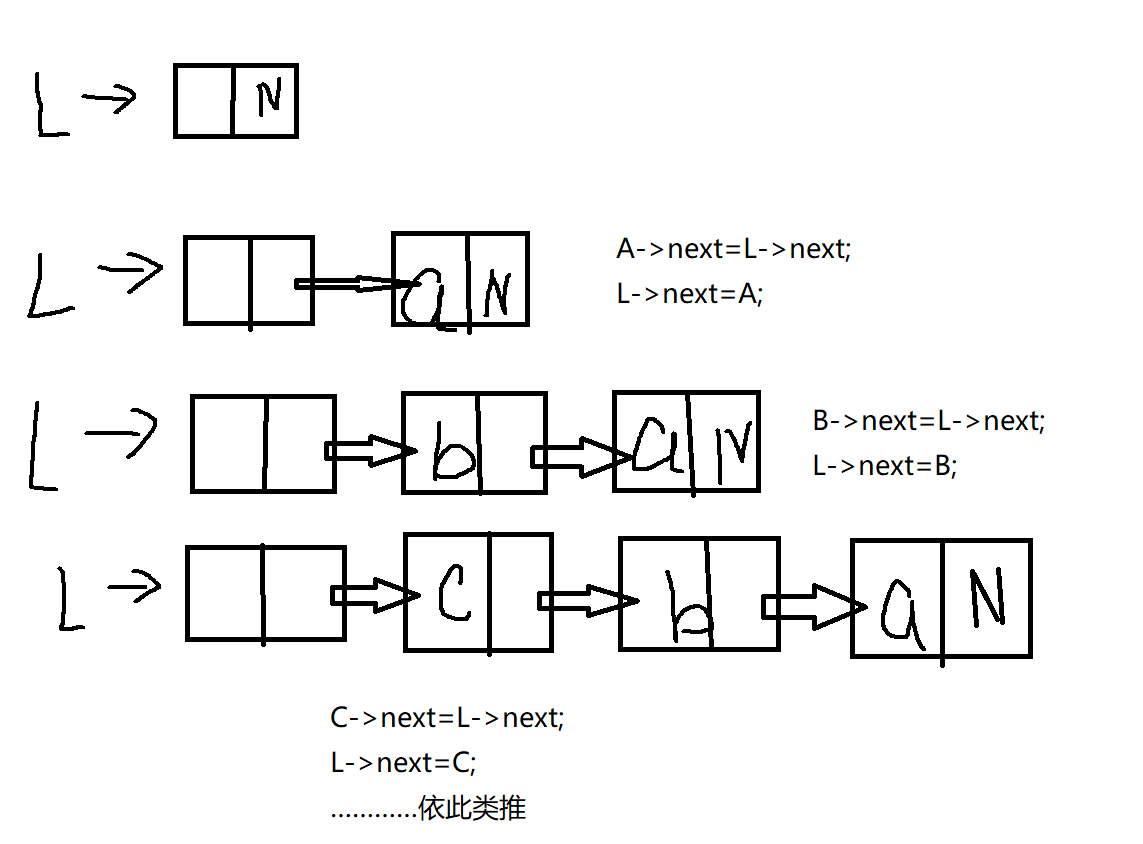
头插法:即在插入节点时将节点插入到头节点后,这样可以使插入的数据逆序存放。
-
主要代码及图解(pta 6-5):
-
for (i = 0; i < n; i++)
{
cin >> data;
if ((p = new LNode) == NULL)
{
cout << "system error!";
}
p->data = data;
p->next = head->next;
head->next = p;
}
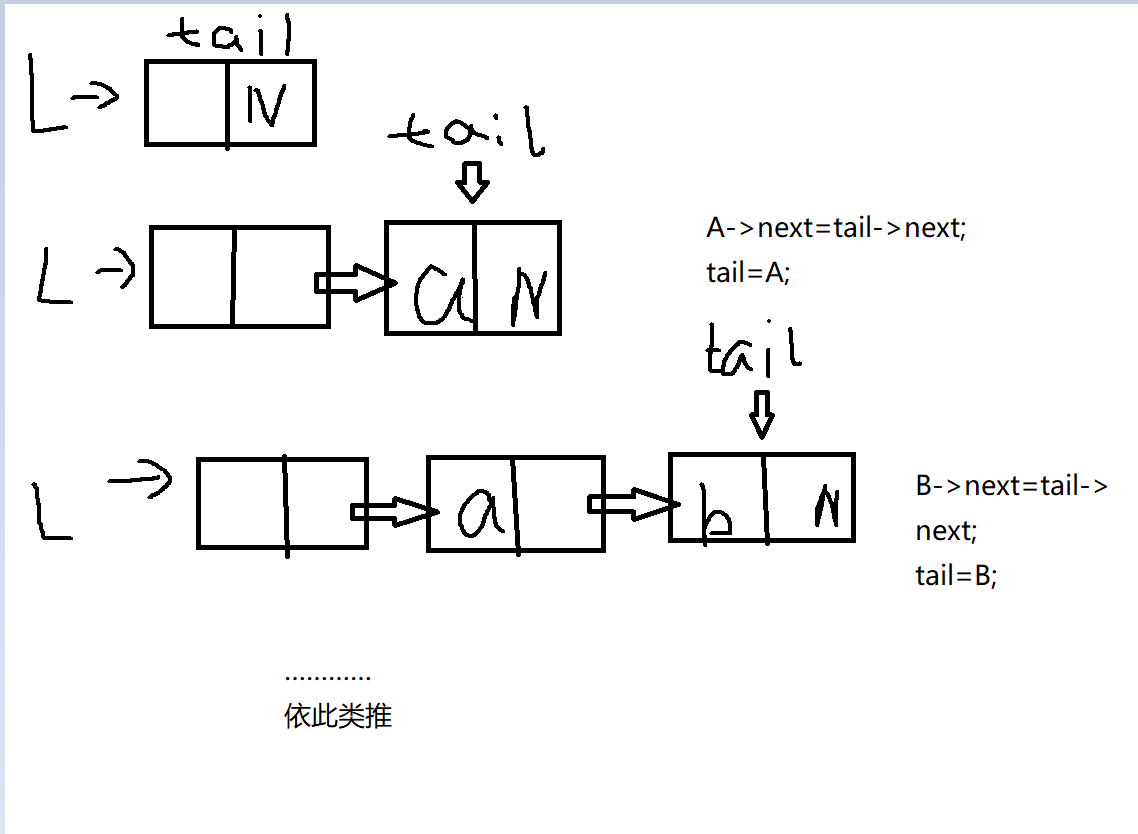
- 尾插法:即在插入节点时将节点插入到链表尾部,相比于头插法,尾插法多了一个尾指针用来定位链表末端。
- 主要代码及图解(pta 6-6):
for (i = 0; i < n; i++)
{
if ((p = new LNode) == NULL)
{
cout << "system error!";
exit(0);
}
cin >> data;
p->data = data;
p->next = NULL;
end->next = p;
end = p;
}
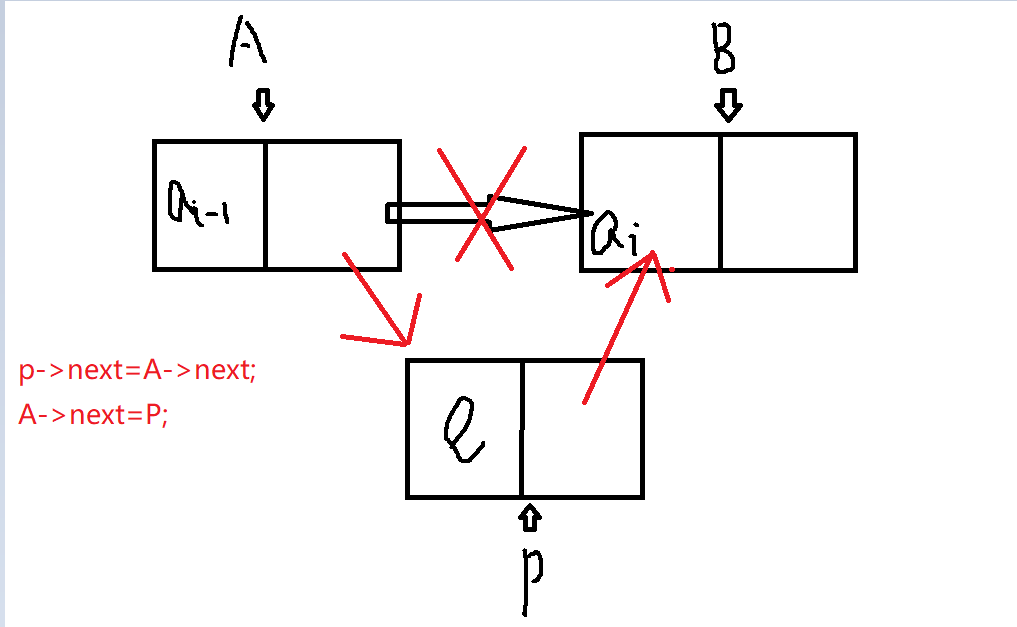
- 链表节点的插入:如果要使插入后链表仍然有序,则需要先找到插入位置,然后先保存前一个节点的后继关系,然后再改变,否则后续节点会丢失。如要插入到链表尾部,则需先遍历链表使指针定位到链表的最后一个节点,然后直接修改最后一个节点的后继关系即可。
- 主要代码及图解(pta 6-10):
while (curnode)
{
if (curnode->data >= e)
{
node->next = curnode;
prenode->next = node;
break;
}
if (curnode->next == NULL)
{
curnode->next = node;
break;
}
prenode = curnode;
curnode = curnode->next;
}
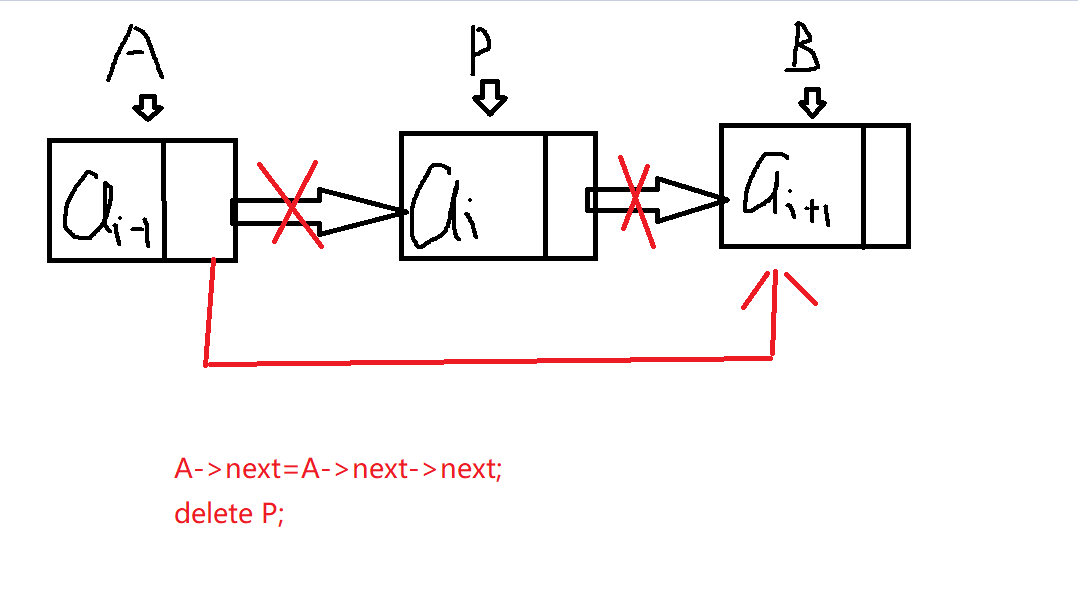
- 链表节点的删除:要删除一个节点之前,首先要保存该节点的后继关系,然后再删除该节点,否则会使后继节点的关系丢失。
- 主要代码及图解(pta-test 6-3):
while (L->next)
{
if (L->next->data >= min && L->next->data <= max)
{
temp = L->next;
L->next = L->next->next;
delete temp;
continue;
}
L = L->next;
}

- 有序表,尤其有序单链表数据插入、删除,有序表合并
- 有序单链表的数据插入:首先通过遍历链表来找到要插入的位置,然后先保存该位置的前一个节点的后继,再修改后继关系,否则同样会使后续节点的关系丢失。(做法与链表大致相同)
- 主要代码及图解(pta 6-10):
while (curnode)
{
if (curnode->data >= e)
{
node->next = curnode;
prenode->next = node;
break;
}
if (curnode->next == NULL)
{
curnode->next = node;
break;
}
prenode = curnode;
curnode = curnode->next;
}
}

- 有序表的数据删除:同样要先遍历链表找到要删除的数据的位置,然后先保存其后继,然后再删除,否则同样会使后续节点关系丢失。(做法与链表大致相同)
- 主要代码及图解():
while (curnode)
{
if (curnode->data == e)
{
if ((node = new LNode) == NULL)
{
cout << "system error!";
exit(0);
}
prenode->next = curnode->next;
node = curnode;
curnode = curnode->next;
delete node;
flag = 0;
continue;
}
prenode = curnode;
curnode=curnode->next;
}
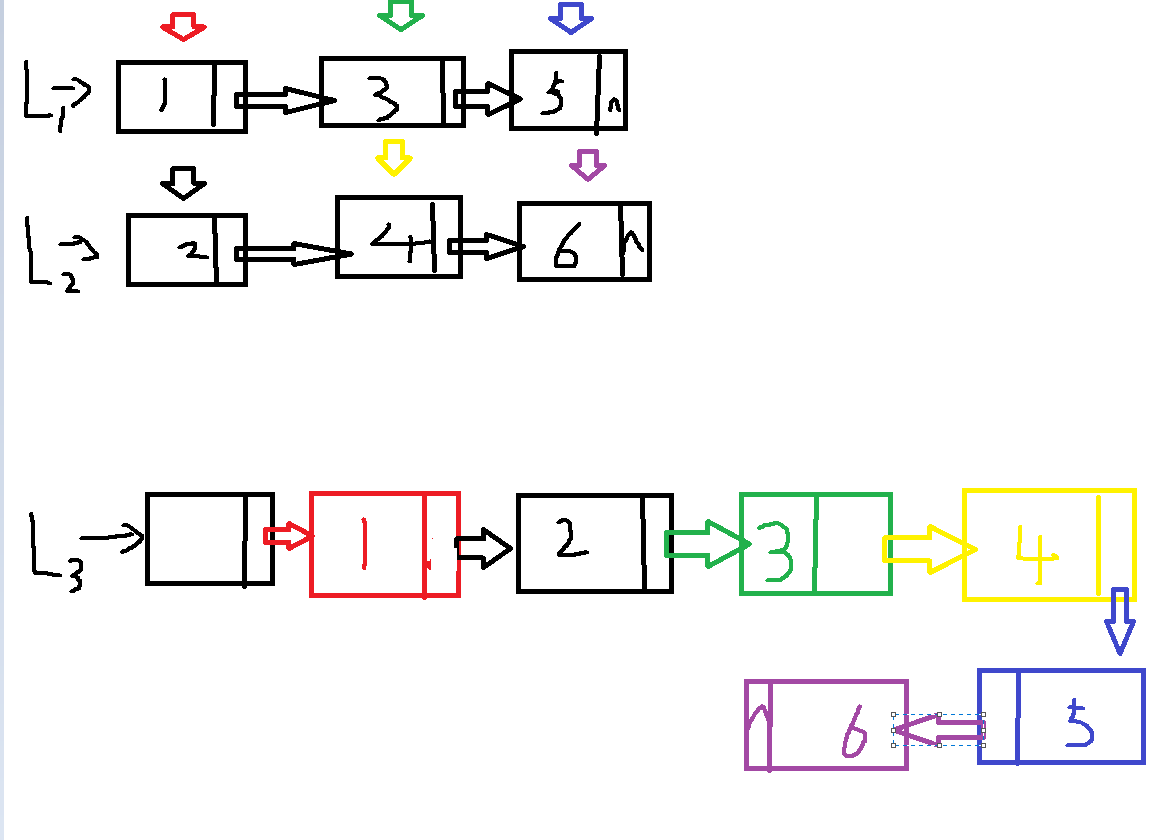
- 有序表的合并:可以采用二路归并法,即同时遍历两条链表,数据小的存入新链表,然后该链表和新链表的指针位置同时后移,另一条链表的指针位置不变。直到其中一条链表全部遍历完,然后将另一条链表剩下的节点依次插入新链表尾部。(二路归并法还可以用来找两个有序链表的中位数)
- 主要代码及图解(pta 6-9):
while (pa && pb)
{
if (pa->data < pb->data)
{
node = new LNode;
node->data = pa->data;
tail->next = node;
tail = node;
pa = pa->next;
}
else if (pa->data > pb->data)
{
node = new LNode;
node->data = pb->data;
tail->next = node;
tail = node;
pb = pb->next;
}
else
{
node = new LNode;
node->data = pa->data;
tail->next = node;
tail = node;
pa = pa->next;
pb = pb->next;
}
}
- 循环链表、双链表结构特点
-
循环链表结构特点:循环链表实际上可以看作一条单链表,但是这条单链表的最后一个节点的后继是指向头节点而不是
NULL。链表遍历完的判断条件不同于单链表的node->next==NULL,循环链表的空表判断条件是node->next==head。从循环链表的任一节点出发均可找到表中其他节点。

-
双链表结构特点:双链表其实也可以看作一条单链表,但是这条链表的结构体中除了后继指针还多了一个前驱指针。好处就是从链表的任意一个节点出发可以快速找到其前驱和后继节点,从任一节点出发可以访问其他节点。

-
1.2.谈谈你对线性表的认识及学习体会。
- 对线性表的认识:功能强大,相比于数组,虽然不如数组操作起来方便,但是比数组更节省空间,即建即插,不会像数组一样在不知道具体有多少个数据的情况下,要开辟大量空间,造成空间浪费;虽然线性表遍历起来麻烦,但是相比于数组在插入和删除时的多重循环,线性表只需要两三条语句即可完成,时间效率极高。
- 学习体会:在做线性表的相关题目时最容易出现的问题就是非法访问内存,因为不同于数组的遍历条件
a[i],不同题目的链表遍历条件可能不一样,有的是node->next,有的是node,需要看清题目要求,分情况使用,否则很容易出现非法访问内存;相比于数组,链表虽然操作起来方便,但是很容易出错,所以在做题目前需要先构思好大体思路。
2.PTA实验作业
2.1 6-9 jmu-ds-有序链表合并
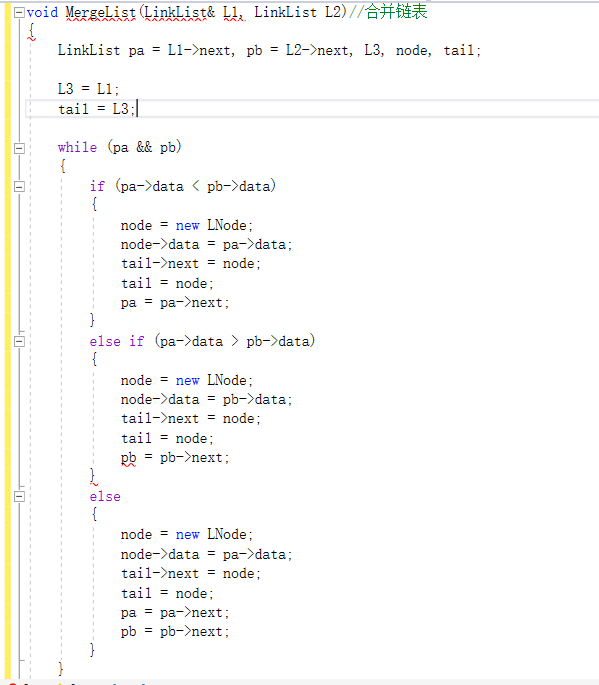
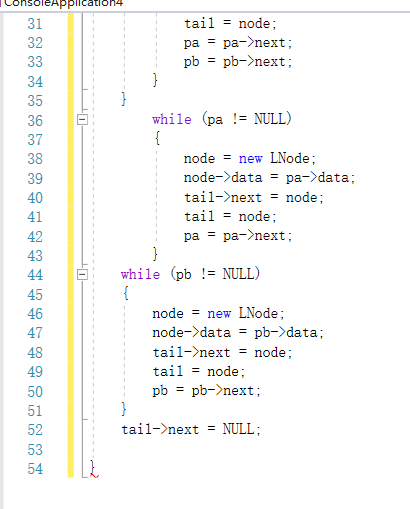
2.1.1 代码截图:
2.1.2 pta提交列表说明:

部分正确:一开始做的时候,循环条件用错了,用成了pa->next这种形式,导致有一条链表的最后一个节点没有正常插入,影响了后续节点的关系。
部分正确:修改完上一个错误后,还是部分正确,经反复检查,发现未遍历完的那条链表的剩余节点没有全部插入。原因在于我对剩余链表后续节点的处理方法只有一条语句:tail->next=node。后修改为while循环语句逐个插入。
完全正确:修改完上诉错误后提交通过。
2.2 7-1 两个有序序列的中位数
2.2.1 代码截图:
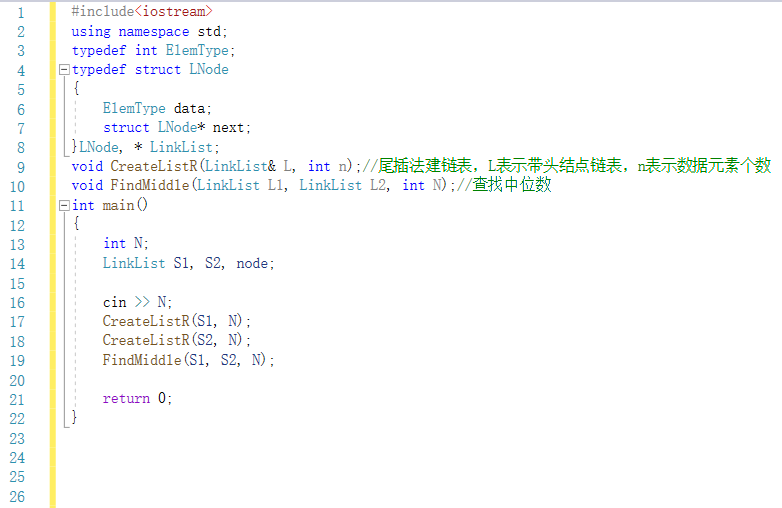

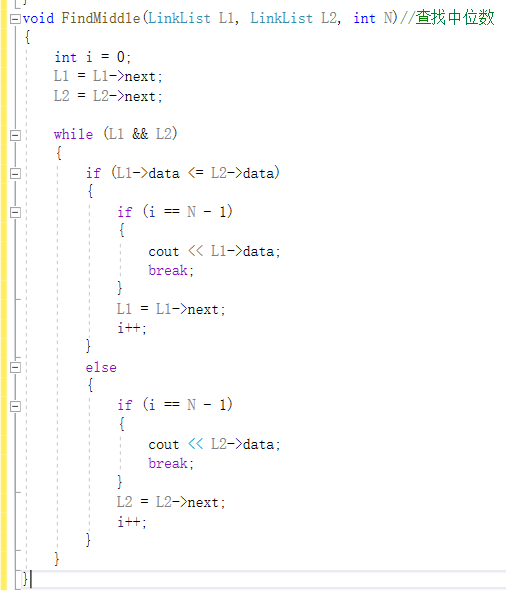
2.2.2 pta提交列表说明:
由于这题我先了解了相关做法,并且在VS上能成功运行后才提交到pta,没想到一次就过了。但是我在VS调试的时候还是遇到了一些问题的:
1.一开始同样是遍历条件出错,用成了L1->next&&L2->next,导致部分特殊情况下链表的最后一个节点无法遍历到。
2.还有就是对物理位置和实际位置的定义混淆,将中位数的判断条件写成i==N,导致找到的中位数出错,后修改为i==N-1后问题解决。
2.3 7-2 一元多项式的乘法与加法运算
2.3.1 代码截图:
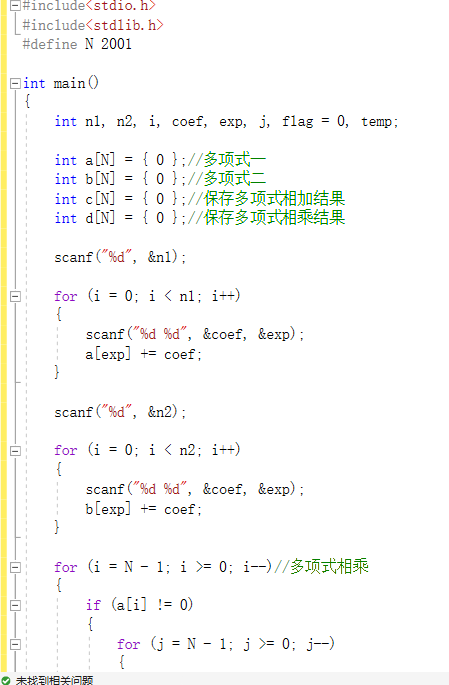


2.3.2 pta提交列表说明:
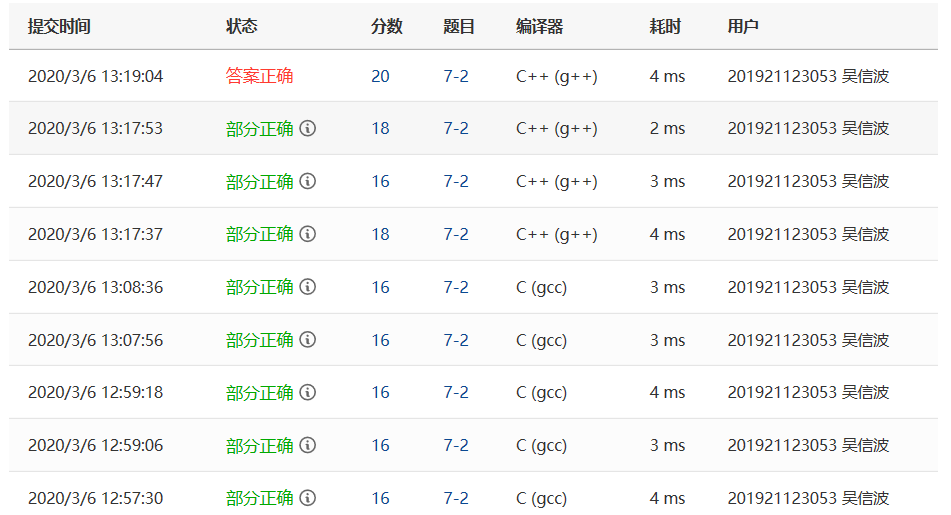
首先:
在看到这题时我的第一想法是用顺序表,但是在写代码的过程中发现用链表的方法来做这题的话时间复杂度非常的高,特别是在多项式相乘的代码上,还需要开辟新的节点,而且还得保证新的节点插入后链表要有序。于是果断放弃链表的做法,转用上学期学的哈希数组的做法,虽然空间复杂度比较高,但是时间复杂度相比于链表低了很多,而且操作起来也很方便。
部分正确1-5:在采用哈希数组的做法后,测试数据能通过了,但是提交到pta发现有两个测试点过不了,我反复检查后找不出错误,只好一个一个的带入数据检查,发现原来是我N的最大值出问题,题目要求是系数和指数做高1000,而相乘结果指数最高为2000,而我N的值设为1000,导致数据过大时分配的数组空间不够,测试点过不了。
部分正确6-8:发现上述错误后,我还是没有意识到N的值该设为多少,以为是数组的结束符还要占一个位置,于是将N改为1001,发现还是有一个测试点过不了。重新看了一遍题目后才发现问题所在。
答案正确:将N的值修改为2001后,提交通过。
3.阅读代码
3.1 题目及解题代码:


3.1.1 该题的设计思路:
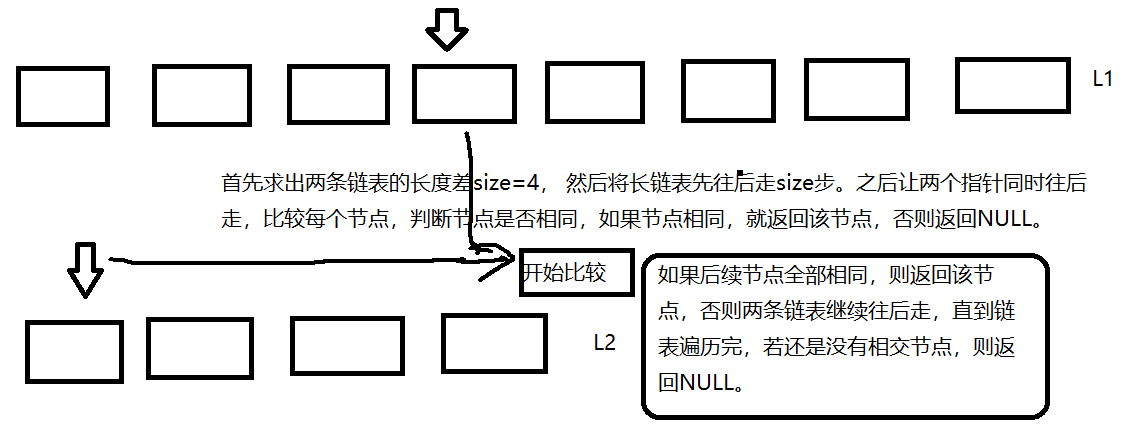
- 时间复杂度:T(n)=O(n)。
- 空间复杂度:S(n)=O(LA->length+LB->length)。
3.1.2 该题的伪代码:
while(遍历L1) 求出L1的长度; end while
while (遍历L2) 求出L2的长度; end while
求出两条链表的长度差size;
if(L1比L2长)
将L1先往后走size步;
while(同时遍历L1的剩余节点和L2)
如果L1->data==L2->data,return L1的当前位置节点;
end while
return NULL;
else
将L2先往后走size步;
while(同时遍历L2的剩余节点和L1)
如果L2->data==L1->data,return L2的当前位置节点;
end while
return NULL;
3.1.3 运行结果:
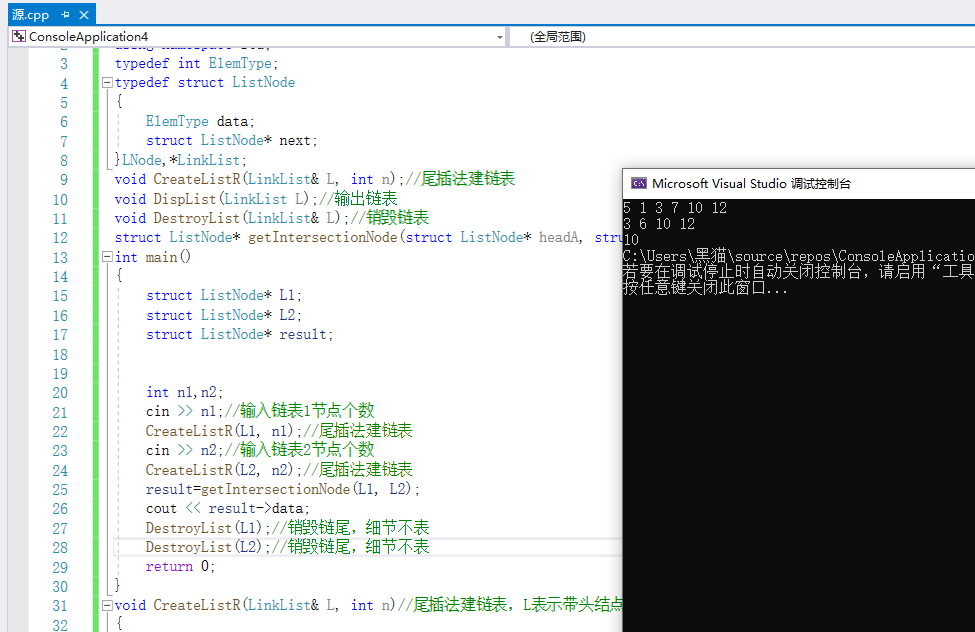
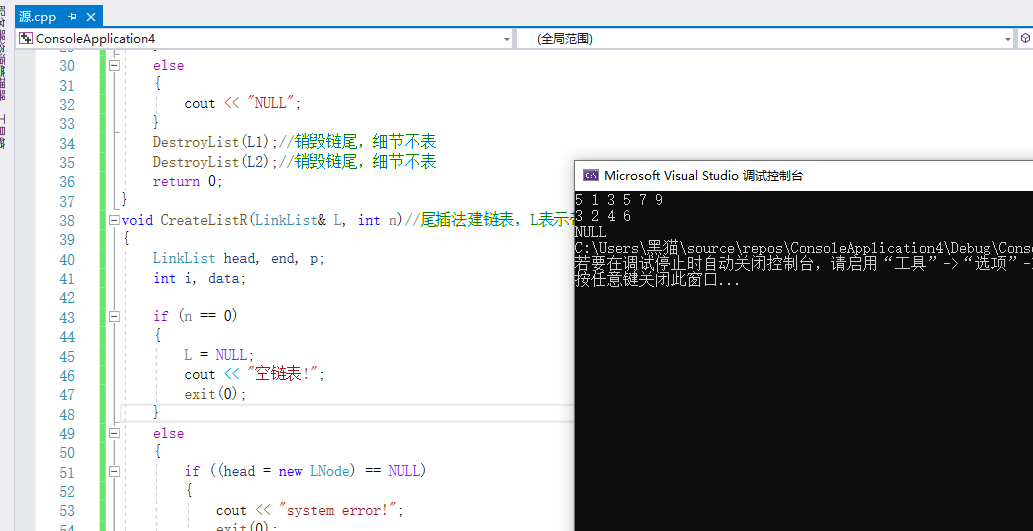
3.1.4分析该题目解题优势及难点
- 解题优势:该题解先将长链表往后走
size(即两条链表的长度差)个位置,而不是两条链表都从头开始比较,因为两条链表如果长度不一样的话,不可能从头开始就相交。这样做可以有效的节省时间,避免了不必要的比较。 - 难点:有可能会遇到当前位置两个链表节点相同,但是后续有个别节点不同,这种情况就得另外讨论解决,
属实麻烦。可以再从不相同的节点的后一个节点开始比较,如又遇到以上问题则再次循环,直到链表遍历完。
3.2 判断单链表是否回文解题代码:
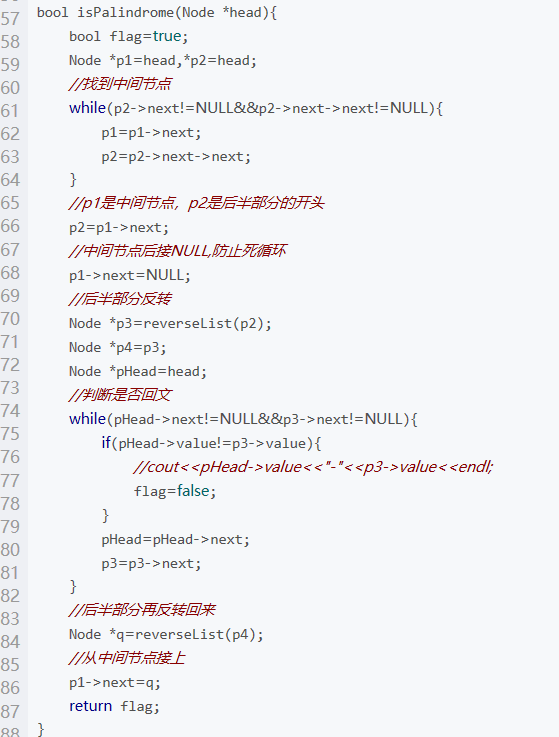
3.2.1 该题的设计思路:
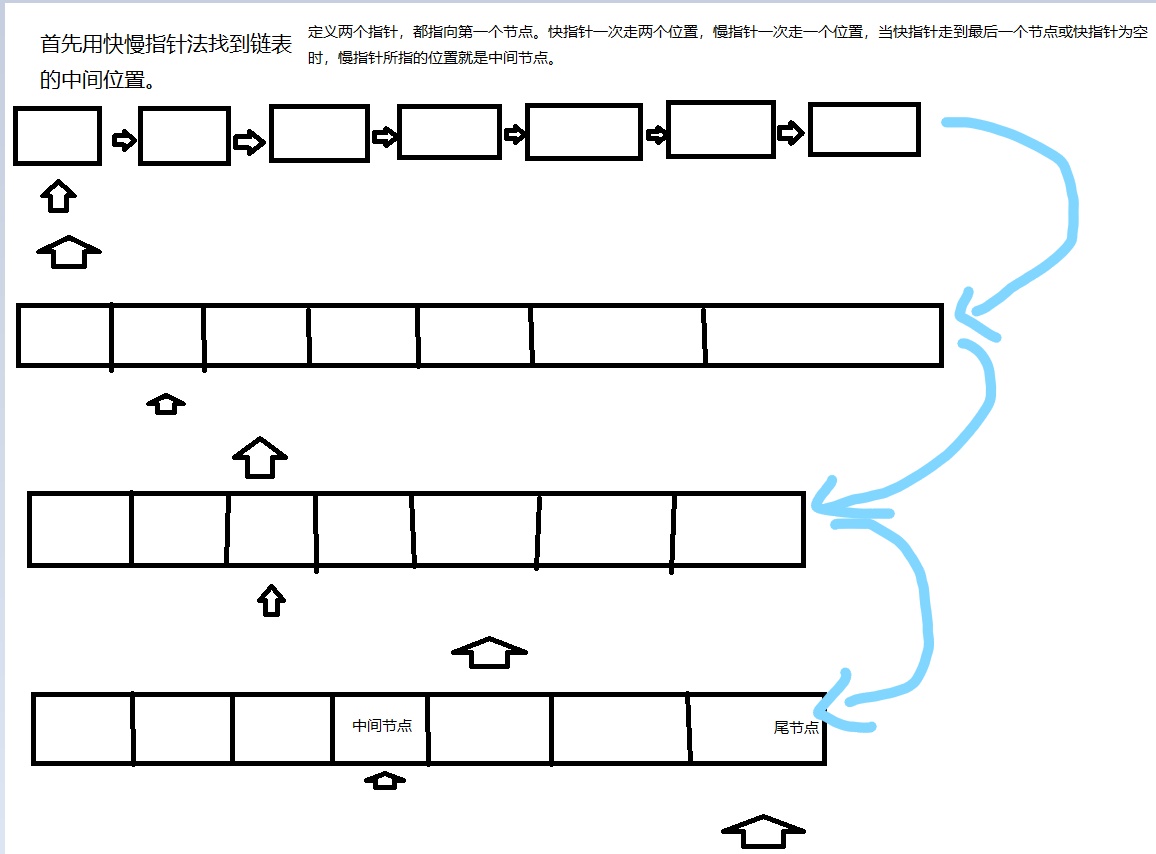
窄箭头是慢指针,宽箭头是快指针。

- 时间复杂度:T(N)=O(n)
- 空间复杂度:S(N)=O(n)
3.2.2 该题的伪代码:
定义初始状态flag=true;
定义两个指针,一个快指针,一个慢指针,均指向第一个节点;
while(快指针!=NULL&&快指针->next!=NULL)
快指针一次走两步,慢指针一次走一步;
end while
//慢指针即为链表的中间节点
以慢指针为分界线,将链表分割为前半部分和后半部分;
逆转后半部分链表;
while(同时遍历两个链表)
if(出现不相同的节点) 记录状态flag=false;
end while
将后半部分的链表逆转回来即恢复后半部分链表原本的顺序;
从中间节点将后半部分的链表接上;
return flag
3.2.3 运行结果:


3.2.4分析该题目解题优势及难点
- 解题优势:该题很有效的运用了
分割链表和逆转链表的做法来将一条单链表分割成前后两部分并将后半部分的链表逆转后与前半部分的链表对比。这样做就不需要单独去找链表的尾节点,可以节省时间提高效率。 - 难点:由于该题所给的结构体中不包含链表长度,所以无法直接找到链表的中间节点;而且该题所给链表为单链表,不是循环链表或双链表,无法直接定义到最后一个节点。