HDU1143 （递推）题解

Tri Tiling

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 4343    Accepted Submission(s): 2518

Problem Description

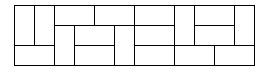
In how many ways can you tile a 3xn rectangle with 2x1 dominoes? Here is a sample tiling of a 3x12 rectangle.

 

Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30.

 

Output

For each test case, output one integer number giving the number of possible tilings.

 

Sample Input

2812-1

 

Sample Output

31532131

思路：

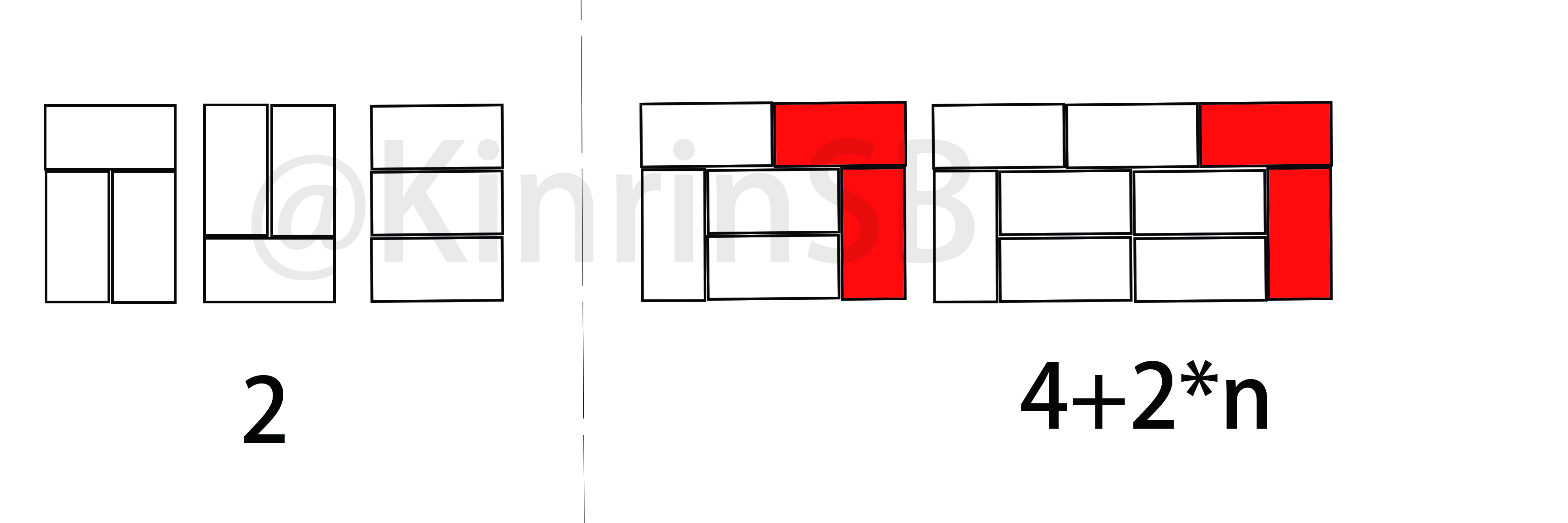
先来看能用来填满的格子的样式：1是只能加两列，2是能加4+2*n列

对第一种：f[n]=3*f[n-2]（在前n-2基础上不断加第一种）

对第二种：f[n]=2*f[n-4]+2*f[n-6]+...+2*f[0]（在第二种基础上加第一种方块）

两式相加：f[n]=3*f[n-2]+2*f[n-4]+2*f[n-6]+...+2*f[0]-----------1

由上式得出：f[n-2]=3*f[n-4]+2*f[n-6]+2*f[n-8]+...+2*f[0]------2

将2代入1式得出最后递归式：f[n]=4*f[n-2]-f[n-4]

Code:

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<cctype>
#include<queue>
#include<math.h>
#include<iostream>
#include<algorithm>
#define INF 0x3f3f3f3f
#define N 1000005
using namespace std;

int main(){
	int n;
	int a[35];
	a[0]=1,a[2]=3;
	for(int i=4;i<=30;i+=2) a[i]=4*a[i-2]-a[i-4];
	while(~scanf("%d",&n)){
		if(n==-1) break;
		if(n%2) printf("0
");
		else printf("%d
",a[n]);
	}
	return 0;
}