这里说几种处理字符串问题的常用方法
包括 哈希Hash,KMP,Trie字典树 和 AC自动机 四种

哈希 Hash
哈希算法是通过构造一个哈希函数,将一种数据转化为可用变量表示或者是可作数组下标的数
哈希函数转化得到的数值称之为哈希值
通过哈希算法可以实现快速匹配与查找
字符串 Hash
一般用于寻找一个字符串的匹配串出现的位置或次数
思考一下,如果我们要比较两个字符串是否相同,应该如何做
如果一个字符一个字符的对比,当两个字符串足够长时,时间代价太大
但是如果把每段字符串处理成一个数值,然后通过比较数值来确定是否相同,就可以做到 (O(1)) 实现这个操作
而处理每段字符串数值的函数,就是上面说的哈希函数
对于哈希函数的构造,通常选取两个数互质的 (Base) 和 (Mod) ((Base<Mod)),假设字符串 (S=s_1s_2s_3……s_n)
则我们可以定义哈希函数 (Hash(i)=(s_1 imes Base^{i-1} +s_2 imes Base^{i-2}+……+s_i imes Base^{0})mod Mod)
其中 (Hash(i)) 就是前 (i) 个字符的哈希值
然后,对于 (Base) 的次方我们也可以将它存储到一个数组 (Get[]) 中,使得 (Get[i]=Base^{i}),这样可以实现 (O(1)) 查询
(Tips:) 使用 unsigned long long 通过它的自然溢出,可以省去哈希函数中取模的一步
以上步骤的代码实现比较容易,如下:
Get[0]=1;
for(int i=1;i<=m;i++) Get[i]=Get[i-1]*base;
for(int i=1;i<=m;i++) val[i]=val[i-1]*b+(uLL)s1[i];
构造完哈希函数之后,要想求一个字符串某个区间内的哈希值怎么办
根据哈希函数的构造方式,不难想到,(Hash{l,r}=Hash(r)-Hash(l-1) imes Base^{r-l+1})
换成代码也就是这样:
inline int gethash(int l,int r){
int len=r-l+1;
return val[r]-val[l-1]*get[len];
}
哈希表
一种高效的数据结构,对于查找的效率几乎等同于常数时间,同时容易实现
比如说,要存储一个线性表 (A={k_1,k_2,k_3,k_4,……,k_n})
我们可以开一个一维数组,然后依次存储
但查找时会十分不便,当 (n) 足够大时,即使二分查找也仍需 (O(log n)) 的时间去查找某个元素
我们可以开一个数组 (B[n]),在存储时使得 (B[k_i]=k_i),可以将查找的时间降到 (O(1)),但是会造成极大的空间浪费
所以可以对此进行优化,使得 (B[k_i!!mod 13]),这样数组大小只需开到 (12) 即可
不过又会出现另一个问题,那就是会发生冲突,比如 (B[1]=B[14]=1)
因此我们考虑对数值相同的数记一个链表,查找时只查找对应的链表即可,时间复杂度取决于实际的链表长度,这就是哈希表
多产生的代价仅仅是消耗较多的内存,相当于用空间换取时间
另一方面,哈希函数也是决定哈希表查找速率的重要因素,因为只要哈希值分布足够均匀,查找的复杂度就会尽量小
对于哈希函数的构造,可以选择多种方法,比如除余法,乘积法,基数转换法等,只要尽量规避冲突都是可以的
为了规避不同的字符串出现相同的哈希值这种冲突,可以选择较大的模数,也可以构造多个哈希函数,比较当所有哈希值相同时才判定两个字符串相同
STL 库中的 (unordered\_map) 内部就相当于一个哈希表,其存储信息为无序的 (pair) 类型,插入速度较低,但查找速度更高,这里不多赘述
具体代码实现如下:
void init(){
tot=0;
while(top) adj[stk[top--]]=0;
}//初始化哈希表(多组数据时使用)
void insert(int key){
int h=key%b;//除余法
for(int e=adj[h];e;e=nxt[e])
if(num[e]==key) return;
if(!adj[h]) stk[++top]=h;
nxt[++top]=adj[h];adj[h]=tot;
num[tot]=key;
}//将一个数字 key 插入哈希表
bool query(int key){
int h=k%b;
for(int e=adj[h];e;e=nxt[e])
if(num[e]==key) return true;
return false;
}//查询数字 key 是否存在于哈希表中
注:因为我基本不写哈希表,所以此代码来自《信息学奥赛一本通提高篇》
KMP 算法
一种改进的字符串匹配算法,处理字符串匹配问题
由 D.E.Knuth,J.H.Morris 和 V.R.Pratt 同时发现,因此人们称它为克努特—莫里斯—普拉特操作,简称 KMP 算法
思考一下,如果我们要比较两个字符串,从而确定其中一个字符串是否为另一个的子串,应该怎么做
我们从两个字符串的第一个字符开始,逐个比较,当遇到不匹配的字符,就需重新匹配
如果从头开始重新匹配,可能前面许多字符已经完全相同,匹配过程时间代价较大
那我们可以根据匹配的字符串相同前后缀的长度来确定指针回溯位置
根据此原理,从上一个与当前字符相同的位置开始匹配,可以省掉许多无用的匹配过程,从而优化时间复杂度
这个操作的实现是通过处理出一个存储下一次从头匹配位置的数组 (Nxt[]),当某一位失配时,回溯到它对应的位置开始匹配,此位置之前的字符已确保完全相同
实例如图所示:

对于存储下一次从头匹配位置的数组的处理,可以根据递推来确定,就是用前面的值推出后面的值
在处理某一位的回溯数组时,考虑一下当前位置是否有可能由前一个位置的情况所包含的子串得到,也就是考虑一下是否 (Nxt[i]=Nxt[Nxt[i-1]]+1)
然后再造样例手玩一下就可以了
具体代码实现如下:
Nxt[1]=0;Fir=0;
for(int i=1;i<m;i++){
while(Fir>0&&s2[Fir+1]!=s2[i+1]) Fir=Nxt[Fir];
if(s2[Fir+1]==s2[i+1]) ++Fir;
Nxt[i+1]=Fir;
}//处理 Nxt 数组
Fir=0;
for(int i=0;i<n;i++){
while(Fir>0&&s2[Fir+1]!=s1[i+1]) Fir=Nxt[Fir];
if(s2[Fir+1]==s1[i+1]) ++Fir;
if(Fir==m){ans++;Fir=Nxt[Fir];}
}//统计匹配个数
可以看到预处理 (Nxt[]) 和主程序很像,因为预处理其实也是一个匹配串自我匹配的过程
Trie字典树
踹树
字典树是一种像字典一样的树,可用于处理字符串出现或匹配问题
具体说,就是选定一个根节点,然后以每个字符作为一个转移状态连出一条边,形成一个树状结构
树上的节点本身无实际意义
而所谓转移状态,就是满足 当前所匹配字符与某一条边上的字符相同 且 当前处于这条边的始点时,可以转移到这条边的终点并匹配下一个字符
这也是自动机的原理:满足条件便可转移
自动机可以是单向的,也可以是双向的
通常题目会给定若干个模式串,每个模式串由若干个字符相同。建树时,就以这些模式串来建树
假设我们给定了三个模式串
3
abc
de
afg
要将其建成一棵字典树
具体的建树方法如下:
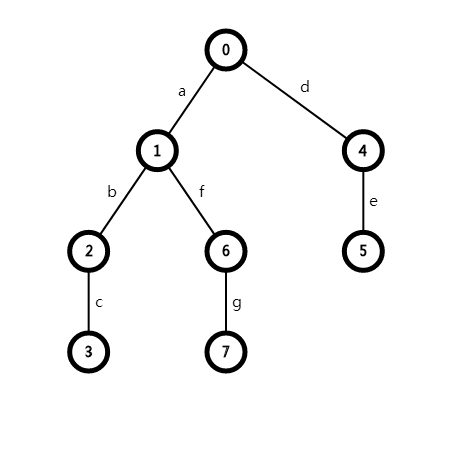
先看第一个模式串,由于树目前只有一个根节点,所以一路新建下去,从根节点到叶节点每条边的转移状态依次是abc的每个字符
再看第二个模式串,虽然树现在有了一条链,但是发现没有以d为转移状态的字符,因此另开一条链,也一路新建下去,方法同第一个模式串
最后看第三个模式串,发现有以a为转移状态的边,就沿此边向下遍历到 (1) 点,然后发现没有以f为转移状态的边,就从当前点另开一条链,一路新建下去
最后形成的字典树模型图如上图所示
建树过程中要维护的变量有 (Nxt[i][j]) 表示一条从节点 (i) 连出去的以 (j) 为转移状态的边,(Flag[i]) 标记以当前节点结尾的字符串是否存在
对于完成建树,或者说完成插入之后的操作,其实与插入操作差不多
要求出一个字符串是否存在于字典树中,就从根节点开始,每次找 转移状态与当前位置的字符相同的边遍历,若最后能找完就返回 (true),若中间失配则返回 (false)
若要求一个字符串在字典树中能找到的最末位置,只需多维护一个计数器,在遍历的同时统计,直到失配或者全部找完时再返回计数器的值就好了
具体代码实现如下:
struct Trie{
int Nxt[maxn][26],cnt;
bool flag[maxn];
void insert(char *s) {//插入字符串
int p=0,len=strlen(s+1);
for(int i=0;i<len;i++){
int c=s[i]-'a';
if (!Nxt[p][c]) Nxt[p][c]=++cnt;
p=Nxt[p][c];
}
flag[p] = 1;
}
bool find(char *s) {//查找字符串是否出现
int p=0,len=strlen(s+1);
for(int i=0;i<len;i++) {
int c=s[i]-'a';
if(!Nxt[p][c]) return 0;
p=Nxt[p][c];
}
return flag[p];
}
}Tri;
AC自动机
AC自动机,又叫 Aotumaton,是以自动机形式实现字符串查找匹配等其他操作的算法
因为个人感觉自己无法作出一个更加全面简介的概述了,所以在这里放一个 OI-Wiki 概述

用另一句话说,就是通过在 Trie字典树 上跑 KMP 来处理问题
失配指针
字面意思,就是一个在字符串失配时转移所用的指针 (Fail[]),类似与 KMP 的 (Nxt[])
KMP 的 (Nxt[]) 的原理以及处理方法上面都讲过了,这里就对比一下 (Fail[]) 与 (Nxt[])
(Nxt[]) 是在失配时回到前一个相同字符的位置,也就是它前面的的最长公共前后缀的结尾位置,但 (Fail[]) 是在失配时回到当前前缀状态可匹配的最长后缀状态的起始位置
因为 KMP 只对一个模式串做处理,而 AC自动机 是在字典树上运行,所以要处理多个模式串,所以 AC自动机 做匹配时,同一位置可能会匹配多个模式串
然后说明一下失配指针 (Fail[]) 该如何处理:
考虑字典树中当前的结点 (u),(u)的父结点是 (p),(p) 通过字符c的边指向 (u),即 (Nxt[p][c])。假设深度小于 (p) 的所有结点的 (Fail[]) 指针都已求得
- 如果 (Nxt[p][c]) 存在:则让 (u) 的 (Fail[]) 指针指向 (Nxt[Fail[p]][c])。相当于在 (p) 和 (Fail[p]) 后面加一个字符
c,分别对应 (u) 和 (Fail[u]) 。 - 如果 (Nxt[p][c]) 不存在:那么我们继续找到 (Nxt[Fail[Fail[p]]][c]) 。重复上一步的判断过程,一直跳 (Fail[]) 指针直到根结点。
- 如果真的没有,就让 (Fail) 指针指向根结点。
然后就处理完了 (Fail[]) 指针
我们可以简化它的过程,使得它的时间耗费降低,具体方法就是改变字典树的结构,使其成为字典图,方法如下:
- 如果 (Nxt[u][i]) 存在,我们就将它的的 (Fail[]) 指针赋值为 (Nxt[Fail[u]][i])
- 如果不存在,则令 (Nxt[u][i]) 指向 (Nxt[Fail[u]][i]) 的状态
显然,当在一个模式串后添加新字符时,我们会由原先模式串转移到新模式串的后缀,然后舍弃原模式串的部分前缀
因为上文说过 (Fail[]) 指针求的是最长后缀状态,与上面的显然结论相应
修改字典树结构后,尽管增加了许多转移关系,但结点所代表的字符串是不变的,所以这样处理可节省时间
构建与匹配
以上的处理步骤是出现在建树过程中的
建树,就是先将与根节点所连的点加入一个队列中 BFS,然后每次取出一个点处理对应的所有点的 (Fail[]) 指针
用代码实现就是这样:
void Build(){
for(int i=0;i<26;i++)
if(Nxt[0][i]) q.push(Nxt[0][i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(Nxt[u][i]) Fail[Nxt[u][i]]=Nxt[Fail[u]][i],q.push(Nxt[u][i]);
else Nxt[u][i]=Nxt[Fail[u]][i];
}
}
}
值得注意的是,入队的是根节点的儿子,而不是它本身,否则它儿子的 (Fail[]) 会标记成它本身
可以看出,建树过程实现了两个操作:构建失配指针和建立字典图
插入操作与 Trie字典树 里的插入无异,只需多统计一个出度,之后计数时会用到
对于计数操作,无非也是遍历,然后在存在出度的情况下加上它的出度并更改就完成了
此过程代码实现如下:
int Query(char *s){
int u=0,ans=0;
for(int i=1;s[i];i++){
u=Nxt[u][s[i]-'a'];
for(int j=u;j&&e[j]!=-1;j=Fail[j])
ans+=e[j],e[j]=-1;
}
return ans;
}
当然,具体要进行什么操作也要看实际情况,这种计数只是最简单的一种,有的也需要维护其他变量
最后,如果还不理解其中的某个过程,可以参考 OI-Wiki 对应文章里的例子,通过图示的方法进一步理解 Link
例题
Power Strings
Seek the Name, Seek the Fame
OKR-Periods of Words
A Horrible Poem
L语言
于是他错误的点名开始了
似乎在梦中见过的样子
AC自动机模板(简单)
AC自动机模板(加强)
写在最后
这四种知识点涵盖的内容其实远不止这些,还有一些更复杂的操作,比如 可持久化字典树、可持久化KMP 等等,由于本人能力问题就不写了
这篇文章是我花了三天多时间一点一点写出来的,是为了写给我和其他像我一样在这方面水平较低的人的,所以我修改了很多遍,但还是可能会有一些错误,还请多多包涵
至于这篇博客的名字,是同机房的某大佬替我想出来的,为了致敬同机房的另一个队爷(
希望这篇文章能让别人有收获吧