最短路和最小生成树应该是很早学的,大家一般都打得烂熟,总结一下几个问题
一 dijkstra
O((V+E)lgV) //V节点数 E边数
dijkstra不能用来求最长路,因为此时局部最优解已经不是全局最优解了(已知单源最短路的A点集在扩张的过程中依然满足最短路,而换成最长路则不满足)。
1.算法实现
dijkstra就是建立一个已知单源最短路的点集A,然后不断扩张这个点集。扩张的方法就是在未知最短路径的点集B中维护一个以目前的dis[x]排名(这个dis[x]是当前更新的最短路,不一定是最终结果)的优先队列,不断地将队首x加入A,然后用x来更新B。
2.正确性证明:
转自https://blog.csdn.net/softee/article/details/39034129,侵删
算法正确性证明
上一节描述的Dijkstra算法把图中的结点分为两个部分,分别标记为VISITED和UNVISITED,使用S和V-S来表示。为证明的方便,区分了S和V-S中的点的距离函数,分别为D和D_est,V-S中的距离函数被称为估值函数。算法的主要操作是循环执行第3到5步。证明算法的正确性,可以通过证明每次循环执行之前,S和V-S中的结点满足以下3条属性,执行之后依然满足。
属性1. S中任意m的点的的路径长度D[m]就是其最短路径。
属性2. 估值函数满足下述条件:
也就是说,对于V-S中的任意结点n,其估值路径D_est[n]是其只通过S中结点的最短路径。
属性3. V-S中估值最小的点n,D_est[n]的值就是其最短路径。
算法第一步S={s},只包含出发结点,且D[s]=0,故而满足属性1,更新相邻结点之后,容易证明,也满足属性2。属性3则需要证明,过程如下。
证明:假设D_est[n]不是n的最短路径,因为D_est是只通过S中结点的最短路径,所以结点n的真实的最短路径必然会经过集合S之外的结点,设路径上第一个非S中的点为j。则真实的最短路径的形式为s->...->j->...->n。因为假设了j之前的点都是S中的,所以根据属性2,D_est[j] < =D[n] < D_est[n],与n是估值最小的结点矛盾,所以属性成立。
算法接下来的操作是把n加入S,并试图更新V-S中结点的距离估值,容易证明,3-5步的一次操作之后,属性1-3仍然满足,所以得证。
这里我们可以知道,dijkstra维护的点集A是最短路的最优解,所以不能处理有负边权的图(可能会反过来使得A不再是最优解)。
3.堆优化的实现
引用自https://blog.csdn.net/geguojun/article/details/38260539,侵删
回想dijkstra算法中,for(1..v)的大循环内,每次在unknown的集合中找到dist[]数组里最小的那个,从unknown集合中删除该结点。朴素实现需要O(V)的时间,而用堆可以用O(log(V))的时间找到。然而,光找到还没完,找到之后要松弛所有与他相邻的unknown的结点(known的结点已经都是最短路了)。注意到如果要用堆实现优化,堆中存储的结点的priority值应当是图中该店当前的离source的距离。然而松弛操作会更新该距离,这就意味着我们要到堆内部找到这个结点的位置,更新距离,再维护堆。而堆是不提供检索功能的,找到一个结点需要O(V),完全糟蹋了O(log V)的优化了。更何况STL的priority_queue没有办法去接触内部的数据了。
其实,有一个可行的解决方案:一旦某个结点被更新了距离,一律但当成新结点加进堆里。这样会造成一个一个问题:一个图中的结点可能在堆中可能同时会存在好几个。但是这个不影响结果:先出堆的一定是距离最小的那个结点。其他的结点出堆的时候图里面的对应结点一定已经在known的集合了,到时候直接无视掉弹出来的已经known的结点,继续弹下一个,知道弹出一个unknown的结点为止。
这个做法最坏可能会让堆的高度加倍,然是任然不影响O(log n)的复杂度。不过具体的复杂度计算貌似不那么简单……不过实践证明速度确实有了很大提高,尤其是对于稀疏图。
打一个dijkstra+heap的模板//优先队列代替heap
1 #include<bits/stdc++.h> 2 using namespace std; 3 4 struct heapnode{ 5 int x,dis; 6 bool operator < (const heapnode & t) const{ 7 return t.dis < dis; 8 }; 9 }; 10 11 void ins(int x,int y,int d) 12 { 13 a[++al].x=x;a[al].y=y;a[al].d=d; 14 a[al].next=first[x];first[x]=al; 15 } 16 17 void dijsktra(int st) 18 { 19 priority_queue<heapnode> q; 20 for(int i=1;i<=n;i++) dis[i]=INF; 21 while(!q.empty()) q.pop(); 22 memset(done,0,sizeof(done)); 23 q.push(st);dis[st]=0;done[st]=1; 24 while(!q.empty()) 25 { 26 heapnode t=q.top();q.pop(); 27 int x=t.x,d=t.dis; 28 if(done[x]) continue; 29 done[x]=1; 30 for(int i=first[x];i;i=a[i].next) 31 { 32 int y=a[i].y; 33 if(dis[y] > dis[x]+a[i].d) 34 { 35 dis[y]=dis[x]+a[i].d; 36 q.push((heapnode){dis[y],y}); 37 } 38 } 39 } 40 } 41 42 int main() 43 { 44 freopen("a.in","r",stdin); 45 return 0; 46 }
1 struct node{ 2 int x,d; 3 node(int x,int d):x(x),d(d) {} 4 bool operator < (const node &t) const{ 5 return d > t.d; 6 } 7 }; 8 9 priority_queue<node> q; 10 11 void dijkstra(int st) 12 { 13 while(!q.empty()) q.pop(); 14 memset(in,0,sizeof(in));//in 是否在集合里 15 memset(dis,63,sizeof(dis)); 16 dis[st]=0; 17 q.push(node(st,0)); 18 19 while(!q.empty()) 20 { 21 node t=q.top();q.pop(); 22 int x=t.x,d=t.d; 23 if(in[x]) continue; 24 in[x]=1; 25 26 for(int i=first[x];i;i=a[i].next) 27 { 28 int y=a[i].y; 29 if(in[y]) continue; 30 if(dis[x]+a[i].d < dis[y]) 31 { 32 dis[y]=dis[x]+a[i].d; 33 q.push(node(y,dis[y]); 34 } 35 } 36 } 37 }
这种做法就保证了,比如下图 ,对于2 ,虽然一开始就找到了蓝色的这条路,但是最终会用橙色这条最短路。
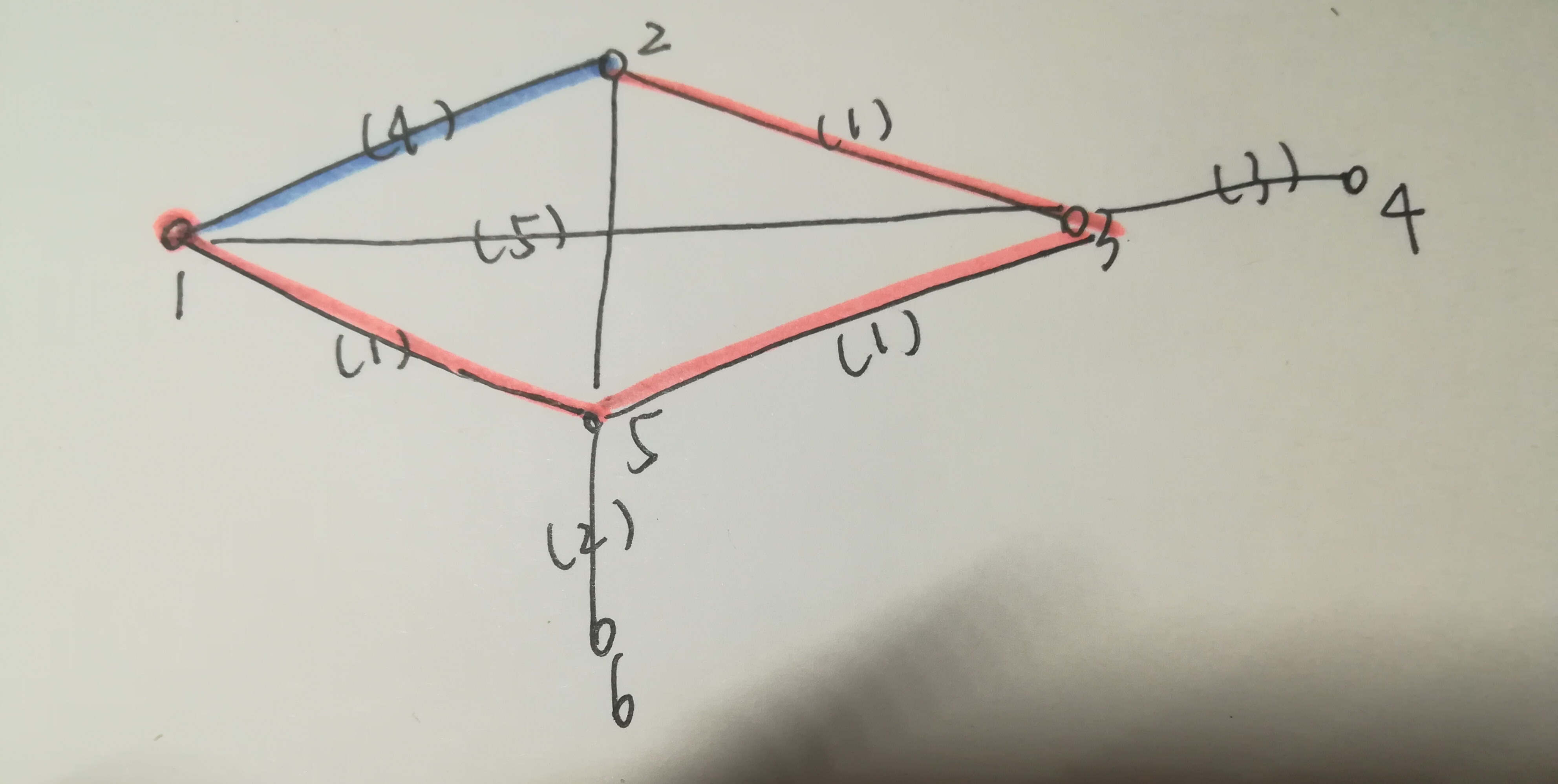
3.dijkstra+heap与spfa算法区别:
https://www.cnblogs.com/flipped/p/6830073.html
https://blog.csdn.net/gui951753/article/details/47863051
二 spfa
复杂度 O(ke),k<=2,最坏情况下是O(VE)
1.算法实现
spfa采用队列,每次队首出列进行松弛操作(不断动态逼近)来更新距离(队首之后还可以入队)。spfa可用于处理有负边权的图,如果一个点入队超过n次就是存在负环。
1 void spfa() 2 { 3 while(!q.empty()) q.pop(); 4 memset(in,0,sizeof(in)); 5 memset(dis,63,sizeof(dis)); 6 in[st]=0,dis[st]=0; 7 q.push(st); 8 while(!q.empty()) 9 { 10 int x=q.front();q.pop(); 11 for(int i=first[x];i;i=a[i].next) 12 { 13 int y=a[i].y; 14 if(dis[y] > dis[x]+a[i].d) 15 { 16 dis[y]=dis[x]+a[i].d; 17 if(!vis[y]) 18 { 19 vis[y]=1; 20 q.push(y); 21 } 22 } 23 } 24 vis[x]=0; 25 } 26 }
小结一下dijkstra与spfa
引用自https://www.cnblogs.com/flipped/p/6830073.html,侵删
复杂度分析对比
Dijkstra+heap
- 因为是堆,取队头需要O(lgV)。
- 松弛边时,因为点的d改变了,所以点v需要以新距离重新入堆,O(lgV),总共O(ElgV)。
- 因此总的是O((V+E)lgV)O((V+E)lgV)
SPFA
- 论文证明也不严格。复杂度不太好分析。
总的是O(kE)。k大概为2。- 复杂度应该是 O(VE)。
适用场景
如果是稠密图,Dijkstra+heap比SPFA快。稀疏图则SPFA更快。SPFA可以有SLF和LLL两种优化,SLF就是d比队头小就插入队头,否则插入队尾。
另外,Dijkstra和Prim也很相似,它们的区别主要是d的含义,前者是到s的临时最短距离,后者是到树的临时最短距离,相同点是,每次找d最小的更新其它点的距离。
三 prim
复杂度O(V^2)
1.算法实现
prim实质上是不断地再未加入最小生成树的点集B中,寻找一个距离已加入最小生成树的点集A最小的点,使其加入A中。
其实与dijsktra非常相似,区别就在于dijkstra中的dis是距离源点,而prim中是距离联盟(点集A)
模版
1 void prim() 2 { 3 memset(dis,63,sizeof(dis));//dis为到联盟的最短距离 4 memset(vis,0,sizeof(vis)); 5 dis[st]=0;vis[st]=1; 6 for(int i=1;i<n;i++)//除st外,一共还要找n-1个点 7 { 8 int mn=INF,id=0; 9 for(int j=1;j<=n;j++)//每次找到联盟最小的点 10 { 11 if(!vis[j] && dis[j]<mn) 12 { 13 mn=dis[j]; 14 id=j; 15 } 16 } 17 vis[id]=1; 18 for(int j=1;j<=n;j++) 19 { 20 if(!vis[j] && map[id][j]<dis[j]) 21 dis[j]=map[id][j]; 22 } 23 } 24 }
2.正确性证明
转自 https://www.cnblogs.com/sky-view/p/3250972.html,侵删
图p是一个连通图,Y是对p使用prim算法得到的一棵生成树,Y1是p的一棵最小生成树
1.若Y=Y1,显然prim算法是正确的
2.若Y≠Y1,可进行如下推导:
a)Y中有n(n≥1)条边不存在于Y1中,在构建Y的过程中,第一次遇到这样的一条边时(以e表示),则e的一个端点u落在V内(V是之前的prim运算得到的一个子顶点集),另一个端点v落在V外
b)Y1是连通的,故Y1中存在u到v的一条的路径,此路径上必然存在一条边f,它的一个端点落在V内,另一个端点落在V外
c)把e加入Y1,去掉f,Y1仍然连通,根据prim算法,权值W(f)≥W(e),否则e不会被选入V,如果W(f)>W(e),新构建的树的权值和会比Y1小,而Y1是最小生成树,因此W(f)>W(e)不成立,得W(f)=W(e)
d)对每一条类似e的边,重复过程c),最终Y和重新构建的的Y1拥有的边完全一致,新构建的Y1也是最小生成树,因此Y也是最小生成树,证明prim算法正确
四 kruskal
复杂度O(e)
1.算法实现
按边权排序,从小到大地选择两个端点一个在最小生成树点集另一个不在的边,直到V-1条为止。
这跟prim很不一样了,kruskal是把图划分为若干个联通分量再一点一点连起来的。
用到并查集来实现。
1 int findfa(int x) 2 { 3 if(fa[x]==x) return x; 4 fa[x]=findfa(fa[x]); 5 return fa[x]; 6 } 7 8 void kruskal() 9 { 10 sort(a+1,a+1+m,cmp); 11 for(int i=1;i<=n;i++) fa[i]=i; 12 int cnt=0; 13 for(int i=1;i<=m;i++) 14 { 15 a[i].tmp=0; 16 int x=a[i].x,y=a[i].y; 17 if(findfa(x)!=findfa(y)) 18 { 19 a[i].tmp=1; 20 cnt++; 21 fa[y]=x; 22 } 23 if(cnt==n-1) break; 24 } 25 }
2.正确性证明(有很多重要性质)
转自 https://blog.csdn.net/qq_36797743/article/details/70195715,侵删
首先,要先知道一个显而易见的东西:一个图的最小生成树方案不止一种,相信这个小学生都能理解
然后,有一个推论:对于图中任意一个点x,对于x点连出去的所有边,边权最小的一条至少存在于一棵最小生成树上。
对于这个推论的证明我想了一会,其实也不难。假设现在边(x,y),是x最短的一条,那么我们现在考虑将x,y连接起来(最小生成树的任意两点一定是连通的嘛),那么就只有两种不同的情况,直接连通和间接连通,我们现在就是要证明直接连通至少不比间接连通差。既然要间接连通,那么假设这条路是x——>a——>b.......——>y,其实这个最终连接的效果是可以等效于a——>b.......——>y——>x的,然而这里唯一的区别就是一个选择了了x——>a,一个选择了y——>x,那么我们知道选择(x,y)的代价肯定是不差于(x,a)的,证毕
有了这个推论后,你就可以大致体会到Prim算法的原理了,同时你也可以自己证明一个结论:对于任意一个图,他最小生成树中每种权值的边的数量是一定的(这是一个ACbzoj1016的重要结论,当然用的时候也是背的。。)
除此之外,我们就可以得到另外一个结论:如果某个连通图属于最小生成树,那么所有从外部连接到该图的边中的一条最短的边必然属于最小生成树。
这个结论也很好证明,就把之前的最小生成树看做一个点就好了。
于是我们就可以得到:当最小生成树被拆分成彼此独立的若干个连通分量的时候,所有能够连接任意两个连通分量的边中的一条最短边必然属于最小生成树。这个也是把每个连通分量看做一个点就好了。 也就是Kruskald的核心思想了!
然后我们再来探究一下最小生成树别的性质:
对于任意一个连通图,图中A点走到B点的所有路径中,最长的边最小值是肯定出现在最小生成树中A到B的路径上。
这个用Kruskal的做法来证明好了。首先在最小生成树上A——>B的路径肯定是唯一的,这个没毛病。就是说短的边会被先选上,所以最终使得A和B连通的最后一条边也是最短的,这也就保证了最长的边最短!!
这里证明一下一个无向图所有的最小生成树中某种权值的边的数目均相同这个性质:
引用自https://blog.csdn.net/wyfcyx_forever/article/details/40182739,侵删
我们证明以下定理:一个无向图所有的最小生成树中某种权值的边的数目均相同。
开始时,每个点单独构成一个集合。
首先只考虑权值最小的边,将它们全部添加进图中,并去掉环,由于是全部尝试添加,那么只要是用这种权值的边能够连通的点,最终就一定能在一个集合中。
那么不管添加的是哪些边,最终形成的集合数都是一定的,且集合的划分情况一定相同。那么真正添加的边数也是相同的。因为每添加一条边集合的数目便减少1.
那么权值第二小的边呢?我们将之间得到的集合每个集合都缩为一个点,那么权值第二小的边就变成了当前权值最小的边,也有上述的结论。
因此每个阶段,添加的边数都是相同的。我们以权值划分阶段,那么也就意味着某种权值的边的数目是完全相同的。
