最短路之 Dijkstra 算法

普通的 Dijkstra

这是一种运用贪心的单源最短路算法，就是求从一个节点出发，到任意一个点的最短距离
首先我们要一个图

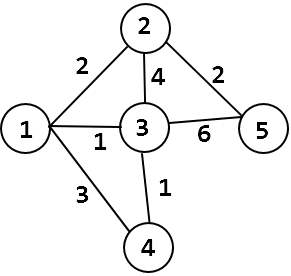
假设要求从 1 开始的单源最短路

dis[] 表示最短路数组， vis[] 表示当前节点是否被访问
那 Dijkstra 运用了贪心的思想，每次找到场上 dis 最小的且没被访问过的进行松弛操作。



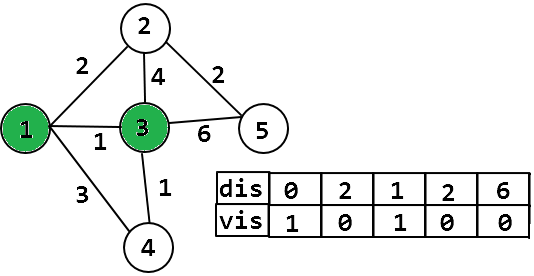
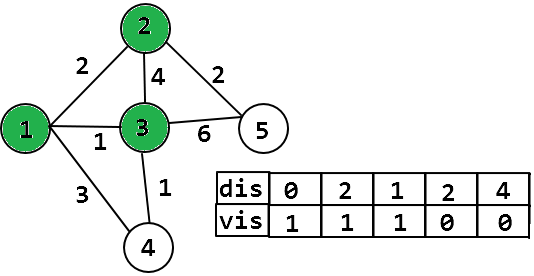
进行松弛操作的节点必须是没有被访问过的

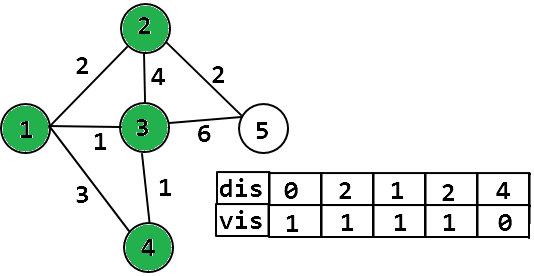
我们发现：更新 N-1 次后，剩下一个节点肯定不用更新了，所以只要 N-1 次更新。
算上找到最小值，和松弛操作，复杂度为(O(n^2))。
由于代码实现简单懒，这里就不给出了。

注： Dijkstra 无法运行于负权图或求最长路（最长路贪心是错的）

优化

发现 N-1 次更新是必须的，但是找最大值可以是不是可以用数据结构优化呢？
答案是肯定的，用一个树形结构维护顶端的最小值下标

zkw 线段树优化

感谢一位 Luogu 大佬的思路！

#include<bits/stdc++.h>
#define rg register int
using namespace std;
const int inf=-1u>>1,N=100005,M=200005;
int lst[M],nxt[M],to[M],w[M],dis[N],n,m,s,fr;
namespace zkw{
	int tr[N<<2],sgt=1;
	inline void build(rg n){while(sgt<=n)sgt<<=1;--sgt;tr[0]=N-1;}
	inline void clr(){for(rg i=1;i<=(sgt<<1)+1;i++)tr[i]=0;}
	inline int cmp(const rg&x,const rg&y){return dis[x]<dis[y]?x:y;}
	inline void Mdy(rg x,rg w){for(rg i=x+sgt;dis[tr[i]]>w;i>>=1)tr[i]=x;dis[x]=w;}
	inline void del(rg x){tr[x+=sgt]=0;x>>=1;while(x)tr[x]=cmp(tr[x<<1],tr[x<<1|1]),x>>=1;}
}
using namespace zkw;
inline void dijkstra(rg s,rg*dis){
	for(rg i=0;i<=n;i++) dis[i]=inf;clr();Mdy(s,0);
	for(rg T=1;T<=n;T++){
		rg u=tr[1];del(u);
		for(rg i=lst[u];i;i=nxt[i])
			if(dis[to[i]]>dis[u]+w[i])
				Mdy(to[i],dis[u]+w[i]);
	}
}
int main(){
	scanf("%d%d%d",&n,&m,&s);build(n);
	for(rg i=1;i<=m;i++){
		scanf("%d%d%d",&fr,&to[i],&w[i]);
		nxt[i]=lst[fr],lst[fr]=i;
	}
	dijkstra(s,dis);
	for(rg i=1;i<=n;i++) printf("%d ",dis[i]);
}

或者用二叉堆优化

#include<bits/stdc++.h>
using namespace std;
const int N=100005,M=200005;
struct node {
	int v,id;
	node(int x,int y):v(x),id(y) {}
	bool operator<(node x) const
	{ return v>x.v; }
};
priority_queue<node> q;
int n,m,s,vis[N],dis[N],lst[N],nxt[M],to[M],qz[M];
inline void Dijkstra() {
	memset(dis,100,sizeof(dis));
	dis[s]=0;
	q.push(node(0,s));
	for(int u;!q.empty();) {
		u=q.top().id,q.pop();
		if(vis[u])continue; vis[u]=1;
		for(int i=lst[u],v;i;i=nxt[i])
			if(dis[v=to[i]]>dis[u]+qz[i]) {
				dis[v]=dis[u]+qz[i];
				q.push(node(dis[v],v));
			}
	}
}
int main() {
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1,fr;i<=m;i++) {
		scanf("%d%d%d",&fr,&to[i],&qz[i]);
		nxt[i]=lst[fr],lst[fr]=i;
	}
	Dijkstra();
	for(int i=1;i<=n;i++)printf("%d ",dis[i]);
}

(P.S) zkw 版本是本蒟蒻半年前写的，与现在的码风差别很大，
OI 一生就一次，且珍惜罢了