【BZOJ 1478】 1478: Sgu282 Isomorphism （置换、burnside引理）

1478: Sgu282 Isomorphism

Description

给 定一个N 个结点的无向完全图（ 任意两个结点之间有一条边）， 现在你可以用 M 种颜色对这个图的每条边进行染色，每条边必须染一种颜色。 若两个已染色的图，其中一个图可以通过结点重新编号而与另一个图完全相同， 就称这两个染色方案相同。 现在问你有多少种本质不同的染色方法，输出结果 mod P。P 是一个大于N 的质数。

Input

仅一行包含三个数，N、M、P。

Output

仅一行，为染色方法数 mod P 的结果。

Sample Input

3 4 97

Sample Output

20

HINT

数据范围：1≤N≤53，1≤M≤1000，N

【分析】

　　关于这题，这文档讲得很清楚：http://wenku.baidu.com/view/fee9e9b9bceb19e8b8f6ba7a.html?from=search###

　　这题想起来挺难的。

　　首先它是对点的置换，但是是边染上了颜色，就是说实际上是边的置换。所以我们要看一下点置换和边置换之间的关系。

　　假定一个点置换，把它表示为循环，比如是(a1,a2,....)(b1,b2...)(c1,c2...)...

　　1、对于不在一个循环里面的点：

　　比如a1,b1, 那么会有边循环((a1,b1),(a2,b2)...) 设a循环的循环节是l1,b循环的循环节是l2,那么形成的边循环的循环节显然是LCM(l1,l2)。

　　一共有l1*l2个点对，每个点对都在一个循环节为LCM(l1,l2)的循环上，所以一共有l1*l2/LCM(l1,l2)=GCD(l1,l2)个循环节，所以C(f)=m^GCD(l1,l2)。（回到burnside引理，C为置换之后仍为本身的数目，就是说要循环节里的每条边都一样的颜色）

　　2、对于在一个循环里面的点：

　　比如a1、a2。设这个a循环的循环节为l1。

　　如果l1是奇数，那么循环长度为l1，一共有C(l1,2)个点对，所以是(l1-1)/2个循环节，所以C(f)=m^((l1-1)/2)。

　　如果l1是偶数，除了上面这种情况之外，还有一种的循环节是l1/2（就是两个点刚好相隔半个周期，而边是双向的），所以一共有(C(l1,2)-l1/2)/l1+1=l1/2个点对。

　　整理一下：

　　

　　

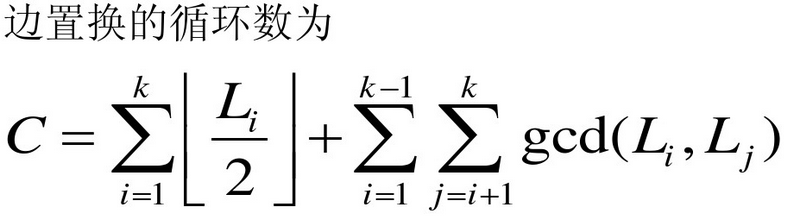
　　所以代码很简单，只要枚举n的拆分，然后计算不动点就好了。这里有用到逆元，p是质数可以用费马小定理。

　　分母上面先乘完再求逆元，我就是一边乘一边逆元就超时了。。。ORZ。。。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define Maxn 60
#define LL long long

int n,m;
LL pw[Maxn],N,p,ans;

LL qpow(LL a,LL b)
{
    LL ans=1;
    while(b)
    {
        if(b&1) ans=(ans*a)%p;
        a=(a*a)%p;
        b>>=1;
    }
    return ans;
}

LL l[Maxn];

int gcd(int a,int b)
{
    if(b==0) return a;
    return gcd(b,a%b);
}

void get_ans(int x)
{
    int c=0;
    for(int i=1;i<=x;i++) c+=l[i]/2;
    for(int i=1;i<=x;i++)
     for(int j=i+1;j<=x;j++) c+=gcd(l[i],l[j]);
    LL now=1;
    for(int i=1;i<=x;i++) now=(now*l[i])%p;
    int cnt=1;
    for(int i=2;i<=x;i++)
    {
        if(l[i]!=l[i-1])
        {
            now=(now*pw[cnt])%p;
            cnt=0;
        }
        cnt++;
    }
    now=(now*pw[cnt])%p;
    now=(N*qpow(now,p-2))%p;
    ans=(ans+now*qpow(m,c))%p;
    // printf("%d
",ans);
}

void ffind(int x,int st,int h)
{
    if(h==0)
    {
        get_ans(x-1);
    }
    if(h<st) return;
    for(int i=st;i<=h;i++)
    {
        l[x]=i;
        ffind(x+1,i,h-i);
    }
}

int main()
{
    scanf("%d%d%lld",&n,&m,&p);
    N=1;
    for(int i=1;i<=n;i++) N=(N*i)%p;
    pw[0]=1;
    for(int i=1;i<=n;i++) pw[i]=(pw[i-1]*i)%p;
    ans=0;
    ffind(1,1,n);
    printf("%lld
",(ans*qpow(N,p-2))%p);
    return 0;
}

2017-01-12 11:34:31