《剑指Offer》+ 牛客网
问题:大家都知道斐波那契数列(1,1,2,3,5,8,13...),现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。
n<=39
1. 递归
public class Solution { public int Fibonacci(int n) { if (n < 0) { return -1; } else if (n == 0) { return 0; } else if (n < 3) { return 1; } else { return Fibonacci(n - 1) + Fibonacci(n - 2); } } }
2. 改进版,相较于递归减少了许多重复计算,有一些技巧性
public class Solution { public int Fibonacci(int n) { if (n <= 0) { return 0; } else if (n < 3) { return 1; } else { int first = 1; int second = 1; int result = 0; for (int i = 3; i <= n; i++) { result = first + second; first = second; second = result; } return result; } } }
3. 动态规划
public class Solution { private int results[] = new int[40]; public int Fibonacci(int n) { if (n <= 0) { return n; } else if (results[n] > 0) { return results[n]; } else if (n < 3) { results[n] = 1; return results[n]; } else { results[n] = Fibonacci(n - 1) + Fibonacci(n - 2); return results[n]; } } public static void main(String[] args) { System.out.println(new Solution().Fibonacci(39)); } }
题目描述
青蛙跳台阶问题:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
不难看出其实就是斐波那契数列的变形。
题目描述
变态跳台阶:一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
数学归纳法,就是2的n-1次方
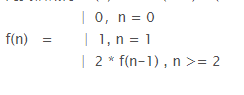 ,所以f(n) = f(1) * 2n-1 = 2n-1
,所以f(n) = f(1) * 2n-1 = 2n-1public class Solution { public int JumpFloorII(int target) { return 1 << (target - 1); } }