树链剖分讲解

树链剖分___步骤

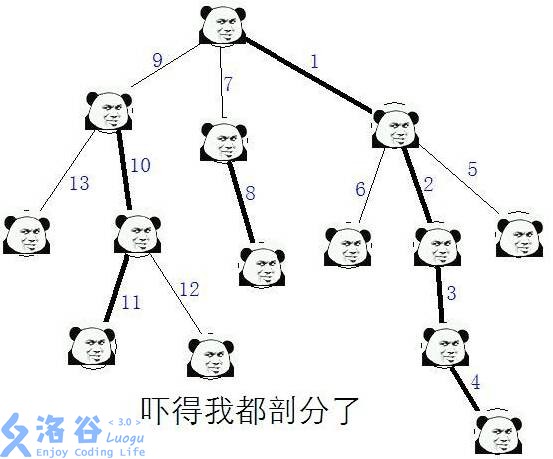
一.按照dfs序 将点重新标号.

　　首先,我们要理解,为什么一定要按dfs序来标号,因为,树链剖分要操作的是一棵树上,改变两个点之间最小路上边的数据,主要是因为,每一条找到的最短路,他们点的dfs序,都可以拆成几段连续的数值,所以我们可以联想到线段树,当然这是后面的步骤;每一条最短路既然都可以用这个dfs序来分解,所以就用dfs序来给点重新编号,这里用一个id数组,表示用dfs标号后的每个点的位置.

　　然后就可以对它这棵树,剖分成几条链.所以进行下一步操作.

 

 

二.按照重新标号后的编号,再继续将整棵树剖分成若干条链.

　　其实,在dfs序之后,就可以对整棵树变成,几条单链,也就可以对任意的两个点之间的最短路进行组合,也就是剖分组合.

　　 然后就可以引入几个量:

　　重儿子,重边,重链,链顶

　　然后就又是一遍dfs,带上的参数,为当前的链顶和当前所到的点.然后对它进行拆解.拆解之后,每个点都属于一条链,然后对于之后每个点的操作就会有很大的用处.

 

三.插入操作

　   插入操作的话首先有两个点和要修改的值,所以先输入两个点.

　　然后,我们第一步首先是把两个点的分别属于哪一条链找出来.如果两个点不在同一条链上的话,那么,我们就直接将当前这两个点的链顶里面较小的那个往上跳,同时在线段树里面,对已经跳完的这条链进行修改.然后再将这个点跳到链顶的父亲节点上面来.再进行递归操作,当两个点的链顶已经一样时j就可以进行下一步操作,继续找两个点的链顶,当已经为同一条链时,则直接在线段树里面对这两个点之间的这一段区间进行修改.

　　总体上来说,大概的思路就是通过链的分解把本来繁琐的找LCA的过程变成了几条链.然后数值是在线段树上修改,这样的话也就可以实现普通修改做不到的整条路一遍修改.时间复杂度大概是把O(n)优化成了O(klogn),k一般是小于10的,也就达到了对整棵树的操作.

 

四.查询操作

　　查询和插入其实感觉差不多,也都是先找到要查询的几段区间,然后再是线段树的常规操作.

五.小结

　　我们用树链剖分,其实就是为了把树上的一些链直接用数据结构进行维护,然后就可以达到降低时间复杂度的效果.也可以做一些普通的树直接用LCA倍增进行修改的方法,也就有了优化.

 

代码:

　　洛谷 P3384 树剖模板

         

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<cmath>
#define ll long long
#define llk(x) (x*2)
#define rrk(x) (x*2+1)
using namespace std;
const int maxn=500008;

ll n,m,s,p;

ll read()
{
    char ch=getchar();ll f=1,w=0;
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch<='9'&&ch>='0'){w=w*10+ch-'0';ch=getchar();}
    return f*w;
}

struct sj{
    int to;
    int next;
}a[maxn*2];
ll head[maxn],size;
ll val[maxn],ass[maxn];
ll id[maxn],pos[maxn];                    //id为位置 pos为线段树中的位置
ll top[maxn],fa[maxn];
ll son[maxn],dep[maxn];

void add(ll x,ll y)
{
    a[++size].to=y;
    a[size].next=head[x];
    head[x]=size;
}

ll num[maxn];
void dfs(ll rt,ll pre,ll deeep)
{
    num[rt]=1;
    fa[rt]=pre;
    dep[rt]=deeep;
    for(ll i=head[rt];i;i=a[i].next)
    {
        ll tt=a[i].to;
        //dep[tt]=deeep;
        if(tt!=pre)
        {
        dfs(tt,rt,deeep+1);
        num[rt]+=num[tt];
        if(num[tt]>num[son[rt]])
        son[rt]=tt;
        }
    }
    return;
}

ll dfn=0;
void dfs_Found(ll rt,ll zu)
{
    dfn++;
    id[rt]=dfn;val[dfn]=ass[rt];
    if(son[rt]!=-1)
    {
        top[rt]=zu;
        dfs_Found(son[rt],zu);
    }
    else
    {
        top[rt]=zu;
        return;
    }
    for(int i=head[rt];i;i=a[i].next)
    {
        ll tt=a[i].to;
        if(tt!=son[rt]&&tt!=fa[rt])
        dfs_Found(tt,tt);
    }
    return;
}

long long lazy[500004],sgm[500005];

void build(ll node,ll left,ll right)
{
      if(left==right){
      sgm[node]=val[left];
      return;
    }
    if(left>right)
    return;
    ll dist=(left+right)/2;
    build(llk(node),left,dist);
    build(rrk(node),dist+1,right);
    sgm[node]=sgm[llk(node)]+sgm[rrk(node)];
    return;
}

void push_down(ll node,ll l,ll r)
{
    ll dist=(l+r)/2;
    sgm[llk(node)]+=lazy[node]*(dist-l+1);
    sgm[rrk(node)]+=lazy[node]*(r-dist);
    lazy[llk(node)]+=lazy[node];
    lazy[rrk(node)]+=lazy[node];
    lazy[node]=0;
}

void insert(ll node,ll left,ll right,ll l,ll r,ll v)                       
{
    if(left>r||right<l)
    return;
    if(left>=l&&right<=r)
    {
      sgm[node]+=v*(right-left+1);
      lazy[node]+=v;
      return;
    }
    push_down(node,left,right);
      ll dist=(right+left)/2;
    insert(llk(node),left,dist,l,r,v);
    insert(rrk(node),dist+1,right,l,r,v);
    sgm[node]=sgm[llk(node)]+sgm[rrk(node)];
    return;
}

long long check(ll node,ll left,ll right,ll l,ll r)
{
    if(l>right||r<left)
    return 0;
    if(right<=r&&left>=l)
    return sgm[node];
    push_down(node,left,right);
    ll dist=(left+right)/2;
    return check(llk(node),left,dist,l,r)+check(rrk(node),dist+1,right,l,r);    
}

ll getsum(ll x,ll y)
{
    ll rest=0;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])
        swap(x,y);
        rest+=check(1,1,n,id[top[x]],id[x]);
        x=fa[top[x]];
    }
    if(id[x]>id[y])
    swap(x,y);
    rest+=check(1,1,n,id[x],id[y]);
    return rest;
}

void change(ll x,ll y,ll v)
{
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])
        swap(x,y);
        insert(1,1,n,id[top[x]],id[x],v);
        x=fa[top[x]];
    }
    if(id[x]>id[y])
    swap(x,y);
    insert(1,1,n,id[x],id[y],v);
    return;
}

int main()
{
    memset(sgm,-1,sizeof(sgm));
    n=read();
    m=read();
    s=read();
    p=read();
    for(int i=1;i<=n;i++)
    ass[i]=read();
    for(int i=1;i<n;i++)
    {
        int x,y;
        x=read();
        y=read();
        add(x,y);
        add(y,x);
    }
    memset(son,-1,sizeof(son));
    dfs(s,0,1);
    dfs_Found(s,s);
    build(1,1,n);
    for(int i=1;i<=m;i++)
    {
        ll pd,x,y,z;
        ll ans;
        pd=read();
        if(pd==1)
        {
            x=read();
            y=read();
            z=read();
            change(x,y,z);
            continue;
        }
        if(pd==2)
        {
            x=read();
            y=read();
            ans=getsum(x,y);
            cout<<(ans%p)<<endl;
            continue;
        }
        if(pd==3)
        {
            x=read();     
            y=read();
            insert(1,1,n,id[x],id[x]+num[x]-1,y);
            continue;
        }
        if(pd==4)
        {
            x=read();
            ans=check(1,1,n,id[x],id[x]+num[x]-1);
            cout<<(ans%p)<<endl;
            continue;
        }
    }
    return 0;
}