题目描述
地平线(x轴)上有n个矩(lou)形(fang),用三个整数h[i],l[i],r[i]来表示第i个矩形:矩形左下角为(l[i],0),右上角为(r[i],h[i])。地平线高度为0。在轮廓线长度最小的前提下,从左到右输出轮廓线。
下图为样例2
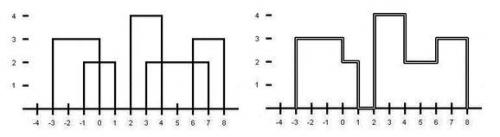
输入输出格式
输入格式:
第一行一个整数n,表示矩形个数
以下n行,每行3个整数h[i],l[i],r[i]表示第i个矩形。
输出格式:
第一行一个整数m,表示节点个数
以下m行,每行一个坐标表示轮廓线上的节点。从左到右遍历轮廓线并顺序输出节点。第一个和最后一个节点的y坐标必然为0。
输入输出样例
输出样例#1:
【样例输出1】 6 0 0 0 3 1 3 1 4 3 4 3 0 【样例输出2】 14 -3 0 -3 3 0 3 0 2 1 2 1 0 2 0 2 4 4 4 4 2 6 2 6 3 8 3 8 0
说明
【数据范围】
对于30%的数据,n<=100
对于另外30%的数据,n<=100000,1<=h[i],l[i],r[i]<=1000
对于100%的数据,1<=n<=100000,1<=h[i]<=10^9,-10^9<=l[i]<r[i]<=10^9
思路
1.扫描线:
先把每个矩形拆成两条边,一条入边,一条出边,然后按照横坐标以及高度排序,同时还需要一个堆实时记录高度,然后一遍从左到右的遍历就可以求出每个交点和交点的个数,然后即可解.
2.离散化+线段树
(贼麻烦)...
上代码
#include<bits/stdc++.h> using namespace std; const int maxn=300008; int read() { char ch=getchar();int f=1,w=0; while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch<='9'&&ch>='0'){w=w*10+ch-'0';ch=getchar();} return f*w; } struct ls{ int up; int x; int k; }l[maxn]; struct ss{ int ax; int ay; }ans[maxn*2]; int n,cnt,num; multiset<int>s; int cmp(ls i,ls j) { if(i.x!=j.x)return i.x<j.x; if(i.k!=j.k)return i.k<j.k; if(i.k==1)return i.up>j.up; if(i.k==2)return i.up<j.up; } int main(){ n=read(); for(int i=1;i<=n;i++){ int h,ll,r; h=read(),ll=read(),r=read(); l[++cnt].up=h; l[cnt].x=ll;l[cnt].k=1; l[++cnt].up=h; l[cnt].x=r,l[cnt].k=2; } sort(l+1,l+cnt+1,cmp); s.insert(0); for(int i=1;i<=cnt;i++){ int mx=*s.rbegin(); if(l[i].k==1){ if(l[i].up<=mx) s.insert(l[i].up); else{ ++num;ans[num].ax=l[i].x;ans[num].ay=mx; ++num;ans[num].ax=l[i].x;ans[num].ay=l[i].up; s.insert(l[i].up); } } if(l[i].k==2){ if(l[i].up==mx&&s.count(mx)==1){ s.erase(mx); ans[++num].ax=l[i].x; ans[num].ay=l[i].up; ans[++num].ax=l[i].x;ans[num].ay=*s.rbegin(); } else s.erase(s.find(l[i].up)); } } printf("%d ",num); for(int i=1;i<=num;i++) cout<<ans[i].ax<<' '<<ans[i].ay<<endl; return 0; }