1.0 欧拉函数的定义
1.1 欧拉函数解决的问题
任意给定正整数n,请问在小于等于n的正整数之中,有多少个与n构成互质关系?
比如说:
n=10 与n互质的数就有 : 1,3,7,9.
所以φ(10)=4;
1.2 欧拉函数的计算公式
n 需要被拆成诸如此类的形式:
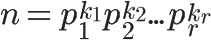
其中 p 均为质数.
然后如图,这就是欧拉函数的计算公式.
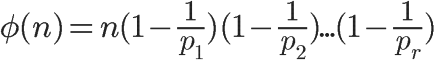
2.0 欧拉函数公式的推导
虽然公式会显得比较简单,但是欧拉函数公式需要一步一步去推导.
对此,我们需要分情况讨论.
2.1 n=1
此时 φ(1)=1 . 因为 1 与任何数都互质 (包括自身) .
2.2 n为质数
此时 φ(n)= n-1 ; 很显然.
2.3 n=p^k.
此时则 有如下公式 :

如何去思考这种情况呢 ?
易知,若 k=1 则 φ(n) = n-1;
那么,若 k=2 则在原来的 n-1 的数列中 会多了一个 k 与其不互质.
那么也就是说,我当前这个序列中,与n互质的当且仅有 p 的倍数.
所以 p^k 中含有的 p 的倍数的个数(包括自己) 即为 p^k / p ,也就是 p^(k-1).
* 2.4 n 可以写成两个互质的数的乘积.
这个证明是整个公式的关键所在.
此时即 n 可以写成
p1 X p2
此时我们则有公式 :
φ(n) = φ(p1 X p2) = φ(p1) X φ(p2)
此时我们是怎么推导出来的呢 ?
此时可以知道只有那些既满足 p1 与其互质且满足 p2 与其互质的数满足条件.
根据乘法原理.这样的数可以互相组合.那么就有 φ(a)⋅φ(b) 个.
2.5 最后公式的推导.
引理 :
任意一个大于 1 的正整数, 都可以写成诸如 p1^k1 X p2^k2 ... pi^ki 的形式.
然后根据 2.4 我们有:

再根据 2.3 我们有:

于是再化简,我们便有了 1.1 开头的式子.
2.6 例题
这里就有一道,是比较裸的欧拉函数.不过要看的出来才行.
本蒟蒻也有题解在此.
3.0 后续
这一篇只介绍了欧拉函数及欧拉函数的求法.
日后更多的性质及运用蒟蒻博主会填坑的.