跳石头
题目背景
一年一度的“跳石头”比赛又要开始了!
题目描述
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终 点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达 终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳 跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 M 块岩石(不能 移走起点和终点的岩石)。
输入输出格式
输入格式:
输入文件名为 stone.in。
输入文件第一行包含三个整数 L,N,M,分别表示起点到终点的距离,起点和终 点之间的岩石数,以及组委会至多移走的岩石数。
接下来 N 行,每行一个整数,第 i 行的整数 Di(0 < Di < L)表示第 i 块岩石与 起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同 一个位置。
输出格式:
输出文件名为 stone.out。 输出文件只包含一个整数,即最短跳跃距离的最大值。
输入输出样例
25 5 2 2 11 14 17 21
4
说明
输入输出样例 1 说明:将与起点距离为 2 和 14 的两个岩石移走后,最短的跳跃距离为 4(从与起点距离 17 的岩石跳到距离 21 的岩石,或者从距离 21 的岩石跳到终点)。
另:对于 20%的数据,0 ≤ M ≤ N ≤ 10。 对于50%的数据,0 ≤ M ≤ N ≤ 100。
对于 100%的数据,0 ≤ M ≤ N ≤ 50,000,1 ≤ L ≤ 1,000,000,000。
#include<iostream> #include<cstdio> using namespace std; int n,m,L; int a[50005],ans; int check(int x) { int last=0,cnt=0; for(int i=0;i<=n;i++) { if(a[i]-last<x){cnt+=1;continue;} last=a[i]; } if(cnt>m) return 0; return 1; } int main() { scanf("%d%d%d",&L,&n,&m); for(int i=0;i<n;i++) scanf("%d",&a[i]); a[n]=L; int r=L,l=1; while(l<=r) { int mid=(l+r)/2; if(check(mid)){ans=mid;l=mid+1;} else r=mid-1; } printf("%d ",ans); return 0; }
子串
题目背景
无
题目描述
有两个仅包含小写英文字母的字符串 A 和 B。现在要从字符串 A 中取出 k 个互不重叠的非空子串,然后把这 k 个子串按照其在字符串 A 中出现的顺序依次连接起来得到一 个新的字符串,请问有多少种方案可以使得这个新串与字符串 B 相等?注意:子串取出 的位置不同也认为是不同的方案。
输入输出格式
输入格式:
输入文件名为 substring.in。
第一行是三个正整数 n,m,k,分别表示字符串 A 的长度,字符串 B 的长度,以及问
题描述中所提到的 k,每两个整数之间用一个空格隔开。 第二行包含一个长度为 n 的字符串,表示字符串 A。 第三行包含一个长度为 m 的字符串,表示字符串 B。
输出格式:
输出文件名为 substring.out。 输出共一行,包含一个整数,表示所求方案数。由于答案可能很大,所以这里要求[b]输出答案对 1,000,000,007 取模的结果。[/b]
输入输出样例
6 3 1 aabaab aab
2
6 3 2 aabaab aab
7
6 3 3 aabaab aab
7
说明

对于第 1 组数据:1≤n≤500,1≤m≤50,k=1;
对于第 2 组至第 3 组数据:1≤n≤500,1≤m≤50,k=2; 对于第 4 组至第 5 组数据:1≤n≤500,1≤m≤50,k=m; 对于第 1 组至第 7 组数据:1≤n≤500,1≤m≤50,1≤k≤m; 对于第 1 组至第 9 组数据:1≤n≤1000,1≤m≤100,1≤k≤m; 对于所有 10 组数据:1≤n≤1000,1≤m≤200,1≤k≤m。
/* 状态f[i][j][k] 表示A串匹配到i B串匹配到j 用了k个子串 转移的话 f[i][j][k]=f[i-1][j-1][k]+f[i-1][j-1][k-1]分别表示i是不是建立了一个新的子串 当然这是我们会发现 这样的状态是默认了i用了 显然i可以不用 也就是说这样就遗漏了许多状态 我们重新定义一下他 加一维01表示i用了没用 f[i][j][k][0或1] 这样转移就要分开考虑01 f[i][j][k][0]=f[i-1][j][k][0]+f[i-1][j][k][1]因为i没有用 所以不会有新串k不变 B串也不会更新匹配j不变 f[i][j][k][1]=f[i-1][j-1][k-1][0]+f[i-1][j-1][k][1]+f[i-1][j-1][k-1][1] */ #include<iostream> #include<cstring> #include<cstdio> #define mod 1000000007 #define maxn 210 using namespace std; int n,m,p,s,f[2][maxn][maxn][2]; char A[maxn*5],B[maxn]; int main() { scanf("%d%d%d",&n,&m,&p); scanf("%s%s",A+1,B+1); for(int i=1;i<=n;i++) { f[i%2][1][1][0]=s; if(A[i]==B[1]) f[i%2][1][1][1]=1,s++; for(int j=2;j<=m;j++) for(int k=1;k<=p;k++) { f[i%2][j][k][0]=(f[(i+1)%2][j][k][0]+f[(i+1)%2][j][k][1])%mod; if(A[i]==B[j]) f[i%2][j][k][1]=((f[(i+1)%2][j-1][k-1][1]+f[(i+1)%2][j-1][k][1])%mod +f[(i+1)%2][j-1][k-1][0])%mod; } for(int j=1;j<=m;j++) for(int k=1;k<=p;k++) f[(i+1)%2][j][k][1]=0,f[(i+1)%2][j][k][0]=0; } printf("%d ",(f[n%2][m][p][0]+f[n%2][m][p][1])%mod); return 0; }
运输计划
题目背景
公元 2044 年,人类进入了宇宙纪元。
题目描述
L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条航道连通了 L 国的所有星球。
小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物
流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道 是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之 间不会产生任何干扰。
为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后, 这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的 物流公司的阶段性工作就完成了。
如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段 性工作所需要的最短时间是多少?
输入输出格式
输入格式:
输入文件名为 transport.in。
第一行包括两个正整数 n、m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。
接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和 ti,表示第
i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。
接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j个 运输计划是从 uj 号星球飞往 vj 号星球。
输出格式:
输出 共1行,包含1个整数,表示小P的物流公司完成阶段性工作所需要的最短时间。
输入输出样例
6 3 1 2 3 1 6 4 3 1 7 4 3 6 3 5 5 3 6 2 5 4 5
11
说明
所有测试数据的范围和特点如下表所示
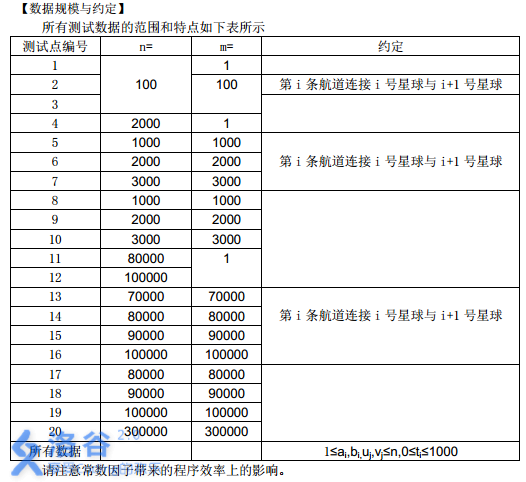
请注意常数因子带来的程序效率上的影响。

#include<iostream> #include<cstdio> #include<cstring> #define N 100001 using namespace std; int head[N<<1],t[N],f[N][25],g[N][25],sum[N],deep[N]; int n,m,x,y,z,ans,tot,cnt,tmp; struct edge { int u,to,next,dis; }e[N<<1]; inline int read() { int x=0,f=1;char c=getchar(); while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } inline void add(int u,int to,int dis) { e[++cnt].to=to;e[cnt].next=head[u];e[cnt].dis=dis;head[u]=cnt; } inline void get_fa() { for(int j=1;j<=22;j++) for(int i=1;i<=n;i++) { f[i][j]=f[f[i][j-1]][j-1]; g[i][j]=max(g[i][j-1],g[f[i][j-1]][j-1]); } } void dfs(int now,int fa,int c,int wa) { f[now][0]=fa;deep[now]=c;g[now][0]=wa;sum[now]+=wa; for(int i=head[now];i;i=e[i].next) { int v=e[i].to; if(v!=fa) { sum[v]+=sum[now]; dfs(v,now,c+1,e[i].dis); } } } int lca(int a,int b) { if(deep[a]<deep[b]) swap(a,b); int t=deep[a]-deep[b]; for(int i=0;i<=22;i++) { if(t&(1<<i)) { tmp=max(g[a][i],tmp); a=f[a][i]; } } if(a==b) return a; for(int i=21;i>=0;i--) { if(f[a][i]!=f[b][i]) { tmp=max(tmp,g[a][i]); tmp=max(tmp,g[b][i]); a=f[a][i];b=f[b][i]; } } tmp=max(tmp,max(g[a][0],g[b][0])); return f[a][0]; } int main() { n=read();m=read(); if(m==1) { for(int i=1;i<n;++i) { x=read();y=read();z=read(); add(x,y,z);add(y,x,z); } dfs(1,1,0,0);get_fa(); x=read();y=read();int L=lca(x,y); ans=sum[x]+sum[y]-2*sum[L]-tmp; printf("%d ",ans); } return 0; }
/* 首先求出每个计划的路径长度 这里写的倍增 然后二分答案 对于每个ans 统计>他的路径条数 tot 并维护与ans的最大差值 dec 并且对于每条不合法的路径维护每个点的经过次数 然后枚举点 如果经过次数==tot说明每一条不合法的都经过他 然后尝试把它建成虫洞 如果他对应边的权值>=dec 那么我们删掉它ans就合法了 关键是统计每个点在非法路径中的经过次数 : 维护sum数组 对于每个非法的路径起点a b LCA(a,b)==s sum[a]++ sum[b]++ sum[s]-=2 这样网上更新的话 经过的点的sum值都变成1 祖先s的变成0 这样就实现了sum数组的维护 */ #include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #define maxn 300100 using namespace std; int n,m,num,head[maxn],ans,inf; int fa[maxn][30],dep[maxn],dis[maxn],sum[maxn],edge[maxn]; struct node { int u,v,t,pre; }e[maxn*2]; struct Ans { int ai,bi,anc,di; }lca[maxn]; int init() { int x=0;char s=getchar(); while(s<'0'||s>'9')s=getchar(); while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} return x; } void Add(int from,int to,int dis) { num++; e[num].u=from; e[num].v=to; e[num].t=dis; e[num].pre=head[from]; head[from]=num; } void Dfs(int now,int from,int c,int Dis) { fa[now][0]=from; dep[now]=c;dis[now]=Dis; for(int i=head[now];i;i=e[i].pre) if(e[i].v!=from) { edge[e[i].v]=i; Dfs(e[i].v,now,c+1,Dis+e[i].t); } } void Get_fa() { for(int j=1;j<=16;j++) for(int i=1;i<=n;i++) fa[i][j]=fa[fa[i][j-1]][j-1]; } int Get_same(int a,int t) { for(int i=0;i<16;i++) if(t&(1<<i)) a=fa[a][i]; return a; } int LCA(int a,int b) { if(dep[a]<dep[b])swap(a,b); a=Get_same(a,dep[a]-dep[b]); if(a==b)return a; for(int i=16;i>=0;i--) if(fa[a][i]!=fa[b][i]) { a=fa[a][i]; b=fa[b][i]; } return fa[a][0]; } void Init() { n=init();m=init(); int u,v,t; for(int i=1;i<=n-1;i++) { u=init();v=init();t=init(); Add(u,v,t);Add(v,u,t); } Dfs(1,1,0,0); Get_fa(); for(int i=1;i<=m;i++) { lca[i].ai=init();lca[i].bi=init(); lca[i].anc=LCA(lca[i].ai,lca[i].bi); lca[i].di=dis[lca[i].ai]+dis[lca[i].bi]-2*dis[lca[i].anc]; inf=max(inf,lca[i].di); } } void Up_sum(int now,int from) { for(int i=head[now];i;i=e[i].pre) if(e[i].v!=from) { Up_sum(e[i].v,now); sum[now]+=sum[e[i].v]; } } int Judge(int x) { memset(sum,0,sizeof(sum)); int tot=0,dec=0; for(int i=1;i<=m;i++) if(lca[i].di>x)//非法路径 { tot++; dec=max(dec,lca[i].di-x);//最长非法路径与ans差值 sum[lca[i].ai]++; sum[lca[i].bi]++; sum[lca[i].anc]-=2; } Up_sum(1,1);//更新sum数组 for(int i=1;i<=n;i++) if(tot==sum[i]&&e[edge[i]].t>=dec)//删掉edge[i]这条边之后答案合法了 return 1; return 0; } void Solve()//二分答案 { int l=0,r=inf; while(l<=r) { int mid=(l+r)/2; int tmp=Judge(mid); if(tmp==1) { r=mid-1; ans=mid; } else l=mid+1; } } void Printf() { printf("%d ",ans); } int main() { Init(); Solve(); Printf(); return 0; }

/* 实在羞于打上自己的分数:10+10+20=40; 试问一下,这要是放在考场上呢?!读错题,没考虑全面是理由吗!!! T1 10分!!以前还做过。T2连hash暴力都写挂...我不想多数什么,dp方程没有耐心推,暴力没耐心调。连个小数据都舍不得造! 很基础的东西都忘了怎么写! 不管怎样,这就noip了,希望自己有数,提高效率!!!耐心 。 */
