转载请引用:一个故事讲清楚NIO
假设某银行只有10个职员。该银行的业务流程分为以下4个步骤:
1) 顾客填申请表(5分钟);
2) 职员审核(1分钟);
3) 职员叫保安去金库取钱(3分钟);
4) 职员打印票据,并将钱和票据返回给顾客(1分钟)。
我们看看银行不同的工作方式对其工作效率到底有何影响。
1 BIO方式
每来一个顾客,马上由一位职员来接待处理,并且这个职员需要负责以上4个完整流程。当超过10个顾客时,剩余的顾客需要排队等候。
我们算算这个银行一个小时到底能处理多少顾客?一个职员处理一个顾客需要10分钟(5+1+3+1)时间,一个小时(60分钟)能处理6个顾客,一共10个职员,那就是只能处理60个顾客。
可以看到银行职员的工作状态并不饱和,比如在第1步,其实是处于等待中。
这种工作其实就是BIO,每次来一个请求(顾客),就分配到线程池中由一个线程(职员)处理,如果超出了线程池的最大上限(10个),就扔到队列等待 。
2 NIO方式
如何提高银行的吞吐量呢?
思路:分而治之,将任务拆分开来,由专门的人负责专门的任务。
具体来讲,银行专门指派一名职员A,A的工作就是每当有顾客到银行,他就递上表格让顾客填写,每当有顾客填好表后,A就将其随机指派给剩余的9名职员完成后续步骤。
我们计算下这种工作方式下银行一个小时到底能处理多少顾客?
假设顾客非常多,职员A的工作处于饱和中,他不断的将填好表的顾客带到柜台处理,柜台一个职员5分钟能处理完一个顾客,一个小时9名职员能处理:9*(60/5)=108。
可见工作方式的转变能带来效率的极大提升。
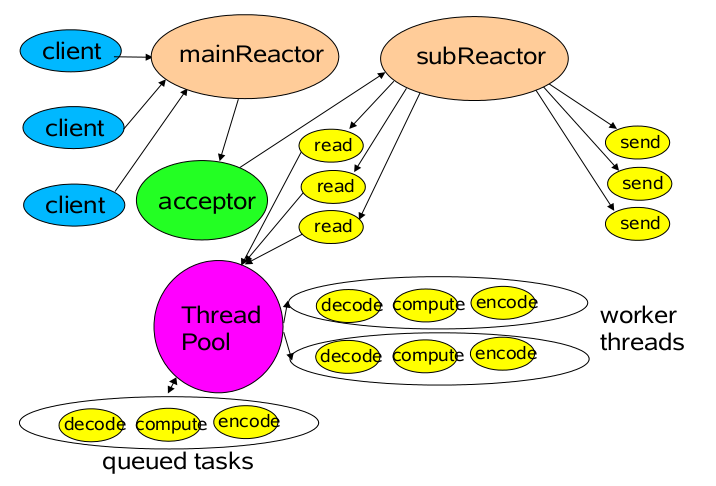
这种工作方式其实就NIO的思路。下图是非常经典的NIO说明图,mainReactor线程负责监听server socket,accept新连接,并将建立的socket分派给subReactor;subReactor可以是一个线程,也可以是线程池(一般可以设置为CPU核数),负责多路分离已连接的socket,读写网络数据,这里的读写网络数据可类比顾客填表这一耗时动作,对具体的业务处理功能,其扔给worker线程池完成。
可以看到典型NIO有三类线程,分别是mainReactor线程、subReactor线程、work线程。不同的线程干专业的事情,最终每个线程都没空着,系统的吞吐量自然就上去了。
3 异步方式
第二种工作方式有没有什么可以提高的地方呢?
仔细查看可发现第3步骤这3分钟柜台职员是在等待中度过的,那怎么能让柜台职员保持满负荷呢?
还是分而治之的思路,指派1个职员B来专门负责第3步骤。每当柜台员工完成第2步时,就通知职员B来负责与保安沟通取钱。这时候柜台员工可以继续处理下一个顾客。当职员B拿到钱之后,他会怎么办呢?他会通知顾客钱已经到柜台了,让顾客重新排队处理,当柜台职员再次服务该顾客时,发现该顾客前3步已经完成,直接执行第4步即可。
我们可以算算通过这种方法,银行的吞吐量能提高到多少。
假设职员B的工作非常饱和,柜台一个职员现在2分钟能处理完一个顾客,一个小时8名职员能处理:8*(60/2)=240。
在当今web服务中,经常需要通过RPC或者Http等方式调用第三方服务,这里对应的就是第3步,如果这步耗时较长,通过异步方式将能极大降低资源使用率。
jetty Continuations 就实现了上述异步方式,有兴趣的同学可以去尝试下(http://wiki.eclipse.org/Jetty/Feature/Continuations)。
NIO+异步的方式能让少量的线程(资源)做大量的事情,这适用于很多应用场景,比如代理服务、api服务、长连接服务等等,这些应用如果用同步方式将耗费大量机器资源。尽管NIO+异步能提高系统吞吐量,但其并不能让一个请求的等待时间下降,相反可能会增加等待时间。
4 小结
总结就一句:“分而治之,将任务拆分开来,由专门的人负责专门的任务”,这不仅在计算机领域生效,在整个社会领域都生效。