计算第n个斐波那契数

方法一：传统递归法

时间复杂度O(2^n)，空间复杂度O(n)

计算Fibonacci(10)十次平均用时0.0003s    计算Fibonacci(100)单次用时大于1min

时间复杂度极高，当n>35左右时间已经无法接受

def Fibonacci(n):
    if n == 1 or n == 2:
        return 1
    return Fibonacci(n - 1) + Fibonacci(n - 2)

方法二：动态规划法

时间复杂度O(n)，空间复杂度O(1)

计算Fibonacci(10)十次平均用时小于0.00001s    计算Fibonacci(100)十次平均0.0001s    计算Fibonacci(10000)十次平均0.008s    计算Fibonacci(1000000)十次平均9.525s

def Fibonacci(n):
    current, pre = 1, 0
    for i in range(n - 1):
        current, pre, = current + pre, current
    return current

方法三：通项公式法

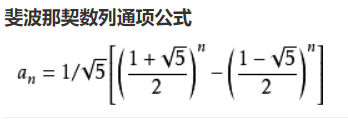
时间复杂度O(log n)，空间复杂度O(1)，通项公式法的时间复杂度不是O(1)，这是因为计算n次幂不能做到O(1)时间复杂度，使用快速幂算法可以做到(log n)时间复杂度

计算Fibonacci(10)十次平均用时小于0.00001s    计算Fibonacci(100)十次平均用时小于0.00001s

计算Fibonacci(10000)数字太大，出现OverFlow错误    计算Fibonacci(1000000)：数字太大，出现OverFlow错误

 由于开方和四舍五入存在精度误差，经过测试，使用通项公式法计算斐波那契数列在第71项时开始出现精度导致的计算错误。

根据测试可知，通项公式法只在理论上可行，没有操作性。

def Fibonacci(n):
    sqrt5 = 5 ** 0.5
    ans = (((1 + sqrt5) / 2) ** n - (((1 - sqrt5) / 2) ** n)) / sqrt5
    return round(ans)

方法四：矩阵法

主要原理是以下公式和快速幂算法

这种算法是求任意线性常系数递归递推关系的任意项的通用解法，而且通常也是最优解

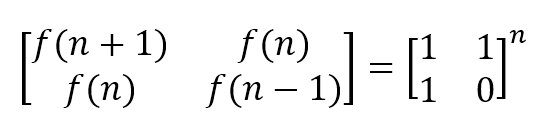
时间复杂度O(log n)，空间复杂度O(log n)（由递归深度决定）

计算Fibonacci(10)十次平均用时0.0002s    计算Fibonacci(100)十次平均0.0003s    计算Fibonacci(10000)十次平均0.0008s    计算Fibonacci(1000000)十次平均0.184s

可以看出当n较大时，矩阵法明显优于动态规划法

另外，在这个方法中，使用了Strassen算法算法计算矩阵的乘法（该算法可以使得两个大小为n的方朕相乘的时间复杂度由传统的O(n ^ 3)下降到O(n ^ 2.81)）

同时在快速幂算法中使用了一定的位运算技巧以达到最优化的性能

（笔者同时测试了把快速幂的递归算法换成非递归算法，非递归算法的时间大概是递归算法的两倍）

def Matrix_Multiply(matrix1, matrix2):
    a, b, c, d = matrix1[0][0], matrix1[0][1], matrix1[1][0], matrix1[1][1]
    e, f, g, h = matrix2[0][0], matrix2[0][1], matrix2[1][0], matrix2[1][1]
    p1 = a * (f - h)
    p2 = (a + b) * h
    p3 = (c + d) * e
    p4 = d * (g - e)
    p5 = (a + d) * (e + h)
    p6 = (b - d) * (g + h)
    p7 = (a - c) * (e + f)
    r = p5 + p4 - p2 + p6
    s = p1 + p2
    t = p3 + p4
    u = p5 + p1 - p3 - p7
    return [[r, s], [t, u]]


def Matrix_Quick_Pow(matrix, p):
    if p == 1:
        return matrix
    if p & 1:
        temp = Matrix_Quick_Pow(matrix, p >> 1)
        return Matrix_Multiply(Matrix_Multiply(temp, temp), matrix)
    else:
        tmp = Matrix_Quick_Pow(matrix, p >> 1)
        return Matrix_Multiply(tmp, tmp)


def Fibonacci(n):
    matrix = [[1, 1], [1, 0]]
    return Matrix_Quick_Pow(matrix, n)[0][1]