soeasy的键盘鼠标事件

在web自动化中，我们可能会遇到需要通过键盘或者鼠标去操作某些元素，那么我们就需要用到键盘事件和鼠标事件了，今天对键盘和鼠标操作进行一个总结

鼠标事件

　　鼠标事件需要引入ActionChains类，查看源码可以看到ActionChains初始化需要传递的是当前会话

　　

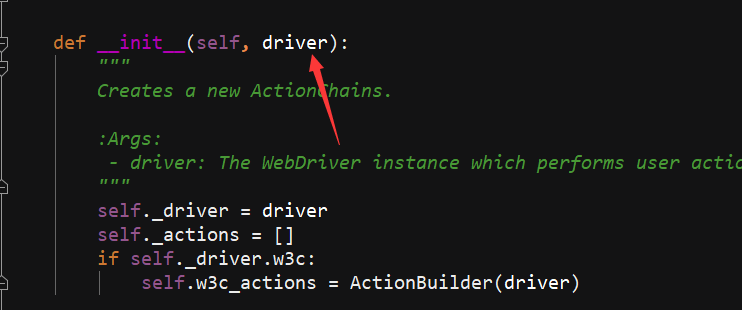
 鼠标操作的步骤：

　　1、储存鼠标操作

　　2、执行操作，利用perform()方法执行操作

常用的鼠标操作有：

　　move_to_element     悬浮

　　drag_and_drop         拖拽操作

　　double_click              双击

　　context_click             右击

具体需要什么，可以查看源码，很丰富，很详细哈。。。

举个栗子：

　　百度首页--高级搜索

 示例代码：

from selenium import webdriver
from selenium.webdriver.support.wait import WebDriverWait    
from selenium.webdriver.support import expected_conditions as EC
from selenium.webdriver.common.by import By
from selenium.webdriver.common.action_chains import ActionChains


dr = webdriver.Chrome()
dr.get("http://www.baidu.com")
col = (By.XPATH, '//div[@id="u1"]//a[@class="pf"]')   # 设置的元素定位
WebDriverWait(dr, 10, 0.5).until(EC.visibility_of_element_located(col))   # 显性等待设置按钮元素存在
el = dr.find_element(*col)
ActionChains(dr).move_to_element(el).perform()    # 鼠标悬浮至设置按钮
co = (By.XPATH, '//a[text()="高级搜索"]')
WebDriverWait(dr, 10, 0.5).until(EC.visibility_of_element_located(co))
dr.find_element(*co).click()    # 点击高级搜索

键盘事件

　　键盘事件我们一般很少用，还是总结下吧

键盘事件主要是引用Keys这个类

组合键：

　　send_keys(Keys.CONTROL,'a')        全选

　　send_keys(Keys.CONTROL,'c')        复制

　　send_keys(Keys.CONTROL,'v')　　 粘贴

　　send_keys(Keys.CONTROL,'x')　　 剪切

非组合键：

　　回车： Keys.ENTER

　　删除：Keys.BACK_SPACE

　　空格：Keys.SPACE

　　制表：Keys.TAB

　　刷新：Keys.F5

举个栗子

　　百度首页用回车键代替搜索按钮

from selenium import webdriver
from selenium.webdriver.common.keys import Keys


dr = webdriver.Chrome()
dr.get("http://www.baidu.com")
dr.implicitly_wait(3)
dr.find_element(By.ID, "kw").send_keys("腾讯", Keys.ENTER)

以上就是总结的键盘、鼠标事件