k近邻算法(knn)的c语言实现

　　最近在看knn算法，顺便敲敲代码。

　

　　knn属于数据挖掘的分类算法。基本思想是在距离空间里，如果一个样本的最接近的k个邻居里，绝大多数属于某个类别，则该样本也属于这个类别。俗话叫，“随大流”。

　　简单来说，KNN可以看成：有那么一堆你已经知道分类的数据，然后当一个新的数据进入的时候，就开始跟训练里的每个点求距离，然后挑出离这个数据最近的K个点，看看这K个点属于什么类型，然后用少数服从多数的原则，给新数据归类。

　　该算法的示意图，简单明了：

　　

　　　　下面的算法步骤取自于百度文库（文库是一个好东西），代码是参照这个思路实现的：

　　 

　　code:

#include<stdio.h>
#include<math.h>
#include<stdlib.h>

#define K 3 //近邻数k
typedef float type;

//动态创建二维数组
type **createarray(int n,int m)
{
    int i;
    type **array;
    array=(type **)malloc(n*sizeof(type *));
    array[0]=(type *)malloc(n*m*sizeof(type));
    for(i=1;i<n;i++) array[i]=array[i-1]+m;
    return array;
}
//读取数据，要求首行格式为 N=数据量,D=维数
void loaddata(int *n,int *d,type ***array,type ***karray)
{
    int i,j;
    FILE *fp;
    if((fp=fopen("data.txt","r"))==NULL)    fprintf(stderr,"can not open data.txt!\n");
    if(fscanf(fp,"N=%d,D=%d",n,d)!=2)    fprintf(stderr,"reading error!\n");
    *array=createarray(*n,*d);
    *karray=createarray(2,K);

    for(i=0;i<*n;i++)
        for(j=0;j<*d;j++)
            fscanf(fp,"%f",&(*array)[i][j]);    //读取数据

    for(i=0;i<2;i++)
        for(j=0;j<K;j++)
            (*karray)[i][j]=9999.0;    //默认的最大值
    if(fclose(fp))    fprintf(stderr,"can not close data.txt");
}
//计算欧氏距离
type computedistance(int n,type *avector,type *bvector)
{
    int i;
    type dist=0.0;
    for(i=0;i<n;i++)
        dist+=pow(avector[i]-bvector[i],2);
    return sqrt(dist);
}
//冒泡排序
void bublesort(int n,type **a,int choice)
{
    int i,j;
    type k;
    for(j=0;j<n;j++)
        for(i=0;i<n-j-1;i++){
            if(0==choice){
                if(a[0][i]>a[0][i+1]){
                    k=a[0][i];
                    a[0][i]=a[0][i+1];
                    a[0][i+1]=k;
                    k=a[1][i];
                    a[1][i]=a[1][i+1];
                    a[1][i+1]=k;
                }
            }
            else if(1==choice){
                if(a[1][i]>a[1][i+1]){
                    k=a[0][i];
                    a[0][i]=a[0][i+1];
                    a[0][i+1]=k;
                    k=a[1][i];
                    a[1][i]=a[1][i+1];
                    a[1][i+1]=k;
                }
            }
        }
}
//统计有序表中的元素个数
type orderedlist(int n,type *list)
{
    int i,count=1,maxcount=1;
    type value;
    for(i=0;i<(n-1);i++) {
        if(list[i]!=list[i+1]) {
            //printf("count of %d is value %d\n",list[i],count);
            if(count>maxcount){
                maxcount=count;
                value=list[i];
                count=1;
            }
        }
        else
            count++;
    }
    if(count>maxcount){
            maxcount=count;
            value=list[n-1];
    }
    //printf("value %f has a Maxcount:%d\n",value,maxcount);
    return value;
}

int main()
{
    int i,j,k;
    int D,N;    //维度，数据量
    type **array=NULL;  //数据数组
    type **karray=NULL; //  K近邻点的距离及其标签
    type *testdata; //测试数据
    type dist,maxdist;

    loaddata(&N,&D,&array,&karray);
    testdata=(type *)malloc((D-1)*sizeof(type));
    printf("input test data containing %d numbers:\n",D-1);
    for(i=0;i<(D-1);i++)    scanf("%f",&testdata[i]);

    while(1){
    for(i=0;i<K;i++){
        if(K>N) exit(-1);
        karray[0][i]=computedistance(D-1,testdata,array[i]);
        karray[1][i]=array[i][D-1];
        //printf("first karray:%6.2f  %6.0f\n",karray[0][i],karray[1][i]);
    }

    bublesort(K,karray,0);
    //for(i=0;i<K;i++)    printf("after bublesort in first karray:%6.2f  %6.0f\n",karray[0][i],karray[1][i]);
    maxdist=karray[0][K-1]; //初始化k近邻数组的距离最大值

    for(i=K;i<N;i++){
        dist=computedistance(D-1,testdata,array[i]);
        if(dist<maxdist)
            for(j=0;j<K;j++){
                if(dist<karray[0][j]){
                    for(k=K-1;k>j;k--){ //j后元素复制到后一位，为插入做准备
                        karray[0][k]=karray[0][k-1];
                        karray[1][k]=karray[1][k-1];
                    }
                    karray[0][j]=dist;  //插入到j位置
                    karray[1][j]=array[i][D-1];
                    //printf("i:%d  karray:%6.2f %6.0f\n",i,karray[0][j],karray[1][j]);
                    break;  //不比较karray后续元素
                }
            }
        maxdist=karray[0][K-1];
        //printf("i:%d  maxdist:%6.2f\n",i,maxdist);
    }
    //for(i=0;i<K;i++)    printf("karray：%6.2f  %6.0f\n",karray[0][i],karray[1][i]);
    bublesort(K,karray,1);
    //for(i=0;i<K;i++)    printf("after bublesort in karray：%6.2f  %6.0f\n",karray[0][i],karray[1][i]);
    printf("\nThe data has a tag: %.0f\n\n",orderedlist(K,karray[1]));

    printf("input test data containing %d numbers:\n",D-1);
    for(i=0;i<(D-1);i++)    scanf("%f",&testdata[i]);
    }
    return 0;
}

　　实验：

　　训练数据data.txt：

　　N=6,D=9
　　1.0 1.1 1.2 2.1 0.3 2.3 1.4 0.5 1
　　1.7 1.2 1.4 2.0 0.2 2.5 1.2 0.8 1
　　1.2 1.8 1.6 2.5 0.1 2.2 1.8 0.2 1
　　1.9 2.1 6.2 1.1 0.9 3.3 2.4 5.5 0
　　1.0 0.8 1.6 2.1 0.2 2.3 1.6 0.5 1
　　1.6 2.1 5.2 1.1 0.8 3.6 2.4 4.5 0

　　预测数据：

　　1.0 1.1 1.2 2.1 0.3 2.3 1.4 0.5

　　1.7 1.2 1.4 2.0 0.2 2.5 1.2 0.8

　　1.2 1.8 1.6 2.5 0.1 2.2 1.8 0.2

　　1.9 2.1 6.2 1.1 0.9 3.3 2.4 5.5

　　1.0 0.8 1.6 2.1 0.2 2.3 1.6 0.5

　　1.6 2.1 5.2 1.1 0.8 3.6 2.4 4.5 

 　　

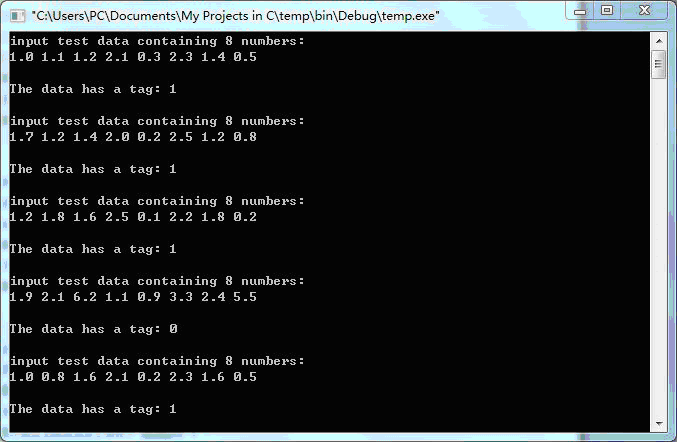
　　程序测试的结果：

　　1.0 1.1 1.2 2.1 0.3 2.3 1.4 0.5 类别为: 1

　　1.7 1.2 1.4 2.0 0.2 2.5 1.2 0.8 类别为: 1

　　1.2 1.8 1.6 2.5 0.1 2.2 1.8 0.2 类别为: 1

　　1.9 2.1 6.2 1.1 0.9 3.3 2.4 5.5 类别为: 0

　　1.0 0.8 1.6 2.1 0.2 2.3 1.6 0.5 类别为: 1

　　1.6 2.1 5.2 1.1 0.8 3.6 2.4 4.5 类别为: 0

　　实验截图：