现在我才明白,自己之前做的最短路的题是有多么垃圾。



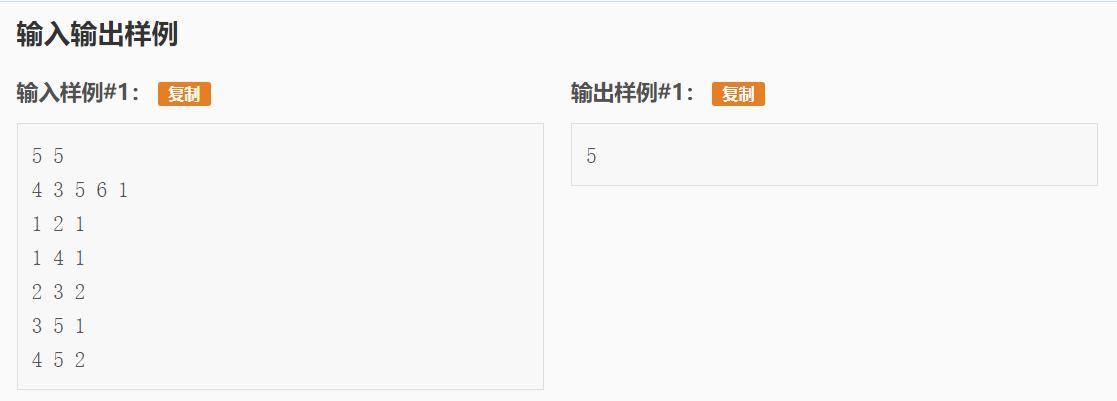

题面很长,但其实就说的是一个中间商赚差价的故事。图论的题目一般来说建图往往是核心,而这道题的巧妙之处是在于它需要建两个图:正图和反图,正图是1-n的路径,而反图则是从n反推到1。
题目要求我们去的在某个城市买,回来又在某个城市卖出,可以维护两个值,卖出的最大价格最大mx和最小价格mi,对于可以相互到达的城市来说,最小值和最大值都是一样的。
所以先从1-n跑spfa,求出买入商品的最小值,又从n-1在反图上跑spfa,求出回来时卖出的最大值。最后for一遍所有的点,找到最大差价即可。
其实想一想还是非常简单的。代码如下(参考了蒋神的代码和网上的题解):
#include<bits/stdc++.h> using namespace std; const int maxn=1e6+7; const int INF=0x3f3f3f3f; struct node{ int nxt; int to; }edge[maxn*2]; struct node1{ int nxt; int to; }edge1[maxn*2]; int x,y,z; int n,m; int head[maxn],cnt; int val[maxn]; int mi[maxn],mx[maxn]; bool vis[maxn]; void add(int x,int y){ edge[++cnt].nxt=head[x]; edge[cnt].to=y; head[x]=cnt; } int head2[maxn],cnt2; void add2(int x,int y){ edge1[++cnt2].nxt=head2[x]; edge1[cnt2].to=y; head2[x]=cnt2; } queue<int> q; void spfa1(){ for(int i=1;i<=n;i++){ mi[i]=INF; vis[i]=false; } mi[1]=val[1]; q.push(1); vis[1]=true; while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head[u];i;i=edge[i].nxt){ int v=edge[i].to; if(mi[v]>min(mi[u],val[v])){ mi[v]=min(mi[u],val[v]); if(!vis[v]){ q.push(v); vis[v]=true; } } } } } void spfa2(){ for(int i=1;i<=n;i++){ mx[i]=-INF; vis[i]=false; } mx[n]=val[n]; q.push(n); vis[n]=true; while(!q.empty()){ int u=q.front(); q.pop(); for(int i=head2[u];i;i=edge1[i].nxt){ int v=edge1[i].to; if(mx[v]<max(mx[u],val[v])){ mx[v]=max(mx[u],val[v]); if(!vis[v]){ q.push(v); vis[v]=true; } } } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ scanf("%d",&val[i]); } for(int i=1;i<=m;i++){ scanf("%d%d%d",&x,&y,&z); if(z==1){ add(x,y); add2(y,x); } else{ add(x,y); add(y,x); add2(x,y); add2(y,x); } } spfa1(); spfa2(); int ans=0; for(int i=1;i<=n;i++){ ans=max(ans,mx[i]-mi[i]); } printf("%d ",ans); return 0; }